＜基本粒子の運動状態の一考察；素光子説＞

　

　　１９７３年〜２０１４年３月７日更新

　　岡山 洋二 ＜jh6noa@mua.biglobe.ne.jp＞

　

　

（要約）

　核反応による物質の質量欠損や２個の光子の正面衝突による正粒子と反粒子の

対生成や正粒子と反粒子の対消滅による２個の光子の発生の事実やエネルギーと

質量の等価式；Ｅ＝ｍｃ^2を考慮する事により、１９７３年に、「物質は光が固

まったものではないか！？」という素朴な発想を思い付き、今日まで、この考え

の妥当性を考察してきた。

光を光子という下部構造を有しない素粒子の概念のままで論理展開を行おうとす

ると、多様な物質を表現する自由度が不足し、直ちに困難に陥ると判断し、光子

に下部構造を想定し、その構成要素としての真の素粒子である基本粒子を素光子

と名付け、素光子同士が束縛状態となり、光速では運動できない状態の素光子を

素量子（質量を有する全ての物質の構成要素）と名付けた。

なお、一時期、光速を越えるとの実験結果で騒がれたニュートリノは、光子より

も小さい素光子の集団であると推測している。

量子力学を始め現行の物理理論の基本概念であるエネルギーの連続性を再検討し

た結果、エネルギーの不連続性の可能性を見い出し、不確定性原理を考慮して、

エネルギーの最小単位（エネルギー素量ε）を、作用素量であるプランク定数ｈ

（ｊ・ｓ）を考慮してε＝ｈ（ｊ）と推定し、これを担うに相応しい素粒子とし

て素光子を充て、これを素光子の固有エネルギーと想定した。

真の素粒子と位置付ける素光子及び素量子の基本性質として必要と考える、固有

エネルギー不変の原理を課す事により、光を含めた全ての物質の、時間発展に限

らず座標変換に於けるエネルギー保存則が成立する事となり、これは現行の物理

理論に対する最大の優位点と考えた。

素量子の運動状態に於ける全エネルギー（質量エネルギー＋運動エネルギー）を

不変とする条件の基で素量子の運動状態式を求めてみたが、この方程式の両辺に

ローレンツ因子γを付加した方程式が自由粒子の相対論的ハミルトニアンである

事が解り、素量子の運動状態式が力学理論の基本方程式である事の目処が付いた

ものと考え、この方程式を自由粒子の素光子説的ハミルトニアンと呼ぶ事とした。

この方程式の一つの解として、物質の運動速度が光速に近付くに連れて、速度の

加算が頭打ち状態になる事を認め、この現象を現行の理論に適用する際に思い付

いた現行の速度の線形の概念を非線形に変更する事で、座標変換に於いて、光速

不変性を保ちながら絶対に不可能と考えられている時間と空間を不変に保つ事を

可能とする非線形速度の性質を設定する事が可能である事を証明する事が出来た。

アハラノフ・ボーム効果にてベクトル・ポテンシャルの実在性が予言されていた

が、外村彰博士の実証実験にて証明された事により、ベクトル・ポテンシャルと

素光子とは概念上は異なるが同一の物質であり、素光子の実在性が証明されたも

のと判断した。

宇宙に均等に分布して光速で自由に運動している素光子の集団（自由素光子場）

の存在を推定し、これをゼロ点エネルギーや真空エネルギーに対比した。

宇宙空間に慣性運動中の任意の物体が存在する場合に、周囲の自由素光子場から

物体へ加えられる合力はゼロ（慣性運動と慣性力の本質）となるが、外力が物体

に加えられて加速運動が生じると、加速方向から衝突する自由素光子の運動量が

増加し、逆方向から衝突する自由素光子の運動量が減少する事から、この合力が

加速運動に抵抗する力となり、これが慣性力として観測されるものと推測した。

更に、宇宙空間に２つの物体が存在する場合は、各々の物体による自由素光子の

運動が遮蔽される結果、物体間の自由素光子場の密度が低下する事により、物体

同士を接近させる方向に合力が働く事となり、これを万有引力として観測する事

となるものと推測した。（Le Sageの重力理論による重力の発生機序）

ところで、非線形速度の概念から類推して非線形距離の概念を創案し、この距離

の性質である遠くの空間ほど相対的に収縮している事による静的な空間の膨張に

依るハッブルが発見した遠くの天体の光ほど赤方偏移率が増加して観測されると

いう天体観測結果を説明する定常宇宙論を提案した。

更に、四次元ユークリッド空間の特異性であるドナルドソンの定理は、非線形の

距離の性質を数学上で表現したものと判断し、理論上のドナルドソンの定理及び

天体観測上のハッブルの法則という理論と実証の両面、更に、Le Sageの重力理論

の妥当性から宇宙は歪みが無い四次元ユークリッド空間と結論し、ペレリマンに

よるポアンカレ予想の証明も加わる事で、四次元超球の表面を我々が感知可能な

三次元ユークリッド空間という有限ではあるが果ての無い、光速で常に運動して

いる自由素光子場の定常的な循環を可能とする新しい定常有限宇宙論のモデルを

提案した。

自由素光子場に存在する光速より遅い速度でしか運動できない素量子の集合体で

ある質量を有する電子や陽子や中性子は、素光子場の密度に比例する素光子圧で

自然崩壊を免れているものと推測し、星の内部では素光子圧が低下することで、

物質の自然崩壊が生じている事を推測した。

この結果、星の質量には上限が有り、上限値を越えると超新星爆発が生じる事を

推測した。

また、量子力学の基本概念の量子の奇妙な振る舞いを、古典粒子が自由素光子場

（ボームの量子ポテンシャルに相当）を加速度運動する際に受ける慣性力による

二次的な現象ではないかと推測した。

更に、現行の電磁気現象の電荷のモデルに代わる荷電粒子の周囲を旋回している

素光子のモデルを提案し、平行なスピン状態の電子間に引力が生じる事により、

クーパー対を容易に構成する事が可能となり、高温超伝導技術の発展に寄与する

可能性を論じ、更に、核子間の引力もクーパー対と同様な機序にて説明可能とな

れば、現行の核力を説明する強い力とは異なる見地から、常温核融合を実現する

突破口が見出される可能性を推論した。

また、中性子も陽子と電子のクーパー対と同じ機序で結合しているが、結合力が

弱いために、軽い電子が容易に結合状態から離れ易い状態となり、これが中性子

のβ崩壊を生じる原因（弱い力の説明）では無いかと推測した。

以上の様に、電磁気力を始めとして、重力、強い力、更に弱い力に至るまで、全

ての基本的な力を素光子の働きのみで説明可能とする究極のシンプル性を有する

万物理論（素光子一元説）についても言及した。

これまでの自然科学の進歩の過程に於ける多くの経験則により、自然の仕組みを

説明する上で、最も単純な仮定で最も多くの現象を説明する理論がより優れてい

る（真理に近付いている。）と考えられており、これからの自然科学の発展にも

この経験則が中心的な役割を果たしていく事は間違いないものと考える。

素光子説は、唯一の基本粒子のみで宇宙の森羅万象を説明する事を最終目的とし

ており、素光子説より単純な理論は論理的には不可能であり、最終理論の最有力

候補と考えている。

この理論の正否は、我々が経験し得る全ての現象を素光子説のみで説明できるか

否かに掛かっている事になる。

これ迄の長年の考察した内容は、無意識の内にこれを検証する過程であり、今後

は自然科学の各分野の専門家による徹底的な検証を期待するところである。

　

　

Ａ節（はじめに）

　私は、物理学も数学も専門外の素人であり、学生時代に好きな物理学を楽しん

でいた際に思い付いた「物質とは光が固まったものではないか！？」という素朴

な発想を今日まで暖め、時折考えた事を徒然に書き記して幾度となく修正、廃棄、

加筆を繰り返してきたものがこのレポートであり、出来るだけ多くの方々の忌憚

のない批評を切に希望します。

　

　量子力学の基本概念であるエネルギーの量子化が本質的に意味するところは、

物質とは際限なく分割可能なもの（無限小という抽象的な数学の概念）ではなく、

これ以上分割不能な基本粒子（自然の最小単位という具象的な物理学の概念）を

想定すべき事を暗に要請しているものと考える。

そこで、自然現象の本質を考える上で、先ず万物の基本的な構成要素であるべき

基本粒子についての適切な仮定に基づいた十分な考察が不可欠であろう。

今回、ある一つの基本粒子像を想定し、その粒子の振る舞いを特殊相対性理論を

始め現行の全ての主要な物理理論との間での整合性を考慮して論述できる可能性

を検討してみたので報告する。

　

　

Ｂ節（素光子及び素量子の基本性質）

　素光子及び素量子に関する基本的な性質を推定し仮定する。

　

B節＞光子のエネルギーの不連続性の証明

　光子のエネルギーＥは、Ｅ＝ｈν（ｈ；プランク定数、ν；光子の振動数）と

して表現されるが、ハイゼンベルクの不確定原理を考慮して、プランク定数に現

れるエネルギー（ｈ／ｓ）をエネルギー素量εと仮定し、このエネルギーを担う

基本粒子の存在を想定して、それを素光子と呼ぶ事にする。

尚、光子の運動量；ｐ＝ｈν／ｃから類推して、素光子の運動量；ｐ0＝ｈ／ｃと

推定すると、素光子の固有エネルギーε（ｈ／ｓ）と共に、時間発展並びに座標

変換に於いても一定の普遍量という事になる。

　

光子の振動数νは一見すると連続した実数を取り得る様に思われるが、自然現象

としての振動を考えると、中途半端な振動など存在せず、必ず１周期分の完全な

状態の振動のみが存在し、それを１回の振動として計数されるべきであり、本来

の振動数は、相互作用の始めから終了までの経過時間（相互作用時間）で、その

間に観測される振動の回数（自然数）を除する操作を行う事で算出される物理量

である事を再確認する必要がある。

単位時間当たりの振動の回数νが実数を取り得る原因は、電子から光が放射され

る時間（相互作用時間と一致）で、時間内にカウントされる振動の回数を除して

単位時間当たりの振動の回数に換算する際の人為的な算術上の見かけの実数化で

あり、これをもって自然現象としての光子の振動数が連続した実数値を取り得る

とする従来の考えは早計であり、誤った判断であると考えざるを得ない。

この事柄を以下で論理的に証明する事とする。

　

先ず、光子の概念の中心となるエネルギー式（Ｅ＝ｈν）について考察する。

光子のエネルギーが振動数のみに依存している事は、光のもう一つのモデルであ

る電磁波のエネルギーが電子から放射される光の放射時間に依存している事を考

えると大変不可解である。

ここで、その原因を論理的に検討する事とする。

　

電磁波のエネルギーＥは、e（１波長分のエネルギー）、ν（周波数）、

Ｔ（電子よりの放射時間）の各要素が決まれば、一意的に決定される。

一個の光子に対応する一個の電磁波を構成している波の総数Ｎは、

　

Ｎ=νＴ

　

よって、

　

（エネルギー；Ｅ）＝（波の総数；Ｎ）×（１波長分のエネルギー；ｅ）

　

から、

　

Ｅ＝Ｎ・e＝νＴ・e＝（Ｔ・e）ν

　

となり、これが光子のエネルギー（Ｅ＝ｈν）と同じであるので、

　

（Ｔ・e）ν＝ｈν

∴Ｔ・e＝ｈ　・・・（Ａ）

　

となり、Ｔ（放射時間）とe（電磁波の１波長分のエネルギー）の積が、プランク

定数である一定値ｈを取る事が必要となる。

ところが、Ｔとeの間に逆比例となる事実は無い為に、Ｔ（電子よりの放射時間）

とe（１波長分のエネルギー）は共に一定値を取る事が必要となる。

この推論は、これまでの観測事実と一致する。

以上の結果を纏めると、光子のエネルギーがｈνで表現できる為には、電子から

の光の放射時間が一定値を取らなければならないという事になる。

また、e（電磁波の１波長分のエネルギー）が一定値を取らなければならない事は、

光子の場合に限らず電磁波の場合も同様であるが、この事が意味する事は、重ね

合わせの無い１個の光子や電磁波の振幅は、振動数（周波数）に依らず全て同一

であるという事である。

ここで、一つ疑問な点は、原子に捕捉されている電子以外の自由電子や原子核の

核子（特に陽子）から光が放射される場合に、一波長分の波のエネルギーが常に

一定値であるｅとなっているのか否かという事であるが、別の機会に検討したい。

　

尚、式Ａの意味する事は、プランク定数は電磁波の一波長分の波のエネルギーと

原子核に捕捉されている電子から放射される光の放射時間の積ということから、

光のエネルギーを導出する際に必須な放射時間という因子が、光子のエネルギー

を表すｈνに現れない事が本質的に意味している事は、放射時間が一定値という

事でプランク定数に既に織り込み済みという事となり、自然の最も基本的な定数

の一つと位置づけられているプランク定数は、実は極めて限定された自然現象を

基に導き出された普遍量という事で、些か色褪せた感も否めないが、その本質的

に意味することが非常に重要である事には変わりがないと考える。

つまり、（エネルギー）×（時間）という次元を持つプランク定数が自然の最小

の現象を研究する量子力学に常に登場する事の意味は、この時間の単位を単なる

単位合わせの意味しか持ち得ないと解釈すると、このエネルギーが自然の最小の

事象を演出している最小のエネルギー単位を示唆していると考える事が出来る事

となり、ミクロの現象を対象とする量子力学にプランク定数が常に現れる本質的

な意味が理解される。

　

ところで、拘束状態の電子からの光の放射時間Ｔは約１０^-8秒から約１０^-10秒

迄の広い幅があるとの情報を得た事により、光子のエネルギーはｈνで表現出来

ない事となると考えたが、式Ａに於いて一波長分の波のエネルギーｅが放射時間

Ｔと逆比例の関係にあれば成立する事となり、これまでの光子のエネルギーｈν

が実験値とも良く合っている事を考慮すれば、この状態が存在している事が示唆

される。

これが事実であれば、電磁気理論に於ける重ね合わせのない電磁波の一波長分の

エネルギーが周波数に関わらず一定という仮定を変更すべき事を意味している。

　

次に、光子のエネルギーを別の角度から検討する事とする。

光子の放射時間をＴ（一定値！），その間に観測される振動の回数をＮとすれば、

振動数ν＝Ｎ／Ｔの関係にあり、光子のエネルギーＥは、

　

Ｅ＝ｈν

　＝ｈ×（Ｎ／Ｔ）

　＝（ｈ／Ｔ）×Ｎ

　

となり、ｈ／Ｔは一定値（定数）であるので、光のエネルギーＥは、振動の回数

Ｎ（自然数）に比例し、ｈ／Ｔの離散値を持つ事となり、決して連続した実数値

をとる事は出来ない事が証明される。

因みに、ｈ／Ｔ（≒6.62×10^-28j）は、電磁波の１波長分のエネルギーｅである。

　

以上の考察から、光子のエネルギーがｈνという簡単な方程式で表現できる事か

ら、光子には放射時間という概念は必要無いという誤った理解がなされ勝ちであ

るが、電子からの光の放射時間は、光のエネルギーを決定する必須の因子であり、

現行の多くの理論で考慮されることが少ない事は大変不可解としか言い様がない。

　

ここで、量子論の出発点となったプランクの量子仮説、更にアインシュタインの

光量子仮説を再考する事とする。

黒体輻射の実験結果である輻射エネルギーと光の振動数のスペクトラムの関係図

を表現する方程式を確立する競争に於いて、レイリー＆ジィーンズやウイーンの

論理式がスペクトルの全域に渡り正しく表現できない状態であったが、プランク

は、ウイーンの式を少し手直しするだけでスペクトルの全域を正しく表現できる

新しいプランクの輻射公式を見い出し、更に、その式の中で光のエネルギーＥが、

　

Ｅ＝ｎｈν（ｎ；１、２、３、・・・）

　

というｈν単位で表現できるエネルギーの単位の存在が１９００年にプランクに

て導かれ、１９０５年になると、新しく発見された光電効果の実験結果を説明す

る為に、このＥ＝ｈνというエネルギーを担う一個の粒子（光量子）を仮定する

と、全ての光電効果の現象を上手く説明出来る事をアインシュタインが示して、

量子論の創設の切っ掛けを作った事は余りにも有名である。

光子のエネルギーの方程式；Ｅ＝ｈνから、下記の事柄が導かれる。

　

（１）任意の振動数の光の振動は全て同一の周期を持つ。

（２）任意の振動数の光の一周期分の振動に関するエネルギーは全て同一である。

　　　（１）と合わせると、任意の振動数の波の振幅が同一である。

（３）任意の振動数の光の電子からの放射時間（相互作用時間＝時間長）は一定

　　　でなければならない。

（４）上記（１）〜（３）から、任意の光の振動数は離散値しか取り得ず、光の

　　　エネルギーも離散値となる。

　

量子論の創生期のスタート時点に於いて、エネルギーは連続した物理量であり、

限りなく細分が可能という古来からのエネルギーの概念を無批判に継承した結果、

光の振動数が実数値を取り得る事により、振動数が連続した実数値を取り得ると

即断してエネルギーの連続性の概念を支持する実例となり、この考えが量子論の

中心的な概念となり、今日の場の量子論まで継承されて来ている事を銘記したい。

限りなく細分が可能な物理量という概念は、無限小という数学の抽象的な範疇の

概念であり、自然現象を対象とする物理学の具象的であるべき概念として無批判

に受け入れられている現状を、決して容認できるものでは無い。

尚、原子内に捕捉状態の電子から放射される黒体輻射や天体の発する自然光は、

アインシュタインの光量子仮説の式（Ｅ＝ｈν）に従う放射時間や振幅が揃った

光であるが、人工的な電波（ＴＶ波やラジオ波等）は、振幅や周期や放射時間を

自由に変化させる事が可能な光であり、この様に人工的に制御された自由電子か

らの放射光やプラズマ状態の自由電子からの放射光は、光のエネルギーを最早、

ｈνという単純な方程式で表する事が出来ない事を考えると、エネルギーをｈν

という方程式で表現出来る光子は、定常の状態の原子に捕捉された電子の放射光

であり、ドップラー効果が生じない光源と観測機器の相対速度がゼロという極め

て限定された状態の光にしか適用出来ない制限された光のモデルである事が解る。

但し、光の簡易のモデルとしての光子のこの様な欠点を弁えて使用すれば、光が

関わる大半の現象に於いて、光子のエネルギーを振動数のみで表現できる事によ

り論理展開が容易に論述できるメリットの恩恵は余りあると考える。

　

ところで、光のエネルギーが光を構成している波の個数（自然数）に比例すると

いう事が解った訳であるが、その他に、自然界に存在する物質に関しても、その

個数は当然ながら自然数という事になり、自然数以外の存在を想定する事は困難

と思われるので、自然に存在するエネルギーは離散的である事が推定される。

エネルギーを定量的に評価する際に現れる一見すると実数値で連続した数値とし

て導出されるエネルギー量は、単位時間で評価する際の数値の処理に際して生じ

る人為的な値であり、これを自然の本質であるエネルギーの連続性として誤った

評価を行っているのが現行の解釈と考える。

Ｃ節で論じるが、座標変換に於ける相対速度の変化に応じて物質の全エネルギー

（質量エネルギー＋運動エネルギー）が変化すると解釈している現行の力学理論

は間違いであると考えているので、物質の持つエネルギーは時間発展並びに座標

変換に於いても不変であり、エネルギーの不連続性（エネルギー素量）の考えが

保たれる事になり、この事柄に付随するエネルギーの連続性の考えは否定される

事になると考えている。

これはＥ節で論じる事とするが、ベクトル・ポテンシャルに関する現行の無限小

の運動量とエネルギーを持った電子の位相を変化させる実体という解釈は間違い

であり、幾らかの有限なエネルギーを仮定する事により、得体の知れない実体と

いう解釈では無く、一人前の物質（基本粒子）と解釈するべきと考えると、現行

の素粒子理論の基本から見直しが行われなければならない事になると考える。

　

B節＞素光子の基本性質

物理的に意味のある最小の基本単位として、プランク時間やプランク長が論理的

に導出されているが、エネルギーに関しては、エネルギー素量と呼ぶ基本単位が

設定されていない事からも、量子論では、エネルギーは限りなく細分可能である

という些か理解し難い基本的な考えが今なお堅持されている事が伺える。

この事が、量子の固有エネルギーの量子化という余分な過程を必要とし、素粒子

が質点（広がりの無い位置のみの情報を持った物質）という、これ又無限に小さ

い物質という数学上の抽象的な概念を受け継いできた古典物理学の概念を無批判

に継承している事が、発散の困難を生じる原因であり、量子論の発展に致命的な

ブレーキとなっている可能性を指摘したい。

このレポートの主旨も、結局は、この指摘事項の正否に掛かっている訳であり、

素光子というエネルギー素量を持った基本粒子の存在を仮定する事により、従来

よりも単純で明解な新しい統一的な自然観を描出しようとする本稿の種々の試み

により、その妥当性と既存の理論に対する優位性を主張しようとするものである。

　

物質が一点に集中する過程でブラック・ホールになる場合に、その事象の地平面

であるシュバルツシルト半径が物質の量子的な広がりであるコンプトン波長と等

しくなる場合に、その半径をプランク長と定義して、その質量をプランク質量と

定義されているが、エネルギーと質量の等価式にて換算されるプランク質量に対

するエネルギーをプランク・エネルギーと定義されている。

素光子を物理的に意味のある最小の長さとして定義付けられているプランク長の

直径の弾性率１の球体と仮定すると、物理的に意味のある最小の時間として定義

付けられているプランク時間は、（プランク長）／ｃとして定義されている事に

より、プランク時間とは素光子が他の物質と相互作用に要する時間に相当すると

いう事になるが、これは自然界に於ける最小の現象が生じる時間という合理的な

解釈が出来る事となる。

　

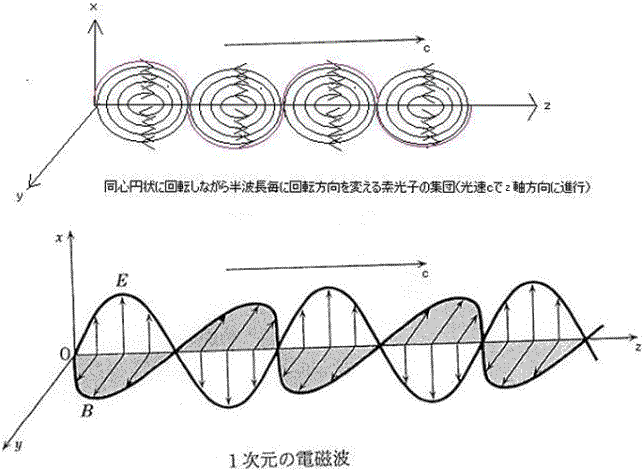
B節＞電磁波の素光子モデル

光子は、光と物質が振る舞う自然現象を理解する為に提示された光の粒子性に重

きを置いた１つのモデルであり、一方電磁波も光の波動性に重きを置いた１つの

モデルという観点から、光子の例に習って電磁波を素光子で置き換える事を試み

る事とする。

光が電子から放射される際の放射時間Ｔは、理論値（巻末の参考文献（Ａ））及

び実験値として、約１０^-8秒が確認されている。

そこで、エネルギーｈνを持った光子に相当する電磁波の１波長分のエネルギー

をｅとすると、放射時間Ｔの間に放射される電磁波の波の総数はνＴであるので、

　

ｅ×νＴ＝ｈν

∴ｅ＝ｈ／Ｔ≒１０^8×ｈ／ｓ＝１０^8×ε

　

つまり、エネルギーがｈνという形式で表現できる１個の光子に対応する電磁波

の１波長分の波は、素光子が約１０^8個集合したものとなる。

また、ベクトル・ポテンシャルが、電磁場の本質的な実体である事が実証されて

いる事を考えると、渦を巻くベクトル・ポテンシャルと電磁場の相互の関係から

類推すると、約１０^8個の素光子の集団が車輪の様に電磁波の運動方向に回転し

渦を巻きながら、光速で移動している描像（サイクロイドの軌跡）が推測される。

又、電場や磁場が半周期毎に振幅の方向が反転する事を考えると、素光子の回転

方向も半周期毎に逆転している事が推測されるが、光の進行方向から粒子の集団

を観れば、ベクトル・ポテンシャルの数学モデルである調和振動子の波動関数が

ガウス分布に従うという事から、素光子の渦の中心部が磁場の振幅方向にガウス

分布様に膨らんだソンブレロ銀河に似た形状を呈しているのではないかと予想す

る。（巻末の図２参照）

論理の大飛躍ではあるが、素光子の密度がガウス分布に従うことが、自然現象に

関する統計に於ける確率分布がガウス分布に従う事の本質的な原因かも知れない。

なお、素光子の回転面が電磁波の進行方向と一致する事を考慮すると、同心円状

に渦を巻きながら光速で運動している粒子の集団が運動方向を軸として進行方向

に対して右ねじの方向に回転する場合を現行の量子力学理論では＋のヘリシティ，

その逆を?のヘリシティと呼んでいる、所謂、円偏光の現象であるが、回転が無い

場合が直線偏光と呼ばれ、ヘリシティ０に相当する。

また、円偏光の電磁波と直線偏光の電磁波の混合状態は、偏光が合成されて楕円

偏光として観測される。

なお、電磁波を構成している１つの波自体が電磁波の運動方向を軸として実際に

回転運動を行っている訳では無く、前後の波の回転面の位相角度が規則的に変位

する為に、定点観測に於いて、波が回転している様に観測される事となるものと

推測すると、直線偏光とは位相角度が一定した波で構成されている事になる。

ところで、一般的な電磁波のイラストでは、巻末の図２の様に同じ位相の電場と

磁場の振幅の方向が直交して描かれているが、古いイラストでは位相が一波長分

ずれた状態で描かれている事が観られたが、これは動く電場が磁場を生じ、動く

磁場が電場を生じるという基本的な電磁気現象が電磁波を生じさせているという

誤った解釈に基づいていた事に依るが、実際の電磁波は電場としてのベクトル・

ポテンシャル（素光子）のみで構成されている事を考えると、磁場は動く電場の

二次的効果と考えると、現行の電磁波のイラストは正確な描写とは言えず、又、

電磁波という名称も的確とは言えなくなり、電磁波から磁場を取り除くと、多少

現行とは異なる概念であるが、電波という既存の名称に統一すべきかも知れない。

ところで、電磁波が電気的に中性である原因は、一波長分の波を構成する素光子

の集団の渦状の回転方向が半波長毎に逆方向を向いている為に、半波長分の電場

同士が打ち消し合って一波長分の電場がゼロとなる為であると推定する。

この結果、光という物質について、粒子性に重きを置いた光子のモデルと波動性

に重きを置いた電磁波のモデルを１つに統一する試みとしての素光子のモデルに

より、粒子性と波動性の両方を無理なく統一的に説明出来る事になると考える。

　

ところで、電磁波の波として素光子の集団がどの様な機序により集合するかとい

う問題があるが、電波の発生の際の電気双極子の振動によりトラスト様に集合し

た素光子の集団に於いて、トラスト状態から一波長分毎に分裂して放出される事

を振動の１周期毎に繰り返す事で、一連の連続した電磁波として放射される事に

なると考える。（参考文献（Ｄ)の（１４））

なお、空間を伝播中の素光子の集団が、渦状に回転しながら光速で運動している

というサイクロイド様の運動を行っているという描像は、素光子の渦状の運動は

光速を越える速度を持つことが必要となり、更に、慣性力としての遠心力を相殺

する為の向心力が必要という問題が生じる事となるが、光速での運動状態に於い

ては、速度の加法則により、（波の速度ｃ）＋（渦状の回転運動ｃ）⇒ｃとなり、

渦状の回転運動状態は静止した状態に観測される事となる結果、素光子の集団が

一塊となって光速で運動している描像が正しいのではないかと考えている。

　

B節＞素量子の基本性質

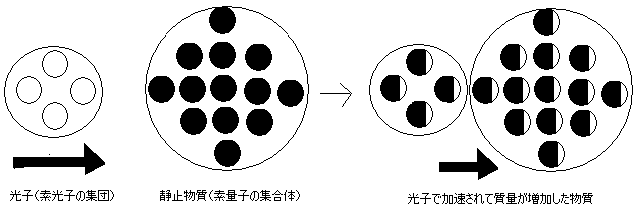
　核分裂や核融合に於ける質量欠損分の光の開放や、光からの正粒子と反粒子の

対生成や正粒子と反粒子の対消滅に伴う光の発生等の現象により、エネルギー

（つまり光）と質量（つまり、質量を有する物質）が相互に変換可能である事が

実証されている。

そこで、素光子説の核心となる基本概念である、「質量を有する物質は光が固ま

ったものではないか！？」という１９７３年以来の素朴で漠然的な着想を具体化

する事とする。

　

素光子同士が束縛状態になり、素光子の定常状態である光速での運動状態より遅

い速度でしか運動出来ない状態の素光子を素量子と呼ぶ事として、質量を有する

全ての物質の構成要素と仮定し、この基本的な性質を以下の様に想定する。

　

＜素量子の基本性質＞

　

　�T 素光子から素量子への移行（１個の素光子が素量子１個に対応）

　　 素量子は、光速で運動している質量がゼロの素光子同士が束縛状態になり、

　　 光速より遅い速度でしか運動出来ない事により質量を有し、下部構造を有し

　　 ない直径がプランク長程度の球状の下部構造有しない基本粒子と推定する。

　　 尚、素量子は素光子が元来持っている定常状態である光速ｃでの運動状態に

　　 戻ろうとする復元力を保持していると仮定すると、隣接する素量子間で一定

　　 の力で押し合い状態となり、合力０で力の均衡を保っている状態が想定され、

　　 素量子の集合体である全ての質量を有する物質を安定な状態に維持する機序

　　 を説明出来る可能性がある。

　　 更に、宇宙空間に量子力学で言う零点エネルギーに相当する自由素光子場が

　　 存在していると仮定すれば、周囲の素光子が光速ｃという一定の速度で均等

　　 に完全弾性衝突（お互いが弾性率１の完全剛体と仮定）する事で、素量子の

　　 集合体が自然崩壊する事を抑制する働きを担っている可能性がある。

　

　�U 素量子（素光子）のエネルギー不変の原理

　　 素量子は、最も安定した基本粒子であり、その全エネルギーが増加したり、

　　 減少したり、更には、他の粒子に変換されたり、分割されたりする事は無い。

　　 つまり、時間発展並びに座標変換に於いて、素量子の固有エネルギーは不変

　　 である。

　

　�V 素量子から素光子への移行

　　 素量子の集合体である全ての質量を有する物質に、素光子や他の粒子が作用

　　 して、素量子の間の力の均衡が破れると、束縛状態から解放されて素量子の

　　 単独の状態である素光子やその集団である光子や一連の粒子群に崩壊する。

　

　�W 素量子の基本物理量

　　 素光子の束縛状態というだけで、その他は素光子と全く同じ物理量を持ち、

　　 固有エネルギーεが、ε＝ｈ／ｓで、直径がプランク長であり、真の素粒子

　　 という位置付けから弾性係数１の完全剛体の性質を有する球体と推定する。

　　 固有質量ｍ０は、エネルギーと質量の等価式から、ｍ０＝ｈ／ｃ^2となるが、

　　 古典力学に準じる運動を行う古典的粒子と推定する。

　　 素光子の束縛状態の為に、任意の慣性系で光速より遅い速度しか取り得ない。

　

　

Ｃ節（素量子の運動状態の考察）

質量を有する全ての物質の構成要素としての素量子の運動状態について考察する。

　

C節＞ニュートン力学に基づくエネルギーと質量の等価式；Ｅ＝ｍｃ^2の導出

　核反応による物質の質量欠損や光子による反粒子の対生成、更には反粒子同士

の対消滅による光子の発生の事実を考えると、エネルギーと質量が等価である事

が示唆される。

　先ず、エネルギーと質量の等価式；Ｅ＝ｍｃ^2の本質に迫る為に、エネルギー

と質量が相互に変換できるという事を前提として、エネルギーと質量の変換係数

をニュートン力学の範疇で導出する論理展開を眺める事により、現行の力学理論

の要点及び問題点を洗い出し、素量子の運動状態式を想定する為の拠り所を掴み

たいと思う。

先ず、時間発展に於ける或る物質のエネルギーの変化を考察する為に、静止質量

m0の電子を加速器の電場のエネルギーで加速して、速度がｖに達した時の電子の

全エネルギーをEとし、付加したエネルギー量に応じて電子の質量が増加する様に

観測される事が実験により確かめられているので、その増加した質量をmとする。

そこで、質量mは加えるエネルギーの関数という事になるが、加えるエネルギーに

依り電子の速度が決定される事を考えると、質量mは速度の関数と考えられる。

また、結論から先に述べると、速度の関数としての質量の概念は、エネルギーを

与えられて物質が加速されて或る速度に達した場合に、その増加したエネルギー

分が質量に変換されたと見なされる場合にのみに該当し、座標変換に於いては、

エネルギーの授受など無い為に、相対論の言う相対速度に応じて質量が変化する

様な根拠は無いという事を改めて明記したい。

更に、結論から述べると、時間発展に於いて相対速度に依存して変化する質量は、

慣性質量とは異なる新しい概念の質量という位置付けが必要であると考えている。

座標変換に於いて質量は不変であると考えると、エネルギーと質量の変換係数は、

当然ながら相対速度に依存しないという前提が成り立つものとして、論理を展開

する事とする。

　

以下は、巻末の参考文献（Ｂ）を参考としながら、数式の展開を多少アレンジし

たものである。

　

エネルギーと質量が相互に変換可能である事が、多くの現象にて実証されている。

そこで、この事実を定式化する為にエネルギーEと質量mの変換係数をKと置いて、

Kの値を論理的に求める事とする。

ここで、質量mは速度つまり時間tの関数であり、変換係数Kは時間tの関数では無

いものと仮定する。

ところで、この仮定はニュートン力学の範疇を逸脱しているとの批判があり、こ

れに対しては、「物質は光が固まったもの」という素光子説の基本概念に立ち返

る事で、加速器による電子の加速運動に伴う電子の質量の増加という実証された

実験結果を拠り所として、時間発展に於いてのみ質量を時間の関数と見なす事が

出来ると判断し、ニュートン力学の概念のみを使用し相対論の概念は使用しない

という基本方針を保持しながら、以下の論理展開を行う事とする。

　

そこで、エネルギーEと質量mの関係式は、変換係数Kを介して、

　

E=m･K　･････(1)

　

の関係にあるものとする。

　

加速器の電場にて電子を加速するという設定の基に、論理の展開を行う。

先ず、電子が加速器に静止している時の質量（静止質量）をm0とすると、

その質量エネルギーE0は、式（１）の関係を参考にして、

　

E0=m0･K

　

と置ける。

　

ここで、質量m0の電子にエネルギーEを与えて力Fを働かせて、運動エネルギーを

与える事とする。

速度vで時間tの間に移動した距離をLとすれば、

　

L=vt

　

ところで、力Fと距離Lの積FLは仕事の単位（エネルギーΔE）であるが、実際は、

力Fを与えると加速度が生じて速度vは一定では無くなる為に、FLとFvtは近似的に

等しい事になる。（この節の考察は速度を線形の物理量として論述しているが、

Ｄ節で述べる速度の概念を線形から非線形に変更した場合の考察も必要である）

　

ΔE=FL≒Fvt

　

∴dE/dt=F･v　･････(2)

　

又、力Fは運動量p(m･v)の時間tでの微分であり、質量mは速度vの関数と考えると、

　

F=dp/dt=d(m･v)/dt

　

この式と式(1)の関係から、式(2)は、

　

d(m･K)/dt=v･d(m･v)/dt

　

この左辺のKは時間の関数では無いという仮定から、時間微分での定数として微分

が及ぶ括弧の外に出すことが可能となり、

　

K･dm/dt=v･d(m･v)/dt

　

算術的な技法を使う準備段階として、両辺に2mを掛けると、

　

K(2m)dm/dt=(2m･v)d(m･v)/dt　･････(3)

　

次に、算術的な技法を使用して、両辺を積分した形にして微分係数を無くす操作

を行う。

式(3)の左辺の(2m)dm/dtは、m^2を時間tで微分したものであり、

式(3)の右辺の(2m･v)d(m･v)/dtは、(m･v)^2を時間tで微分したものである。

よって、式(3)は、

　

K･d(m^2)/dt=d((m･v)^2)/dt　･････(4)

　

と同じである。

この方程式の両辺の微分係数が等しいならば、その両辺の式自体には或る定数の

差があるだけであるから、その定数をAと置けば、式(4)は、

　

K･m^2=(m･v)^2+A　･････(5)

　

と置ける。

これに、物質の速度vが0の時の質量mがm0を代入すると、

　

K･m0^2=0+A

∴A=K･m0^2

　

これを式(5)に代入すると、

　

K･m^2=(m･v)^2+K･m0^2

∴m^2(K-v^2)=K･m0^2　　･････(6)

　

ここで、Kは速度の２乗の次元でなければならない事が分かる。

更に、Kが正の実数であるので、式(6)の左辺が物理学的に意味を持つ為には、

　

K-v^2>0

　

が必要であり、

　

v<√K

　

となるが、この不等式の意味する事は、物質の速度ｖが或る有限の速度√Kを上限

とするという事であり、従って、√Kは実験で実測されている最高の速度である光

の速度c（普遍定数）という事になり、

　

√K=c

∴K=c^2

　

これを式(1)に代入すると、

　

E=m･c^2　･････(7)

　

という、目的のエネルギーEと質量mの等価式が導かれる。

　

更に、これを式(6)に代入すると、

　

m^2(c^2-v^2)=m0^2･c^2

∴m･c^2=m0･c^2/√(1-(v/c)^2)　･････(8)

　

式(7)の意味を考慮すると、式(8)の左辺は物質の全エネルギーEを意味し、

　

E=m･c^2=m0･c^2/√(1-(v/c)^2)　･････(9)

　

この方程式は静止状態の電子（静止質量m0）にエネルギーを与え、速度ｖに達し

た時の電子の全エネルギーEを表す方程式である事が分かる。

ここで、式(8)の両辺をc^2で割ると、

　

m=m0/√(1-(v/c)^2)　　･････(10)

　

よって、良く知られた相対論的質量に関する方程式と同じ式を導出した事となる。

この結果は、質量mが速度つまり時間の関数であり、変換係数Kが定数つまり時間

の関数では無い事となり、以上の論理展開の前提である仮定を満足する事となる。

　

　以上のエネルギーと質量の変換係数の導出過程は、ニュートン力学の範疇で、

静止した物質に、外部からエネルギーを与えて、或る速度ｖに達した時の物質の

質量が与えたエネルギーに連れて質量が増加する、つまり、質量が物質を加速す

る為に与えられたエネルギーにより達成される速度の関数である事を仮定すると、

全エネルギーを導出する過程で、変換係数Kが論理的に決定されたものである。

ここで興味深い事柄は、ニュートン力学の範疇でローレンツ因子と同じ式が導出

され、しかも相対論的質量に一致する式(10)が導出された事である。

尚、核反応時のエネルギー発生に対応した質量欠損や光同士の衝突による反粒子

同士の対生成や反粒子同士の衝突による光の発生等で実証されているエネルギー

と質量の等価性に加えて、今回の物質を加速させる為に加えられたエネルギーが

物質の質量増加に関与する事実は、物質がエネルギーを担う基本粒子（素光子）

から構成されている事を強く示唆する現象と考えられる。

ここで、この様な特殊相対性理論に特有と考えられ勝ちな式が導出される背景を

考えると、エネルギーと質量の等価性を前提としてニュートン力学とエネルギー

保存則、更に、物質の最高速度ｃを使用しただけで導き出されたという事である。

つまり、相対論の前提の要の光速不変の原理を利用する事無く、相対論的質量に

一致する式(8)が導出された事の意味を、少し考えてみたい。

光の最も重要な性質である光速不変の原理は、時間発展に於いては不必要であり、

光速不変の原理を前提とする特殊相対性理論と同様な式が導出された根本の原因

は、質量を有する物質は或る速度（つまり光速ｃ）より遅い速度でしか運動出来

ないという最も重要で基本的な物質の性質が論理的に導かれたという事である。

尤も、光速不変の原理は、慣性系の座標変換の公式であるローレンツ変換に於い

て必要となる前提である事を考えると、座標変換に於いてのみ必要であり、時間

発展に於いては必要としない事は当然と言える。

更に、物質にエネルギーを与えて加速しようとしても、極限の速度（光速ｃ）に

近づくに連れて速度の加算が頭打ち状態になるという事を意味するものであり、

この現象は相対論の時間の遅れと定量的に一致するものと推測する。

つまり、この現象も、光速不変の原理を前提とする特殊相対性理論とは独立に導

かれた事を強調したい。

つまり、光速不変の原理の産物と考えられ勝ちなローレンツ因子が、光速不変性

とは無関係に導出出来た事は、最も基本的な何らかの自然の摂理の存在を示唆し

ているのかも知れない。

この事柄も、物質が光速ｃで常に運動している素光子の束縛状態である素量子が

全ての質量を有する物質の構成要素と考えれば、至極当然の事と思われる。

所で、座標変換に於いては、相対速度に応じて運動エネルギーの変化分が物質の

全エネルギーを変化させると考えるニュートン力学とそれを踏襲する相対性理論

は、エネルギー保存則を満足しないという重大な問題を抱えている事となる。

つまり、時間発展に於いては、エネルギー保存則を中心にして論理展開を行い、

特殊相対性理論の結果と同等な式（ローレンツ因子）を導出出来た訳であるが、

座標変換に於いては、エネルギー保存則を満足しないとなると、果たして論理的

に一貫した正しい結果を得ていると言えるのであろうか！？

尚、エネルギーと質量の等価式；Ｅ＝ｍｃ^2は、時間発展のみならず、座標変換

に於いても成立する普遍的な等価式と考える。

物質にエネルギーを与えて加速すると、相対論的な質量増加と同じ式が導かれた

が、これは、与えたエネルギーが物質（つまり質量）に変換されると仮定すれば、

エネルギーと質量の等価式が導出されるという或る意味当然の事であり、決して、

座標変換に於ける相対論的質量増加を証明したものでは無いという事である。

　

自由電子をサイクロトロンの電場で加速して或る速度に達した場合に、加速に要

したエネルギー分の質量が増加する事になるが、実際に、このエネルギーがどの

様な状態で自由電子に付加されているのかを考えると、現行の理論では光の衣を

纏っているという表現がなされ、リングで運動中の自由電子に掛かる強い遠心力

が光の衣の結合力（引力？）を越えると、光の制動放射が生じる事となる。

一方、原子核に捕捉されて束縛状態にある電子の場合は、電場では無く光自体が

電子に吸収されて励起状態となり、上位の軌道に遷移する事となるが、不安定な

場合には速やかに直前に吸収した光を放出し、元居た低位の軌道に戻る事となる。

この２つの例では、加速するエネルギーの形態は異なるが、何れも光という形態

のエネルギーを放出する事に注目しなければならない。

問題は、電場（素光子の集団）がどの様な状態で自由電子に付加しているかとい

う事であるが、今後の課題としたい。

　

C節＞素量子の運動状態式の導出

此までの予備知識を踏まえて、質量を有する全ての物質の構成要素である素量子

の運動状態に於ける質量エネルギーと運動エネルギーについて検討する事とする。

加速器の電場のエネルギー（即ち、素光子の集団）で電子を加速する場合を想定

して、時間発展に於ける素量子の運動状態の推移を論理展開する。

　静止状態の物質Ｓ（素量子の集合体で、質量Ｍ0＝ｎ0*ｍ0、ｎ0はＳを構成して

いる素量子の個数、ｍ0はその静止質量）に、エネルギーＥ1（Ｅ1＝ｎ1*ｅ;εは、

素光子の固有エネルギーで,ε＝ｍ0*c^2、ｎ1はｎ0と同様にエネルギーとしての

光の構成要素である素光子の個数、ｃは光速）を加えて加速して、物質Ｓがある

速度に達した状態を考える。

　

物質Ｓの全エネルギーをＥとすると、

　

Ｅ＝ｎ0*ｍ0*c^２　　（静止質量エネルギー）

　　＋Ｅ1　　　　　　(加えたエネルギー）

　＝ｎ0*ε　　　　　　･･･ Ａ項

　　＋ｎ1*ε　　　　　･･･ Ｂ項

　＝(ｎ0＋ｎ1)*ε

　

∴Ｅ＝(ｎ0＋ｎ1)*ε

　

　ここで、素量子の質量エネルギーと運動エネルギーの関係について考察する。

Ｂ節の�Uにより素量子の全エネルギーが不変であるという条件を課すと、静止時

には、全エネルギーは質量エネルギーのみであるが、運動速度が増加するに連れ

て、運動エネルギーが増加し、その分だけ質量エネルギーが相補的に減少する事

が必要となり、速度が光速ｃに限り無く近づくに連れて、質量エネルギーが限り

なく０に近づき、極限の光速ｃの状態（素光子の状態）では質量エネルギーが０

となる結果、論理的に質量が０（光の質量がゼロ）となる事が導かれる。

　

これらの事柄を踏まえ、巻末の図１の素量子の集合体がエネルギーを与えられて

加速される結果、或る速度の運動状態に達した場合の概念図を念頭に置きながら、

この式の右辺を質量エネルギーと運動エネルギーとに論理上都合が良い様に分離

する事を試みる。

無次元の変数α（０＜＝α＜＝１）を用いて、恒等式の形式をとりながら、質量

エネルギーの項と運動エネルギーの項に分離させると、

　

Ｅ＝(ｎ0＋ｎ1)*ε

　＝α*(ｎ0＋ｎ1)*ε　　　　 ･･･ Ｃ項（質量エネルギーの項）

　＋(１−α)*(ｎ0＋ｎ1)*ε　 ･･･ Ｄ項（運動エネルギーの項）

　

尚、αは、静止状態では１、光速ｃの場合は０となる速度に関連すると思われる

無次元の変数である。

ここで、時間発展に於ける（運動）エネルギー保存則にて、Ｂ項とＤ項が等しい

と置くと、

　

ｎ1*ε＝(１−α)*(ｎ0＋ｎ1)*ε

∴α＝ｎ0／(ｎ0＋ｎ1)

　

この式で、ｎ１（加えるエネルギーである素光子の個数）が増加すると、物質Ｓ

の速度が増加する事となるが、加えるエネルギー量（ｎ1の個数）を線形に増加さ

せるのに対応し、αは非線形に減少する事が判る。

このαとｎ1は、原点を（0,-ｎ1）とする反比例のグラフの関係にあり、この座標

を９０度回転すれば、一般的な双曲線となる。

次に、加速の結果生じる実際に観測される速度ｖとαの変化を関係付ける方程式

を求める事とする。

ここで、この節の冒頭でのエネルギーと質量の等価式を論理的に求めた結果を踏

まえて、静止質量Ｍ0の電子を加速器で加速した結果、速度がｖに達した時の電子

の全エネルギーＥの理論値の正しさが実験により実証されている事を用いると、

式(10)から、

　

Ｅ＝(ｎ0＋ｎ1)*ε＝ｎ0*ｍ0*c^2／√(１−(ｖ／ｃ)^2)　･･･ Ａ式

　

と置けるが、この右辺の式は、静止質量Ｍ0（＝ｍ0*ｎ0）の物質Ｓにエネルギー

ｎ1*εを加えて、速度がｖとなった時の物質Ｓの全エネルギーを表す式である。

そこで、ε＝ｍ0*c^2を考慮して、Ａ式を変形すると、

　

ｎ0／(ｎ0＋ｎ1)＝√(１−(ｖ／ｃ)^2)

　

となり、この式の左辺はαそのものであるので、

　

α＝√(１−(ｖ／ｃ)^2)

　

となり、目的の素量子の質量エネルギーの減少率αと速度ｖの関係式を得る事が

出来た事になる。

この式から、速度ｖが線形に増加するに従い、αは確かに非線形に減少する事が

解る。

このαとｖの関係は、楕円（ｃ^2*α^2＋ｖ^2＝ｃ^2）の第１象限での性質を持つ。

前に求めたαとｎ1（与えたエネルギーに於ける素光子の個数）の関係が反比例や

双曲線の性質である事と対比させる事も、今後の論理の展開上必要であろう。

また、αは、元来、素量子の速度ｖに関する質量エネルギーの減少率であるが、

特殊相対性理論のローレンツ収縮率と一致する事も注目すべき事柄である。

勿論、質量の減少が物質の収縮の現象として観測されるとは予想してはいない。

よって、静止した物質Ｓにエネルギーを加えて加速して速度ｖに達した物質Ｓは、

素量子が（ｎ0＋ｎ1）個集合した物であり、固有エネルギーεが（ｎ0＋ｎ1）倍

となり、全エネルギーＥとなっている事を考慮すると、質量を有する全ての物質

の構成要素である素量子の速度ｖに於ける質量エネルギー及び運動エネルギーの

速度ｖに於ける運動状態式は、下記の如くになる。

　

ε＝(√(１−(ｖ／ｃ)^2))*ｍ0*c^2　（素量子の質量エネルギーの項）

　 ＋(１−√(１−(ｖ／ｃ)^2))*ε　（素量子の運動エネルギーの項）

　

この式の右辺の第一項において、素量子の質量ｍ＝(√(１−(ｖ／ｃ)^2))*ｍ0と

考えると、ｍは確かに速度ｖの関数である事が分かる。

ここで、この素量子の運動エネルギーと古典力学に於ける運動エネルギーの関係

について調べてみる。

　

（素量子の運動エネルギーの項）

＝(１−√(１−(ｖ／ｃ)^2))*ε

＝ε*(１-√(１-(ｖ/ｃ)^2))*(１+√(１-(ｖ/ｃ)^2))/(１+√(１-(ｖ/ｃ)^2))

＝ｍ0*ｖ^2／(１＋√(１−(ｖ／ｃ)^2))

　

ここで、（素量子の速度ｖ）≪（光速ｃ）の場合は、（上式の分母） ⇒ ２

　

∴（素量子の運動エネルギーの項） ⇒ ｍ0*ｖ^2／２

　

となり、古典力学の範疇（ｖ≪ｃ）での運動エネルギーに一致する事が分かる。

　

上記の恒等式は、時間発展に於ける素量子の運動状態式であるが、素量子の固有

エネルギーε（ｈ／ｓ）が座標変換に際しても普遍という条件を課すと、慣性系

に於ける座標変換に際しても成立する事が推測され、素量子の集合体である質量

を有する全ての物質が座標変換に際してもエネルギー保存則が成立する事となる。

つまり、慣性系の座標変換を考察する際の基本方程式となり得る事を意味するが、

座標変換に於いてもこの恒等式が成立するとする仮定が、ガリレイ以来の相対性

原理と同じ意味合いを持つ事になり、現行の些か曖昧な表現で定義付けられてい

る相対性原理に代わり、素光子説に於ける新しい単純で明確な相対性原理と位置

付けては如何であろうか！？

なお、この原理が普遍的に成立するかどうかは、今後、厳密なる論理的な検討及

び検証が必要である。

この原理は、ニュートン力学や特殊相対性理論に於ける慣性系の座標変換に際し

てはエネルギー保存則が成立出来ない事に対する最大の優位性の現れと考える。

逆に考えると、任意の慣性系の物理現象が同等に生じる事を主張する相対性原理

はエネルギー保存則を要請していると解釈すべきであろう。

更に、質量の無い光子の場合は座標変換に際し光子の振動数νがドップラー効果

に依り変動する事から、光子のエネルギー（ｈν）は、座標変換に於いて保存し

ないと短絡的に考えられているが、光子も電磁波と同様に他の物質との相互作用

時間が存在する事を考慮すると、光子の振動数と相互作用時間は逆比例の関係に

ある為に、観測される光子のエネルギーに変化は無く、座標変換に於ける光子の

エネルギーも保存されているものと考える。

以上の様に、光も含めて全ての物質について、時間発展並びに座標変換に於いて、

エネルギー保存則が成立するものと考える。

以上の考察から、相対性原理とは、時間発展並びに座標変換で、素量子の状態式

が一様に適用できる事を要請しているものと考える事が出来る。

　この素量子の運動状態式の質量（質量エネルギー）の項を観ると、速度を線形

に増加させると、質量（エネルギー）が非線形に減少する事が解るが、これは、

相対論的質量（座標変換にてエネルギー保存則が不可）とは正反対の変化である。

この質量の変化により、質量を有する物質の運動の極限ｃに於いて、質量がゼロ

となり、素光子の集団である光子の質量がゼロである事が、自然に導かれる。

　

　質量の定義は、「物質の動き難さの指標」であるが、運動エネルギーを同様に

考えて、「物質の運動状態の指標」と見なすと、質量とエネルギーは、表裏一体

の同一の存在の相補関係にある一方の側面を観ているものと言えよう。

又、運動エネルギーを顕性のエネルギーに例えると、質量がゼロの素光子が束縛

状態になると、光速より低下した速度に応じて素量子が質量を獲得し、素量子の

運動エネルギーが減少した分が質量エネルギーとなり、これを不顕性エネルギー

に例える事が出来る。

座標変換に依る相対速度に応じて、物質の運動エネルギーが変化する事は、何か

不思議な感じがするが、素量子の顕性エネルギーと不顕性エネルギーが相対速度

に応じて相補的に変化すると解釈すると、違和感も無くなるであろう。

例えば、裸の電子（静止質量Ｍ0）にエネルギー（電磁場）を加えて速度ｖに達し

た場合は、現行の考えでは、電磁場（加えられたエネルギー）の衣を着た電子と

なるという曖昧な表現が使われているが、素光子説では、与えられたエネルギー

である素光子の集団が半束縛状態となり、電子の周囲を光速ｃで旋回している事

で質量増加に関与しているという解釈が可能となり、この節のＡ式の様に丁度、

相対論的質量と同等の式である質量Ｍ＝Ｍ0／√(１−(ｖ／ｃ)^2)の関係で質量が

増加している事となる。

また、この質量増加が相対論的質量と同じ式となったのは、偶然の結果では無く、

ニュートン力学の範疇で求められた前記のエネルギーと質量との等価式の導出の

際の時間発展に於ける質量増加の割合が自然現象の基本的な性質の現れであると

解釈する事で納得する事が出来る。

もし、座標変換（エネルギーの関与が無い）に於いても相対論的質量増加が生じ

るとすると、電子を加速する際の質量増加に於いて、エネルギーの関与による真

の質量増加に加えて速度の増加に伴う相対論的質量増加が加わる事となり、実際

の観測値の２倍の質量増加が生じなければならない事となり、これは実験事実に

反する事である。

つまり、時間発展に於いては、相対論的質量増加と同等の質量増加は生じるが、

座標変換に於いては、物質を構成する素量子の質量エネルギーと運動エネルギー

の割合が相対速度に依存して相補的に変化するのみで、常に不変であり、現行の

力学理論の様に、相対速度に応じて運動エネルギーの増加が物質の全エネルギー

の増加をもたらすとする解釈は間違いであると考える。

これは、エネルギー保存則の普遍性を尊重する立場からも当然の事柄と言えよう。

最近では、相対論的質量は多くの不都合を生じるとして、誤った概念という考え

が共通した認識となっており、質量とは静止質量（速度の関数では無い）を指す

という事になっているが、この節の冒頭でのＥ＝ｍｃ^2を求める過程で、質量を

速度の関数と仮定した事と矛盾する結果をもたらす事となる。

　

以上の結果、素量子の運動状態式に現れる質量ｍ(＝ｍ0√(１−(ｖ／ｃ)^2)）は、

元来の質量という概念（慣性質量や重力質量）とは馴染めない事が分かる。

そこで、質量の概念を拡張し、運動中の物質の運動エネルギーを顕性エネルギー

と考えて、それと相補的に変化する不顕性エネルギー（素光子同士が束縛状態と

なり素光子の運動エネルギーとして発現していない閉じこめられたエネルギー）

の割合を表す指標としての質量という概念を新たに定義する事を提案する次第で

ある。

この結果、光速以下でしか運動できない質量を有する物質と光速で運動する質量

を有しない光とを新しい質量の概念の基で統一的に説明する事が可能となるもの

と考える。

　

現行の理論では、Ｅ＝ｍｃ^2として表されるエネルギーと質量の等価性の式に於

いて、ｍは静止質量を指し、運動中の物質の質量（即ち相対論的質量）を指すこ

とは不適当であるとの解釈に合意が出来てきているが、それでは、物質が光速に

近づくに連れて加速し難くなる現象を説明する手段を失う事となる。

尚、オリジナルのローレンツ変換を構築したローレンツが、１８９９年に相対論

的質量と同等の質量増加の概念を導き出しているが、ローレンツ変換を修正して

特殊相対性理論を構築したアインシュタインは、当初から相対論的質量の概念に

ついては否定的な見解を持っていたという歴史的経緯がある。

　

この節での考察の結果を簡単に纏めると、質量を持った全ての物質を、定常状態

が光速で運動している素光子同士が束縛状態となり、最早、光速では運動出来な

い状態の素光子（＝素量子）の集合体と仮定すれば、素量子の固有エネルギーが

不変という条件を課せば、物質にエネルギーを与えて加速した結果、或る速度に

達した物質の運動エネルギーが非線形性に増加する事が予想され、エネルギーと

質量の等価式を論理的に求める過程で得られた質量増加の方程式及び加速器によ

る電子の加速実験で得られた結果が予想値と一致した事により、素量子の速度を

パラメータとする質量エネルギーと運動エネルギーの関係を表す状態式を導出す

る事が出来た。

なお、振り返って、加速器にて電子にエネルギーを与えて加速する実験は、或る

意味、質量を有する全ての物質を素光子の束縛状態である素量子の集団と仮定し

た場合に、素量子の集団の振る舞いを考察し、更に、この仮定の妥当性を実証す

る最も理想的な実験であるとも考えられる。

最後に、エネルギーと質量の等価式をニュートン力学の範疇で求める過程で質量

を速度の関数と見なすことが必要であったが、これは、エネルギーと質量を等価

と見なす為の便宜上の電子を加速器で加速する様な時間発展に限り許される応急

の処置であり、座標変換（エネルギーの授受無し）に於ける相対論の解釈は誤り

であると考える。

別の見方をすれば、加速器での加速された電子の振る舞いは、電子が下部構造を

有しない素粒子では無く、下部構造（構成要素が素粒子）を有している事を暗に

示唆していると考える事が出来る。

　

Ｄ節（非線形速度の概念の提案）

　次に、この素量子の運動状態式を用いて、素量子の運動エネルギーが非線形性

に増減する事が、物質の振る舞いとして具体的にどの様に現れるかを検討する事

とする。

　

D節＞非線形速度の性質を表す方程式の導出

　Ｃ節の素量子の運動状態式の中で、運動エネルギーの項に着目して、物質Ｓ

（ｎ0個の素量子の集合体）をエネルギーＥ1（ｎ1個の素光子の集団）で加速した

場合に達する速度を静止時と運動時に分けて比較し、その変化の割合を検討する。

　

素量子の運動状態式(ε;素量子の固有エネルギー,ε=m0*c^2,ｖは慣性系の速度)

ε＝(√(１−(ｖ／ｃ)^2))*ｍ0*c^2　（素量子の質量エネルギーの項）

　 ＋(１−√(１−(ｖ／ｃ)^2))*ε　（素量子の運動エネルギーの項）

　

（１）静止時

与えたエネルギーＥ１（ｎ１個の素光子の集団）が全て物質Ｓの運動エネルギー

に変換されて速度ｖ1になったとすると、エネルギー保存則により、

（与えたエネルギーＥ１）＝（物質Ｓの運動エネルギー）であるので、

　

ｎ1*ε＝（１−√(１−(ｖ1／ｃ)^2))*(ｎ0＋ｎ1)*ε

∴ｎ1／(ｎ0＋ｎ1)＝１−√(１−(ｖ1／ｃ)^2)　･･･ Ｂ式

　

（２）運動時

先ず、Ｃ節での考察の結論から、座標変換に於いては、物質の相対論的質量増加

は生じない事を前提とする。

つまり、当然ながら、座標変換に於いて、物質Ｓを構成している素量子の個数は

不変であるという事になる。

速度ｖで慣性運動している物質Ｓ（ｎ0個の素量子の集合体）に、その運動方向に

エネルギーＥ1（ｎ1個の素光子の集団）を与えた場合に、物質Ｓの速度がｖ2に達

したとすると、エネルギー保存則により、

　

(１−√(１−(ｖ/ｃ)^2))*ｎ0*ε ･･･ 速度ｖで運動中の物質Ｓの運動エネルギー

　　　　　　　　 　　 ＋ｎ1*ε ･･･ 物質Ｓの加速に用いたエネルギーＥ1

＝(１−√(１−(ｖ2/ｃ)^2))*(ｎ0＋ｎ1)*ε ･･･ Ｅ1で加速した結果、速度ｖ2に

　　　　　　　　　　　　　　　　　　　　　　 達した物質Ｓの運動エネルギー

　

∴ｎ0／(ｎ0＋ｎ1)＝√(１−(ｖ2／ｃ)^2)／√(１−(ｖ／ｃ)^2) ･･･ Ｃ式

　

Ｂ式とＣ式の左辺同士を加えると１となる事に注目して、両辺を足し合わせると、

　

１＝１−√(１−(ｖ1／ｃ)^2)＋√(１−(ｖ2／ｃ)^2)／√(１-(ｖ／ｃ)^2)

√(１−(ｖ2／ｃ)^2)／√(１−(ｖ1／ｃ)^2)＝√(１−(ｖ／ｃ)^2)

　

ここで、両辺を２乗して整理すると、

　

√(ｖ2^2−ｖ^2)＝ｖ1*√(１−(ｖ／ｃ)^2)

　

が導かれる。

　

この左辺は速度ｖで慣性運動時に物質ＳにエネルギーＥ１が加えられて加速され、

増加した分の速度を表し、右辺は物質Ｓが静止時にエネルギーＥ1が与えられ加速

されて達した速度ｖ1が、物質Ｓが速度ｖの慣性運動中に同じ量のエネルギーＥ1

が与えられた場合に、相対論の時間の遅れと同等の運動の鈍化を来している事を

表している。

この現象は、物質の運動速度が光速ｃに近づくに連れて運動方向への物質の加速

効果が低下する傾向が増加するために、「物質の運動の頭打ち現象」と呼ぶ事と

する。

「物質の運動の頭打ち現象」を現行の力学理論に取り込む事を考えると、現行の

速度の線形の概念を非線形の概念に変更する事と等価ではないかと考える。

　

ここで、非線形の速度の概念の妥当性について、少し検討してみる。

ガリレイ変換は、速度の線形性及び無限大まで許容されるという古来からの自明

と考えられてきた概念をそのまま継承されて作成された慣性系の座標変換であり、

速度の加法則は、

　

ｖ＝ｖ1＋ｖ2

　

という、当然ながら四則演算が可能な形式である。

　

一方、ローレンツ変換は、光速不変性及び速度の最大値が光速ｃという１９世紀

末の大発見を前提としてアインシュタインにより構築された座標変換式であるが、

速度の線形性をガリレイ変換と同様に無批判に継承している事に留意すべきであ

る。

この速度の加法則は、

　

ｖ＝(ｖ1＋ｖ2)/(1+ｖ1･ｖ2/ｃ^2)

　

となり、最早、四則演算が出来ない、所謂、非線形速度の性質を暗に表したもの

と解釈される。

また、これ迄の全ての観測結果により、非線形速度の必要性が実証されている。

つまり、ローレンツ変換は、速度の最大値が光速ｃという概念を取り入れた時点

で、物体の運動に於いて、最高速度ｃに近づくに連れて速度の加算が頭打ちにな

る現象が想定される事となり、速度に関する線形の概念を非線形に変更すべきで

ある事を示唆しているものと考える。

　

線形の変数をｖとすれば、ｖは四則演算及び微積分が可能な変数という事が定ま

るが、現行の数学理論では非線形の数の概念が無いので、明示的に擬似の非線形

の数としてｕを使用する事とすれば、非線形の変数ｕの場合は四則演算や微積分

が出来ず、更に非線形の性質を持った数は無数に定義可能である為に、この変数

の性質を表す為には、何らかの線形のパラメータを使用した関数を介して間接的

に非線形数の性質を表現することが必要となるが、非線形に変化する変数ｕが果

たして線形のパラメータの組み合わせで表現出来るかどうかは、実際に試してみ

ない事には判定できないであろう。

慣性系の一次変換であるローレンツ変換は、線形代数の連立一次方程式の解を求

める方法で変換式が決定されるが、非線形速度を導入した新しい座標変換方式を

求める場合には、先ず、第一の関門として、線形代数の範疇でのローレンツ変換

に準じた既存の方法（連立一次方程式の解法）で座標変換の方程式を定式化する

事が不可能である為に、新しい何らかの方法を模索する事が必要となる事に注意

しなければならない。

　

ここで、これまでに意外と深く考察された事が無いと思われる速度差と合成速度

という２つの概念の本質的な違いについて考えてみる。

或る速度ｖで慣性運動中の座標系に於ける光は、光速不変の原理にて常に光速ｃ

で観測される。

すると、慣性系の運動方向と順方向に向かう光の場合は、慣性系の速度ｖと光の

速度ｃの差（速度差）は（ｃーｖ）となり、慣性系の運動方向と逆方向に向かう

光の場合の速度差は、（ｃ＋ｖ）となる。

速度差は、0から2ｃ（光同士が逆方向に向かう場合）の値を取る速度の単位とし

て慣用的に使用されている様であるが、明確な定義があるのかどうかも定かでは

無い。

ここで、最も重要な事柄としては、速度差として計算できる２つの物体の速度は、

何れの速度も観測者が直接観測できる速度に限られるという事である。

この例では、慣性系の速度ｖは直接観測される速度であり、光速ｃも直接観測さ

れる速度という事で、慣性系に於ける光の運動状態を速度差という速度の単位を

持つ物理量を利用して定量的に計算して評価できる事となる。

この様に考えると、光の振る舞いを考察する場合は、任意の慣性系で光の速度は

常に光速ｃで観測される事により、慣性系の運動と光の運動の差は常に速度差と

いう物理量で定量的に評価される事となり、光とは、質量を有して光速より遅い

速度でしか運動できない物体とは異なる特異な性質を有する物質であるという事

が改めて実感される。

速度差に関する更に重要な事柄は、速度差の２つの要素は何れも非線形速度では

あるが、非線形速度と特に意識する必要も無く、線形速度と同様な加減算が可能

という事になる。

　

次に、速度の合成について考える。

合成速度は直接観測される速度であり、速度差として直接計算可能な速度である

事を再確認すると、元来、合成速度を求める目的も速度差を求める一つの過程で

ある事も再認識されるべきである。

或る慣性系に静止した観測者が速度ｖ0（非線形速度ではｕ0）で運動中の物体を

観測するものとして、この慣性系が観測者に対しｖの相対速度で運動中の場合を

考える。

　

速度が線形で無限大まで許容されるガリレイ変換では、この慣性系の運動物体の

速度ｖ1は、速度の加法則により、

　

ｖ1＝ｖ＋ｖ0

　

となり、文字通り四則演算が可能な無限大まで許容される線形速度の性質で表現

されており、速度差を表す方程式（ｖ又はｖ0の符号が逆）と同じ形式となる。

　

速度の上限が光速ｃ（及び光速が一定値ｃとして観測される）である事が発見さ

れて、この速度の性質を前提として構築された座標変換がローレンツ変換であり、

この速度の加法則は、

　

ｖ1＝（ｖ＋ｖ0）／（１＋ｖ*ｖ0／ｃ^2）

　

という形式で表現されて、右辺の分子はガリレイ変換の速度の加法則そのもので

あり、部分的に線形速度の加算の性質及び速度差を表す方程式と同じ形式を留め

てはいるが、右辺の分母の効果にて、全体としては合成速度ｖ1が光速ｃを越えな

い様に構成されている。

　

一方、非線形速度の概念の基では、最早、ｕ１＝（ｕ＋ｕ0）*ｋの様な形式とし

て、ガリレイ変換の場合は、ｋ＝１、更に、ローレンツ変換の場合は、ｋ＝１／

（１＋ｖ*ｖ0／ｃ^2）)のような線形速度の加算の形式の表現は許されず、非線形

速度ｕを因子とする関数としてのｋ(ｕ)を、非線形速度の加算の場合の非線形の

性質を表す接続係数（仮称）として、

　

ｕ1＝ｕ＋ｋ(ｕ)*ｕ0

　

という形式の方程式で表現されなければならないと考えている。

　

以上の速度差及び合成速度に関する考察の結果、速度の概念が線形又は非線形に

関わらず、速度差は単純な２つの相対速度（観測者が直接観測する速度）の線形

の差（！）として表現されるという事が解る結果、非線形速度の合成の場合は、

現行の線形速度とは根本的に異なる扱いが必要となる。

これからは、考察の対象となる物理量が非線形の性質を有する速度という点に常

に注意しながら論理の展開を行わなければならない。

　

　以上の様な観点から、特殊相対性理論を再検討してみる。

手始めに、相対論のローレンツ収縮とは、「物質の運動の頭打ち現象」により、

運動中の物質の運動速度が低下する現象を、恰も物質（及び空間）がローレンツ

収縮と同等な数学上の見かけの短縮を生じる様に解釈している概念であり、一方、

物質の運動方向と逆方向を観ると、非線形速度の性質である線形の速度に比べて

速度が増加する現象を、恰も物質（及び空間）が数学上の見かけの伸張を生じる

（ローレンツ伸張と呼ぶ）事が想定される。

ローレンツ収縮率をα（＝√(１−(ｖ／ｃ)^2)）、ローレンツ伸張率をβとする。

　

この考えに基づき、線形の概念に於ける速度ｖで慣性運動中の全長２Ｌの列車の

先端と後端の光源から放射される光が列車の中央に達するまでの所要時間につい

て検討する。

尚、この思考実験は、アインシュタインが考えた任意の慣性座標系の三次元座標

の原点に設置している光源から放射された光の束が時間ｔと共に球面の状態で広

がる現象を想定すると、球面までの距離である√（ｘ^2＋ｙ^2＋ｚ2）が光の軌跡

であるｃｔに等しいとして２つの慣性座標系間の座標変換式を導く手法と本質的

には同等である。

なお、アインシュタインの思考実験は、光源に静止した慣性系と光源と或る速度

で運動している慣性系の２つを代表として選び、この慣性系同士の座標の変換を

考察しているが、光が運動している系を追い掛ける状態のみを考察の対象として

おり、光が逆向きの場合は考慮されていない事に注意する必要がある。

　

観測者が地上で観測している場合として考える。

列車が静止時に、先端と後端の光源から放射された光が列車の中央に到達する迄

にかかる所要時間は当然一致し、その時間をｔ0とすると、

　

ｔ0＝Ｌ／ｃ

　

次に、列車が一定の慣性系の速度ｖで運動中の場合を考える。

　

＜現行の解釈＞

列車の後端の光源から放射された光の所要時間ｔ1＝αＬ／（ｃ−ｖ）

列車の先端の光源から放射された光の所要時間ｔ2＝αＬ／（ｃ＋ｖ）

　

従って、ｔ1＝＞ｔ2であり、この矛盾を解消する為に、ｔ2の所要時間に、新たに、

時刻が異なるとして時刻差ｔ3を加えて、丁度、ｔ1＝ｔ2＋ｔ3となる様な同時刻

の相対性という条件を自然の基本性質に付加する事を必要としている。

また、光時計の思考実験に於いて、光の所要時間が丁度ローレンツ収縮率の逆数

に比例して延長するという考察を根拠に、時間の遅れを主張している。

　

＜新しい解釈＞

列車の後端から放射された光、即ち、運動の順方向へ向かう光の軌跡を考えると、

静止時に比べてその距離が延びる事は、その空間が静止時よりも引き延ばされた

状態（空間の伸張）を光が経験する事と等価であり、更に、物質の運動の頭打ち

現象、即ち速度が非線形に減少する性質を空間の収縮（ローレンツ収縮と同等）

として光が経験する事となり、この２つの相互の効果が相殺されて静止時と同じ

空間状態を光が経験する結果、静止時と同じ所要時間を要する事が可能となると

推定（非線形速度の前提条件）する。

これまでの推論で行った仮定は、下記の２つの項目（�T、�U）である。

　

(�T)非線形速度の性質の順方向の性質である「物質の運動の頭打ち現象」として

の速度の低下率が相対論のローレンツ収縮率と定量的に同じ事からの類推して、

非線形速度の順方向の性質として、物質の運動速度の低下を生じる現象と等価な

ローレンツ収縮と定量的に等しい数学上の架空の空間の収縮を想定する。

この現象を、非線形速度の基での新しい意味でのローレンツ収縮とする。

　

(�U)全ての慣性系の自然現象は同等であり区別出来ないという特殊相対性原理の

要請及び(�T)の仮定を用いて、

（ローレンツ収縮率）*（空間の伸張率）＝１（⇒静止時と同じ空間状態）と仮定。

　

　一方、列車の先端から放射された光、即ち、列車の運動の逆方向へ向かう光の

軌跡に於いては、静止時に比べてその距離が短縮する事は、空間が収縮した状態

（空間の収縮）を光が経験し、更に逆の方向に向かう光が経験する現象としての

非線形速度が線形速度に比べ増加する現象を、空間の伸張（ローレンツ伸張）と

仮定し、これら２つの相互効果が相殺されて、静止時と同じ空間状態を光が経験

する事となり、静止時と同じ所要時間を要する事が可能となると推定する。

これまでの推論で行った仮定は、下記の２つの項目（�V、�W）である。

　

(�V)非線形速度の逆方向の性質である線形速度に比べて速度が増加する現象を考

えると、(�T)の仮定の類推から、非線形速度の逆方向の性質としての速度の増加

と等価な数学上の架空の空間の伸張現象（ローレンツ伸張）が想定される。

　

(�W)全ての慣性系の自然現象は同等であり区別出来ないという特殊相対性原理の

要請及び（�V）の仮定を用いて、更に、(�U)との対称性を考慮して、

（ローレンツ伸張率）*（空間の収縮率）＝１（⇒静止時と同じ空間状態）と仮定。

　

以上の結果、任意の慣性系の任意の方向に向かう光の所要時間は静止時と等しく

一定に保たれている事が推定される事となり、任意の慣性系での電磁気現象に於

ける空間の対称性を保証する事（相対性原理の妥当性の確認）となる。

　

　ここで、以上の仮定の内容を論理的な矛盾が生じないか定量的に検討してみる。

手始めに、時間を不変に保つ事を可能とする非線形速度の性質をどの様な手段で

表現するかという問題がある。

四則演算が出来ない非線形の物理量を現行の線形代数学の範疇の手法で論理的に

導く事は不可能であるが、差し当たり、線形速度ｖをパラメータとする何らかの

関数の形で非線形速度の性質を表現する事が最初の試みとして適当と考える。

時間を不変に保つ為に必要な非線形速度の性質としては、ローレンツ収縮率αと

定量的に等価な性質の表現が不可欠である事となる。

　

＜列車の運動方向と同じ方向に向かう光の場合＞

先ず、列車が運動時に、列車の運動方向に向かう光について考える。

物質の運動の頭打ち現象という性質を備えた非線形速度の概念に於いて、列車の

速度をｕとして、これに対応する現行の線形速度の概念に於ける列車の速度をｖ

とする。

ここで、結果から述べると、列車の等速での運動状態を１つの慣性系と見なせば、

列車に固定された物質、つまり、列車がローレンツ収縮状態にあるとの相対論の

解釈を非線形速度の概念で考えると、列車がローレンツ収縮した状態を、速度の

非線形の性質による鈍化と捉えると、慣性系としての列車の速度ｖと列車の系に

固定された列車の真の速度である非線形速度（この速度をｕとする）とは異なる

（！）という事になる。

　

先ず、現行の線形速度の概念での列車の速度がｖの時の列車の後端から放射され

た光の所要時間をｔ1として、

　

ｔ1＝α*Ｌ／（ｃ−ｖ）

　

を、非線形速度の概念の導入の始めの現行の線形速度との関係の切っ掛けの式と

する。

ところで、相対論に於ける列車という慣性系の速度ｖと慣性系に静止した列車と

いう物体の速度は、当然ながら一致する事となる。

ところが、ローレンツ収縮が運動物体の運動方向の空間並びに物体の長さに掛か

る事を考慮すると、ローレンツ収縮こそは、慣性系の運動方向と順方向に向かう

光が体験する線形速度ｖの物体が非線形に速度が低下した状態を表現していると

解釈すると、この式の右辺の分子のαＬは、線形速度ｖで運動している物体の長

さがローレンツ収縮して短縮している状態の長さという事が元来の意味であるが、

この実際の意味は、線形速度ｖよりも低下した物体の真の非線形速度ｕ（今後、

線形速度をｖ、対応する非線形速度を明示的にｕとする）で運動している物体の

静止時と変わらない長さに相当していると解釈する事が出来る。

この様に考えると、この式の右辺の分母の光速ｃと線形の速度ｖの慣性系に静止

した物体の線形速度ｖとの速度差（ｃ−ｖ）は正しくない事となり、ｖの代わり

に物体の真の非線形速度ｕを充てるのが正しく、分母を（ｃ−ｕ）と変更しなけ

ればならない事となる。

よって、この式の右辺の分母の線形速度ｖを非線形速度ｕに置き換えて、

　

ｔ1＝α*Ｌ／（ｃ−ｕ）　･･･（Ｃ）

　

としてみる。

この式の右辺を変形させると、

　

ｔ1＝α*（ｃ／（ｃ−ｕ））*（Ｌ／ｃ）

　

この式の右辺は、(α；非線形速度の順方向に於ける収縮効果の割合)*（γ'≡

ｃ／（ｃ−ｕ）；光が経験する空間の伸張効果の割合)*（Ｌ／ｃ；長さＬの距離

を光が通過する際の所要時間）という意味合いとなり、

　

α*（ｃ／（ｃ−ｕ））＝１（⇒収縮も伸張もしていない静止状態の空間）

　

となる様に非線形速度ｕを決めると、ｔ1＝Ｌ／ｃとなり、静止時の光の所要時間

ｔ0と一致する事が可能となる。

　

上記の式をｕで解くと、

　

ｕ＝ｃ(１−α)

　＝ｃ(１−√(１−(v/c)^2))

　

この非線形速度ｕは、光速ｃを最大値（極大）とする円という２次関数になる。

更に、これをαで解くと、

　

ローレンツ収縮率α＝（ｃ−ｕ）／ｃ

　

となり、ローレンツ収縮の本来の意味が直観的に読み取れる。

又、この式をｖで解くと、

　

ｖ＝√ｕ（２ｃ−ｕ）

　

となり、ｕ≦ｖの関係にある事が分かる。

つまり、この非線形の速度ｕが、ローレンツ収縮効果にて、線形の速度ｖより常

に遅い速度で変化し、更に、光速ｃに近づくに連れて、円という二次間数の性質

に従い増加が抑えられる事により、「物質の運動の頭打ち現象」を発現している

事になると解釈できる。

ここで、列車の運動方向に向かう光が経験する空間の伸張の割合γ'は、

　

γ'≡ｃ／（ｃ−ｕ）＝１／α≡γ　（γ；ローレンツ因子）

　

運動している物体を追いかける光の軌跡の距離が伸びる事と等価の数学上の空間

の伸張の割合γ'がローレンツ因子γと定量的に等しい事となり、ローレンツ因子

の本来の意味が理解できる事となる。

　

＜列車の運動方向と逆の方向に向かう光の場合＞

　次に、列車の運動方向と逆の方向に向かう光の場合を考える。

順方向の場合と同様に考えて、非線形速度の概念での速度ｕ'で運動中の列車の

運動方向と逆の方向に向かう光の所要時間ｔ2は、ローレンツ伸張率βを使い、

　

ｔ2＝β*Ｌ／（ｃ＋ｕ'）

　

この式の右辺を順方向に向かう光の場合に習って変形させると、

　

ｔ2＝β*（ｃ／（ｃ＋ｕ'））*（Ｌ／ｃ）

　

逆方向に向かう光の軌跡が短縮する事と等価な数学上の空間の収縮の割合をδと

すると、上式の右辺は、（非線形速度の逆方向に於ける伸張効果の割合；β)*

(光が経験する空間の収縮効果の割合；δ＝ｃ/(ｃ＋ｕ'))*(長さＬの距離を光が

通過する際の所要時間；Ｌ/ｃ）という意味合いとなり、

　

β*ｃ／（ｃ＋ｕ'）＝１（⇒収縮も伸張もしていない静止状態の空間）

　

となる様に非線形の速度ｕ'を決めると、ｔ2＝Ｌ／ｃとなり、静止時の所要時間

ｔ0と一致する事が可能となる。

この式をβで解くと、

　

ローレンツ伸張率β＝（ｃ＋ｕ'）／ｃ

　

となり、ローレンツ伸張効果の意味が直観的に読み取れる事となる。

　

これまでの考察で、光速不変の原理及び特殊相対性原理の仮定の元で、新たに、

従来の速度の線形の概念に代わり、非線形の概念に変更して、(�T)〜(�W)の条件

の仮定の元で非線形速度の性質を決定すれば、光と物質の関わり合いが、任意の

慣性系で静止時と同等に行われる事が可能である事が分かった。

(�T)及び(�V)の仮定は非線形速度の新たな性質を想定するものであるが、今後の

更なる厳密な検討により、その妥当性を検証する事が必要となる。

また、(�U)及び(�W)の仮定は、非線形速度の概念を導入する事で初めて可能とな

る仮定（推定）であり、特殊相対性原理の要請から至極当然の推定であろう。

こちらも、今後の更なる厳密な検討で、その妥当性を検証する事が必要となる。

　

　非線形速度と線形速度との関係を巨視的に眺めると、現行の線形速度の基での

物体のローレンツ収縮の本来の意味は、慣性系の速度にローレンツ収縮率分低下

した速度が慣性系に静止した物体の真の速度であり、これこそ物体の非線形速度

に他ならない物であり、非線形速度の概念を導入した座標変換により時間を不変

に保つ事が可能となるのみならず、空間をも不変に保つことが可能となるものと

考える。

　

尚、順方向に向かう光の経過時間が静止時と同じとなる様に設定した非線形速度

ｕと逆方向に向かう光の所要時間が静止時と同じとなる様に設定した非線形速度

ｕ'とは同一の非線形の性質を持った速度でなければならない。

以下の考察でｕとｕ'が同一の非線形速度であることを証明する。

　

　ここで、素量子の運動状態式を振り返って観ると、従来の慣性系の線形速度ｖ

に対応する慣性系に静止している物体の真の非線形速度ｕが、

　

ｕ＝ｃ(１−√(１−(v/c)^2))

　

という関係式から、素量子の運動エネルギーの割合の係数が丁度、非線形速度と

光速ｃとの比であるｕ／ｃとなるが、この結果は運動エネルギーと非線形速度の

関係を考える上での良い示唆を与えるものと考える。

又、質量エネルギーの係数は（ｃ−ｕ）／ｃとなり、ローレンツ収縮率αと一致

し、この結果も何らかの示唆を与えるものと考える。

以上の結果、素量子の運動状態式は、下記の如く簡潔に表現する事が出来る事と

なる。

　

ε＝ｍ0*c*（ｃ−ｕ）　（素量子の質量エネルギーの項）

　 ＋ε*ｕ／ｃ　　　　（素量子の運動エネルギーの項）

　

この節の始めに導いた静止時の物質（ｎ0個の素量子の集合体）にエネルギーＥ１

（ｎ1個の素光子の集団）を与えて速度ｖ1に達した物質のｎ１とｖ1の関係式であ

るＢ式を下記に再掲する。

　

ｎ1／(ｎ0＋ｎ1)＝１−√(１−(ｖ1／ｃ)^2)

　

この式の右辺は、線形速度ｖ1に対応する非線形の速度ｕを光速ｃで除したもので

あるので、

　

ｕ＝ｃ*ｎ1／(ｎ0＋ｎ1)

　

この非線形速度ｕと与えたエネルギーの要素である素光子の個数ｎ1との関係は、

　

ｕ−ｃ＝−（ｎ0*ｃ）／（ｎ1+ｎ0）

　

となり、原点を（ｃ,-ｎ0)とする第４象限に於ける双曲線の性質を有する反比例

のグラフを描く事となる。

Ｃ節で述べた事柄を再掲すると、素量子の全エネルギーに対する質量エネルギー

の割合を示すα（ローレンツ収縮率に一致）と線形速度ｖの関係式は、

　

α＝√(１−(ｖ／ｃ)^2)

　

であり、この式のαとｖの関係は、楕円（ｃ^2*α＋ｖ^2＝ｃ^2）の第１象限に於

ける性質を持つ。

更に、非線形速度ｕと線形速度ｖは、

　

u＝ｃ(１−√(１−(v/c)^2))

　

∴(ｕ−ｃ)^2＋ｖ^2＝ｃ^2

　

の関係にあり、原点を（ｃ,0）とする第１象限での半径ｃの円のグラフを描く。

　

　ここで、この節の始めに導いた運動中の物質の運動方向に於ける速度の低下を

定量的に導いた式は、線形速度で展開したが、線形速度ｖに対応する非線形の順

方向の速度ｕと逆方向の速度ｕ'が求められたので、こちらを使用して改めてこの

非線形速度が同様な結果をもたらす事が出来るかを検討する事とする。

　

　Ｃ節の素量子の運動状態の方程式に於いて、運動エネルギーの項に着目して、

物質Ｓ（Ｍ0＝ｎ0*ｍ0）をエネルギーＥ1（＝ｎ1*ｅ）を順方向及び逆方向に加え

て加速した場合に、到達する速度を静止時と運動時に分けて比較し、その変化の

割合を検討する。

これまでの線形速度ｖを非線形速度ｕに置き換えて式を展開する。

　

Ｃ節で予想した従来の線形速度ｖに対応する新しい非線形速度ｕとの関係式は、

論理的に求めた訳ではあるが、漠然としたものであり、真の意味を掴む事に暫く

苦慮していた訳であるが、これ迄の考察の結果から、線形速度ｖで運動中の或る

慣性系に静止している物体の真の速度が、非線形速度ｕという事になる。

つまり、本来なら、慣性系の速度と慣性系に静止している物体の速度は、当然な

がら一致しなければならないが、線形速度の概念の基では、非線形速度の基本的

な性質である「物質の運動の頭打ち現象」をローレンツ収縮で代償させることで、

慣性系の座標変換の際に光速不変の原理を矛盾無く成立させる為の辻褄を合わせ

る事を行っていた訳であり、線形速度の概念の基では、慣性系の速度と慣性系に

静止している物体の真の速度は一致しないという驚くべき結果を得る事が出来る。

勿論、非線形の速度の概念の基では、慣性系の速度と慣性系に静止している物体

の速度は当然ながら厳密に一致する事となり、慣性系の線形速度ｖは実体を伴わ

ない架空の速度という結論を得る事となる。

　

ところで、線形の物理量を取り扱う事が可能な線形代数学という分野があるが、

非線形の物理量をダイレクトに取り扱うことが出来る現行の数学の手法は無い。

そこで、目下のところは、これまで述べた非線形速度ｕの性質を表す方程式の様

にして、線形速度ｖを媒介因子とする方程式の形で非線形速度ｕの性質を間接的

に表現する方法を採らざるを得ない。

そこで、非線形速度自体を変数としてダイレクトに演算したり方程式を立てたり

する手段が無いので、線形変数ｕを用いた関数で非線形速度の変数を肩代わりし

て、線形変数で可能な四則演算及び方程式を実現可能な手段を確立する事が必要

となる。

　

（Ａ）順方向

非線形速度ｕで運動中に、運動方向にエネルギーＥ1を与えた場合を検討する。

なお、線形速度と非線形速度は、

　

ｕ＝ｃ(１−√(１−(ｖ／ｃ)^2))、ｖ⇒ｕ、ｖ1⇒ｕ1、ｖ2⇒ｕ2

　

の対応とする。

　

（Ａ−１）静止時

与えたエネルギーＥ１（ｎ１個の素光子の集団）が全て物質Ｓの運動エネルギー

に変換されて速度ｕ1に達したとすると、エネルギー保存則により、

　

（与えたエネルギーＥ１）＝（物質Ｓの運動エネルギー）

　

であるので、

　

ｎ1*ε＝ｕ1*(ｎ0＋ｎ1)*ε／ｃ

　

∴ｎ1／(ｎ0＋ｎ1)＝ｕ1／ｃ　･･･ Ｂ1式

　

（Ａ−２）運動時

質量を有する全ての物質（素量子の集合体）の全エネルギーは、静止時と同一で

不変と仮定すると、非線形速度ｕで慣性運動中物質Ｓ（ｎ0個の素量子の集合体）

の状態式（慣性系の座標変換式に相当）は、

　

Ｓの全エネルギーＥ（不変）

＝（ｃ−ｕ）*ｎ0*ε／ｃ ･･･ 質量エネルギーの項

　　　　＋ｕ*ｎ0*ε／ｃ ･･･ 運動エネルギーの項

　

に於いて、その運動方向にエネルギーＥ1（ｎ1個の素光子の集団）を与えた時に、

物質Ｓの速度がｕ２に達したとすると、エネルギー保存則により、

　

ｕ*ｎ0*ε／ｃ　･･･　速度ｕで運動中の物質Ｓの運動エネルギー

＋ｎ1*ε　　　･･･　物質Ｓの加速に用いたエネルギーＥ1

＝ｕ2*(ｎ0＋ｎ1)*ε／ｃ ･･･ Ｅ1で加速した結果、速度ｕ2に

　　　　　　　　　　　 　　 達した物質Ｓの運動エネルギー

両辺を(ｎ0＋ｎ1)*ε／ｃで割ると、

　

ｕ*ｎ0／(ｎ0＋ｎ1)＋ｃ*ｎ1／(ｎ0＋ｎ1)＝ｕ2 ･･･ Ｃ1式

　

ここで、Ｂ1式より、

　

ｎ１／(ｎ0＋ｎ１）＝ｕ1／ｃ

　

及び

　

ｎ0／（ｎ0＋ｎ１）＝(ｃ−ｕ1)／ｃ

　

を用いてＣ1式に代入して、ｎ0とｎ1を消去すると、

　

ｕ(ｃ−ｕ1)／ｃ＋ｕ1＝ｕ2

　

∴ｕ2−ｕ＝ｕ1*(ｃ−ｕ）／ｃ･･･ Ｄ1式

　

Ｄ1式の左辺は、非線形速度ｕで運動中の物質に運動方向にエネルギーＥ1を加え

て物質を加速させて、非線形速度ｕ２に達した場合の速度差（ｕ2−ｕ）を表し、

右辺は物質の静止時に加えられたエネルギーＥ1により加速された非線形速度ｕ1

が、非線形速度ｕでの運動時には、

　

(ｃ−ｕ）／ｃ倍(＝ローレンツ収縮率；α＝√(１−(ｖ／ｃ)^2))

　

に変化（鈍化）した事を表している。

　

また,非線形速度ｕで運動中の物質に併走する慣性系で観た場合に、その順方向に

エネルギーＥ1を加えた場合は当然、物質の非線形速度はｕ1として観測されるが、

元の慣性系で観ると、物質の非線形速度がｕ2となった訳であり、この非線形速度

ｕ2は、非線形速度ｕと非線形速度ｕ１の速度の加法則の解を意味し、

　

ｕ2＝ｕ＋ｕ1*(ｃ−ｕ）／ｃ･･･ Ｆ1式

　

この右辺は、非線形速度ｕで運動中の物質の速度が非線形速度の順方向の性質の

現れであるローレンツ収縮効果で低下した非線形速度ｕ1で加算された速度と解釈

出来る。

つまり、非線形速度の加法則は、線形速度の加算の形式で表現できるのに対して、

線形速度の概念を前提とする相対論の速度の加法則は、実際の非線形速度の性質

を表現する必要性から、逆に非線形速度の加算の形式が必要となる理屈である。

次に、Ｄ1式を変形すると、

　

（ｃ−ｕ2）／ｃ＝（（ｃ−ｕ）／ｃ）*（（ｃ−ｕ1）／ｃ） ･･･ �T式

　

�T式の左辺は加速してｕ2の非線形速度に達した場合の非線形速度の順方向の性質

であるローレンツ収縮率を表し、右辺は加速前の非線形速度ｕ時の非線形速度の

順方向の性質であるローレンツ収縮率に非線形速度ｕ1時の非線形速度の順方向の

性質であるローレンツ収縮率を掛けた式である。

つまり、非線形速度ｕ時の非線形速度の順方向の性質の現れとしてのローレンツ

収縮率が運動方向と順方向にエネルギーを加えて非線形速度ｕ1に達した場合に、

非線形速度の順方向の性質であるのローレンツ収縮率に変化した場合のその比は、

非線形速度ｕ1での非線形速度の順方向の性質であるのローレンツ収縮率に一致す

るという事を意味している。

　

（Ｂ）逆方向

つぎに、非線形速度ｕで運動中に、運動方向と反対方向にエネルギーＥ1を与えた

場合を考察する。

なお、仮に、非線形速度ｕ'の性質を、

　

ｕ'＝ｃ(１−√(１−(v/c)^2))

　

の方程式で表現出来ると仮定し、線形速度と非線形速度は、

　

ｖ⇒ｕ'、ｖ1⇒ｕ1'、ｖ2⇒ｕ2'

　

の対応とする。

　

（Ｂ−１）静止時

与えたエネルギーＥ１が、全て物質Ｓの運動エネルギーに変換されて非線形速度

ｕ1に達したとすると、エネルギー保存則により、

　

（与えたエネルギーＥ１）＝（物質Ｓの運動エネルギー）

　

であるので、

　

ｎ1*ε＝ｕ1*(ｎ0＋ｎ1)*ε／ｃ

　

∴ｎ1／(ｎ0＋ｎ1)＝ｕ1／ｃ　･･･ Ｂ2式

　

（Ｂ−２）運動時

非線形速度ｕ'で慣性運動中の物質Ｓ（ｎ0個の素量子の集合体）に、運動方向と

反対方向にエネルギーＥ1を与えた場合に、物質Ｓの非線形速度がｕ2'に達したと

すると、エネルギー保存則により、

　

ｕ*ｎ0*ε／ｃ　･･･　非線形速度ｕで運動中の物質Ｓの運動エネルギー

−ｎ1*ε　　　･･･　物質Ｓの減速に用いたエネルギーＥ1

＝ｕ2*(ｎ0＋ｎ1)*ε／ｃ ･･･ Ｅ1で減速した結果、非線形速度がｕ2に

　　　　　　　　　　　 　　 達した物質Ｓの運動エネルギー

両辺を(ｎ0＋ｎ1)＊ε／ｃで割ると、

　

ｕ*ｎ0／(ｎ0＋ｎ1)−ｃ*ｎ1／(ｎ0＋ｎ1)＝ｕ2' ･･･ Ｃ2'式

　

ここで、Ｂ2式より、

　

ｎ１／(ｎ0＋ｎ1）＝ｕ1'／ｃ

　

及び

　

ｎ0／（ｎ0＋ｎ１）＝(ｃ−ｕ1')／ｃ

　

を用いてＣ2'式に代入して、ｎ0とｎ1を消去すると、

　

ｕ'(ｃ−ｕ1')／ｃ−ｕ1'＝ｕ2'

∴ｕ'−ｕ2'＝ｕ1'*(ｃ＋ｕ'）／ｃ･･･ Ｄ2'式

　

このＤ2'式の左辺は、非線形速度ｕ'で運動中の物質Ｓに、運動方向と反対方向に

エネルギーＥ1を加えて物質Ｓの運動速度を減速させて非線形速度ｕ2'になった時

の速度差(ｕ'−ｕ2')を表し、右辺は、物質Ｓの静止時にエネルギーＥ1で達した

非線形速度ｕ1'が非線形速度ｕ'で運動時には、

　

(ｃ＋ｕ'）／ｃ倍（＝ローレンツ伸張率；β＝２−√(１−(ｖ／ｃ)^2))

　

に増加している事を表している。

この結果は、光の思考実験に於ける非線形速度の逆方向の性質の現れである

ローレンツ拡張効果の予想を定量的に裏付けるものである。

　

更に、この結果は、

　

ｕ'＝ｃ(１−√(１−(v/c)^2))

　

と仮定した事の妥当性を示している。

つまり、光の順方向の所要時間が静止時と同じになる様に決めた非線形速度ｕと

光の逆方向の所要時間が静止時と同じになる様に決めた非線形速度ｕ'とは、同一

の非線形速度であり、ｕで統一して、

　

ｕ＝ｃ(１−√(１−(v/c)^2))

　

となる。

つまり、任意の慣性系での光と物質の関わり合いでの所要時間が、任意の方向で

静止時と変化無く不変であると仮定すれば、現行の線形速度の概念の基に於ける

線形速度ｖの慣性系に静止した物質の非線形速度の概念の基での真の非線形速度

ｕとの関係式が、

　

ｕ＝ｃ(１−√(１−(v/c)^2))

　

で表現できる事が証明された。

以上の結果は、非線形速度の概念の仮定が自然の真理の追求の方向が正しい方向

を向いている事を確信させるものであり、万一間違った方向に向かっているとす

れば、極めて奇跡的な偶然であると言わざるを得ない。

改めて、

　

ｕ'＝ｕ、ｕ1'＝ｕ1、ｕ2'＝ｕ2

　

として、Ｄ2'式を書き直すと、

　

ｕ−ｕ2＝ｕ1*(ｃ＋ｕ）／ｃ･･･ Ｄ2式

　

又、非線形速度ｕで運動中の物質の反対方向に、物質と併走する慣性系で観て、

その非線形速度がｕ1となる様にエネルギーＥ1を加えて、物質の速度を減速させ

た場合に達した物質の非線形速度ｕ2は速度の加法則の解を意味し、Ｄ2式でｕ2を

解くと、

　

ｕ2＝ｕ−*(ｃ＋ｕ）／ｃ･･･ Ｆ2式

　

この右辺は、非線形速度ｕで運動中の物質の速度が、非線形速度の逆方向の性質

の現れであるローレンツ伸張効果で修飾された非線形速度ｕ1で減速された速度と

解釈出来る。

つまり、Ｆ2式は、逆方向の非線形速度の加法則を表している事になる。

Ｆ2式で、光が逆方向に向かうという事で、ｕ＝−ｃ又はｕ1＝−ｃで成立する様

に変形すると、

　

ｕ2＝ｕ＋*(ｃ＋ｕ）／ｃ

　

更に、上式で、ｃを−ｃに置き換えると、

　

ｕ2＝ｕ＋*(−ｃ＋ｕ）／−ｃ

∴ｕ2＝ｕ＋*(ｃ−ｕ）／ｃ

　

となり、Ｆ1式で、ｃを−ｃに置き換える事で、逆の方向へ向かう光の場合（ｕ＝

−ｃ又はｕ1＝−ｃ）も成立する事が可能となり、汎用性を持たせる事が出来る。

また、Ｄ2式を変形すると、

　

（ｃ＋ｕ2）／ｃ＝（（ｃ＋ｕ）／ｃ）*（（ｃ−ｕ1）／ｃ） ･･･ �U式

　

となり、�U式の左辺は、減速してｕ2の速度に低下した時のローレンツ伸張率を表

し、右辺は減速前の速度ｕ時のローレンツ伸張率に速度ｕ1時のローレンツ収縮率

を掛けた式である。

つまり、速度ｕで運動中の物質に、減速する方向にエネルギーを加えた場合に、

その減速率が速度ｕ1の時のローレンツ収縮率に一致するという事を意味している。

以上の結果を纏める。

　

光が順方向に向かう場合（ｕ＝ｃ又はｕ１＝ｃ）の非線形速度の加法則は、

　

ｕ2＝ｕ＋ｕ1*(ｃ−ｕ）／ｃ･･･ Ｆ1式

　

尚、光が逆方向に向かう場合（ｕ＝−ｃ又はｕ１＝−ｃ）は、Ｆ1式で、ｃを−ｃ

に置き変えて下記の式に変更する事で成立する。

　

ｕ2＝ｕ＋ｕ1*(ｃ＋ｕ）／ｃ･･･ Ｆ2式

　

これ迄、光と物質の関わり合いに関する考察や、物質にエネルギーを与えた場合

の速度が任意の慣性系でどの様に変化するかを考察してきたが、その結果、光の

思考実験で、(�T)〜(�W)の条件の仮定の元で非線形速度の性質を決定すれば、光

と物質の関わり合いが、任意の慣性系で静止時と同等に行われることが可能であ

る事が解った。

この非線形速度の概念の基では、物質の加速効果が光の思考実験の予想を裏付け

る結果を得て、非線形速度の概念に於ける光に関する速度の加法則を導き出す事

が出来たものと考える。

　

D節＞非線形速度の加法則に関する任意の物体への拡張の検討

　ここで、任意の慣性系に於ける光以外の物質の運動に関する思考実験を考える。

光の思考実験では、地上から観て、列車と光の関わり合いを考察したが、この度

は、光の代わりに模型の車の運動状態が、地上の観測者の立場で、慣性系の運動

状態に依りどの様に変化するかを考察する。（以下の速度は全て非線形の速度）

列車が静止時に、模型の車をｕ0の速度で列車内の後端と先端から列車の中央に向

けて同時に発車したとすれば、地上の観測者は、列車が静止時と速度ｕで運動中

の場合とでは、いずれの場合でも車同士が正面衝突する場所は列車の中央の位置

として観測しなければならない。

　

列車の全長を2Ｌとすると、列車が静止時に列車の後端及び先端から同時に出発し

た車が列車の中央まで移動するのに要する所要時間は、当然ながら一致する事と

なり、この時間をｔ0とすれば、

　

ｔ0＝L／ｕ0

　

（列車の運動方向と順方向への模型の車の運動）　

速度ｕで運動中の列車の後端から出発した列車が、列車が静止時にｕ0の速度の車

の合成速度ｕ1は、列車の運動の順方向に向かう為に、光が順方向に向かう場合の

非線形速度の加法則を利用して、

　

ｕ1＝ｕ＋ｕ0*（ｃ−ｕ）／ｃ ･･･ Ｇ1式

　

このＧ1式を、光以外の物体の順方向の非線形速度の加法則の候補としてみる。

順方向に向かう車が列車の後端から列車の中央部（長さＬ）に到達する迄の所要

時間をｔ1とすると、慣性系の運動方向への空間及び物体のローレンツ収縮は無い

（空間の不変性）という事で、Ｌは不変として、

　

ｕ1*ｔ1＝ｕ*ｔ1＋Ｌ

　

この式に、Ｇ1式よりｕ1を代入して、ｔ1で解くと、

　

（ｕ＋ｕ0*（ｃ−ｕ）／ｃ）ｔ1＝ｕ*ｔ1＋Ｌ

ｕ*ｔ1＋ｕ0*ｔ1（（ｃ−ｕ）／ｃ）＝ｕ*ｔ1＋Ｌ

∴ｔ1＝（Ｌ／ｕ0）＊（１／（（ｃ−ｕ）／ｃ））

　

ここで、線形速度の概念に於ける慣性系の速度をｖとし、慣性系に静止している

物体の真の非線形速度をｕとした場合のｖとｕの関係式が、

　

ｕ＝ｃ（１−√(１−(ｖ／ｃ）^2)）

　

である事から、

　

１／（ｃ−ｕ）／ｃ＝１／√(１−(ｖ／ｃ）^2)≡γ　（γはローレンツ因子）

　

である事に注意すると、

　

ｔ1＝（Ｌ／ｕ0）*（１／（（ｃ−ｕ）／ｃ））

　　＝ｔ0*γ

　

となり、列車の順方向に運動中の車の所要時間ｔ1は静止時の所要時間ｔ0よりも

γ倍の割合だけ延長する事となり、非線形速度の概念に於ける慣性運動中の物体

の運動の鈍化の割合が相対論の時間の遅れと定量的に一致する事が解る。

つまり、相対論では経過時間がγ倍延長する事を時間の遅れと解釈している事に

対して、非線形速度の概念の基では、経過時間の延長は物体の運動自体の鈍化が

原因である事が証明された事になる。

この結果は、言うまでも無く、これまでの全ての実験結果と一致する事となる。

　

以上の結果にて、Ｇ1式は光以外の質量を有する任意の物体にも適用できる順方向

の非線形速度の加法則として使用可能と判断する。

尚、本来は、非線形速度を表す方程式を基に、光以外の質量を有する任意の物体

にもＧ1式が適用できる事を数式の展開で論理的に導く必要がある。

　

（列車の運動方向と逆方向への模型の車の運動）

列車の先端から列車の中央に向けて列車の静止時に速度ｕ0で出発した車は、ｕの

速度で運動中の列車の運動方向と逆方向に向かう為に、この状態の車の合成速度

ｕ2を非線形速度の逆方向の加法則を利用して求める事とする。

　

ここで、光の場合の逆方向の非線形速度の加法則を仮に利用すると、

　

ｕ2＝ｕ−ｕ0*（ｃ＋ｕ）／ｃ ･･･ Ｇ2式

　

この逆走する車が列車の先端から列車の中央部（長さＬ）に到達するまでの所要

時間をｔ2とすると、慣性系の運動方向への空間及び物体のローレンツ収縮は無い

（空間の不変性）という事で、Ｌは不変として、

　

ｕ2*ｔ2＝ｕ*ｔ2−Ｌ

　

この式に、Ｇ2式よりｕ2を代入して、ｔ2で解くと、

　

（ｕ−ｕ0*（ｃ＋ｕ）／ｃ）ｔ2＝ｕ*ｔ2−Ｌ

ｕ*ｔ2−ｕ0*ｔ2（（ｃ＋ｕ）／ｃ）＝ｕ*ｔ2−Ｌ

∴ｔ2＝（Ｌ／ｕ0）＊（１／（（ｃ＋ｕ）／ｃ））

　　 ＝ｔ0*（１／（（ｃ＋ｕ）／ｃ））

　

となり、ｔ2は、順方向の所要時間ｔ1とは明らかに異なる結果、列車の中央部で

衝突する事が出来ない事となり、実際の現象とは矛盾する結果となる。

そこで、逆方向の速度を合成する場合の質量を有する物質の振る舞いは光の場合

とは異なるのではないかと考えざるを得なくなる。

そこで、Ｇ2式で、ｕ0の係数（（ｃ＋ｕ）／ｃ ）を未知変数ｋに置き換えて、

　

ｕ2＝ｕ−ｕ0*ｋ ･･･ Ｇ0式

　

この逆走する車が列車の先端から列車の中央部（長さＬ）に到達するまでの所要

時間をｔ2とすると、

　

ｕ2*ｔ2＝ｕ*ｔ2−Ｌ

　

この式に、Ｇ0式よりｕ2を代入して、ｔ2で解くと、

　

（ｕ−ｕ0*ｋ）ｔ2＝ｕ*ｔ2−Ｌ

ｕ*ｔ2−ｕ0*ｔ2*ｋ＝ｕ*ｔ2−Ｌ

∴ｔ2＝（Ｌ／ｕ0）／ｋ

　 　＝ｔ0／ｋ

　

ここで、列車の中央で２つの車が正面衝突する為の必要条件は、ｔ2＝ｔ1であり、

　

ｔ1＝ｕ0*γ＝（Ｌ／ｕ0）／ｋ

　

と置いて、ｋで解くと、

　

ｋ＝１／γ＝α＝（ｃ−ｕ）／ｃ

　

これを、Ｇ0式に代入して、

　

ｕ2＝ｕ−ｕ0*（ｃ−ｕ）／ｃ ･･･ Ｇ3式

　

となり、Ｇ3式は、Ｇ1式に於いて逆方向の運動という事で、ｕ0を−ｕ0に置き換

えた式と一致する事になる。

但し、Ｇ2式が質量を有する物質の場合は成立しない事を、本来は非線形の速度の

性質を表す方程式を基に、数式の展開で論理的に導かなければならない。

　

これ迄の考察の結果、Ｇ1式の速度の加法則のみで順方向と逆方向の速度の加法則

を統一する事が出来る事となる。

　

任意の物質の非線形速度の加法則；ｕ1＝ｕ＋ｕ0*（ｃ−ｕ）／ｃ　･･･ Ｇ1式

　

但し、光が逆方向に向かう場合（ｕ＝−ｃ又はｕ0＝−ｃ）は、上式のｃを−ｃに

置き換えて、

　

ｕ1＝ｕ＋ｕ0*（−ｃ−ｕ）／−ｃ

　 ＝ｕ＋ｕ0*（ｃ＋ｕ）／ｃ

　

に変更する事で、光の場合の逆方向の非線形速度の加法則が成立する事となる。

　

以上により、運動中の列車の後端から中央部までを順方向に運動する模型の車の

所要時間ｔ1と運動中の列車の先端から中央部までを逆方向に運動する模型の車の

所要時間ｔ2は、列車の静止時に比べて何れもγ倍の割合で所要時間が延びて列車

の中央で正面衝突する事となる。

これで、慣性運動中の列車の任意の方向に運動する物体は、列車が静止時に比べ

て、１／γ倍に運動が鈍化することが予想される事となり、回転運動を行ってい

る物質の回転速度も同じく１／γ倍に鈍化する事が予想される。

この現象は、物質の振動状態（周期運動）にも当てはまり、振動の周期がγ倍に

延長する現象（振動数としては、逆数の１／γ、つまりα倍に低下する）として

観測される事が予想される。

以上の予想される現象は、運動物体の時計（時間では無い！）の遅れや動く光源

から放射された光の横ドップラー効果等のこれまでの全ての観測事実と定量的に

一致する。

なお、慣性系が静止状態での回転運動が滑らかであれば、運動状態でも滑らかな

運動として観測されなければならないが、その為には、任意の方向の運動の鈍化

が一様に生じる必要性があり、速度の鈍化を表現する任意の方向の速度の加法則

がＧ1式のみで達成できるという事も、人知を遙かに越えた自然の摂理の絶妙さに、

改めて驚嘆し、畏敬の念を禁じ得ない。

　

ここで、非線形速度の概念の基での現在も未解決（懸案）の有名な現象（双子の

パラドックスと本質的には同じ現象）を挙げておく。

宇宙線が大気圏に突入する際に大気の成分粒子と衝突してミュー粒子が生成され

て地上に向けて亜光速ｖで運動する反応がありますが、地上の慣性系で観測した

場合に、相対論的効果を考慮しない場合は地上の実験室でのミュー粒子の半減期

Ｔ0よりもミュー粒子が生成された時点から地上までの到達時間ｔ0（＝Ｌ0／ｖ；

Ｌ0を地上までの距離）が長い（ｔ0＞Ｔ0）ために、地上に到達する前に崩壊して

ミュー粒子を観測する事が論理的に不可能となるが、相対論的効果として亜光速

ｖで運動中のミュー粒子の半減期Ｔ1がＴ0よりもγ倍延長（Ｔ1＝γＴ0＞ｔ0）す

る結果、実際の観測事実として、ミュー粒子を地上で観測する事が出来る事とな

る。

この現象を亜光速ｖで運動中のミュー粒子に固定した慣性系で考ると、当然なが

ら、半減期Ｔ0で崩壊する結果、到達時間ｔ0より半減期Ｔ0が短い（ｔ0＞Ｔ0）為

に、ミュー粒子が崩壊する前に地上に到達する事は不可能となる。

この一見すると矛盾する現象を、相対論では速度ｖで運動中のミュー粒子に固定

した慣性系では、ミュー粒子が生成した地点から地上までの距離Ｌ0がローレンツ

収縮する（Ｌ＝αＬ0）事で、地上までの到達時間ｔがローレンツ収縮率αの割合

で短縮（ｔ＝Ｌ／ｖ＝αＬ0／ｖ＝αｔ0）する結果、到達時間ｔが半減期Ｔ0より

も短く（Ｔ0＞ｔ＝αｔ0）なり、地上まで崩壊せずに到達する事が可能となると

解釈されている。

　

但し、この解釈は対称的（相対的）な論理展開とは言い難く、ローレンツ収縮で

解決しようと意図すれば、地上の観測機器に固定した慣性系でミュー粒子の観測

に於いてもローレンツ収縮効果を考慮する事が必要となり、亜光速ｖで運動中の

ミュー粒子から観測機器迄の距離Ｌ0がローレンツ収縮効果で短縮（Ｌ＝αＬ0）

する事で、到達時間ｔ（αｔ0）が半減期Ｔ0よりも短く（ｔ＝αｔ0＜Ｔ0）なる

事で観測事実を説明しなければならないと考える。

ところが、相対論的効果に於いては、時間の遅れ（具体的には経過時間がγ倍に

延長）はローレンツ収縮（具体的には、距離がα倍に短縮）とは並立の状態で生

じると解釈されているので、地上の慣性系での観測結果では、ミュー粒子が更に

長い距離(γＬ0）を運動しても崩壊しない事が予想される事となり、結局亜光速

で運動中のミュー粒子に固定した慣性系での観測結果との定量的な整合性が取れ

なくなると考える。

一方、非線形の速度の概念では、ローレンツ収縮など生じない事から、この現象

を矛盾無く説明する事は、目下のところは出来ない。

但し、非線形の速度の概念の基の物体の運動の鈍化の効果が相対論のローレンツ

収縮効果と等価と解釈すれば、辻褄合わせができない訳ではない。

例えば、地上での観測で非線形の速度ｕで運動中のミュー粒子を観測する場合に、

非線形の速度の性質としての運動の鈍化の効果によるミュー粒子の崩壊速度が、

１／γ、即ちα倍に低下している状態を観測する事は、運動の鈍化が生じていな

い（ミュー粒子が半減期Ｔ0で崩壊）状態で、ローレンツ収縮効果にて、αＬ0に

短縮した空間を運動する事と等価であると解釈する方法がある。

すると、非線形の速度ｕで運動中のミュー粒子に固定した慣性系で観測する場合

は、崩壊の半減期はＴ0ですが、地上の観測機器までの距離Ｌ0がローレンツ収縮

すると仮定すれば、地上の観測機器までの距離がαＬ0に短縮する事で、到達時間

ｔ0がα倍に短縮される（ｔ＝αｔ0）結果、半減期Ｔ0以内に観測機器に到達する

事が出来る（Ｔ0＞ｔ＝αｔ0）という解釈になる。

蛇足であるが、ミュー粒子に固定した慣性系に於いて、地上の慣性系（速度ｕで

ミュー粒子に接近して来ている）を観測する場合は、地上の実験室のミュー粒子

の半減期は、物体の運動の鈍化の効果にてγ倍に延長して観測されるが、ミュー

粒子と地上の観測機器の空間がローレンツ収縮すると仮定すれば、物体の運動の

鈍化の効果は無くなり、地上の実験室でのミュー粒子の半減期は、ミュー粒子が

静止時と同じくＴ0として観測される事となる。

　

以上の考察の結果を基本に立ち返って考えると、慣性系同士の現象は、相対的

（対称的）な現象であり、結果が非対称な現象となる為には、何らかの絶対的な

他の要因が加わらなければならない事に注意すべきである。

つまり、これまでの考察の様に、慣性系同士の現象をどの様にこねくり回したと

ころで、非対称な結果であるミュー粒子を地上で検出出来る様に論理展開する事

は不可能であるという事になる。

そこで、可能性のある要因を考えると、ミュー粒子が生成されて亜光速に加速さ

れる過程でミュー粒子の崩壊速度が鈍化する作用が生じる可能性や、ミュー粒子

が大気圏を亜光速で運動している過程で大気の成分との相互作用により減速され

る事でミュー粒子の崩壊速度が鈍化する可能性や、ミュー粒子が検出器に捕捉さ

れる際の減速過程でミュー粒子の崩壊速度が鈍化する可能性という３つの要因が

考えられる。

但し、検出器で減速される前にミュー粒子が崩壊していれば、時間が逆転する事

など不可能な為にミュー粒子を検出出来ない事は当然であり、最後の要因は除外

されなければならない。

結局、ミュー粒子の生成過程（亜光速迄の加速効果）と大気圏を亜光速で運動中

（減速効果）に、ミュー粒子の崩壊速度が絶対的に鈍化する可能性がある事にな

る。

なお、運動物体が加速や減速を受ける際は、一般相対性理論の等価原理により、

重力場に置かれた運動物体の時間の遅れ（非線形の速度の概念の基では、物体の

運動の鈍化）が絶対的に生じる事と同様な効果が生じる事を論拠としている。

更に、ミュー粒子が地球の重力場を自由落下という加速運動によるミュー粒子の

崩壊速度の低下も無視できないかも知れない。

あとは、以上の考察の結果を厳密に定式化し、実際の観測値を代入して、地上で

ミュー粒子を検出する事が可能となるかシミュレーションする事で、懸案事項が

決着される事になる。

　

D節＞非線形速度の妥当性の検証実験の提案

　ここで、これまでの物理学の常識が覆る可能性がある事柄を述べる。

線形速度の概念を前提とする特殊相対性理論に於ける速度の加法則は、

　

ｖ1＝（ｖ＋ｖ0）／（１＋ｖ＊ｖ0／ｃ^2）

　

であり、ｖ0＝−ｖの場合は、車の速度はｖ1＝0という静止状態として観測される

事となり、線形速度の概念に基づくガリレイ変換の場合も同様な結果を得る。

この結果は、これまでに自明の理と考えられてきた事柄である。

一方、非線形速度の加法則で、ｖ０＝−ｖに対応するｕ0＝−ｕの場合は、

　

ｕ1＝ｕ＋ｕ0*（ｃ−ｕ）／ｃ

　 ＝ｕ−ｕ*（ｃ−ｕ）／ｃ

　 ＝ｕ^2／ｃ

　 ≠0

　

となり、ｕ0＝−ｕの場合は、何と！、車の速度は慣性系の運動方向にｕ^2／ｃの

速度で運動している事となる。

これは、非線形速度の性質から、慣性系で逆走する物体の非線形速度ｕ0が慣性系

が運動時には、静止時よりも鈍化する事からの必然的な帰結となる。

この現象は、学生の物理実習程度の簡単な実験で確かめる事が出来るものと考え

る。

この実験は、非線形速度の概念の正当性を検証する実証実験として極めて重要で

あり、現行の特殊相対性理論の線形速度の概念との正否の決着を付ける為にも、

是非必要な実験と考える。

　

この実際の検証実験の一案として、高速走行中の列車の先端から列車の進行方向

と逆の方向に列車の速度と同じ光源となる物体を動かして、地上で光源から発し

た光の周波数の静止時との変化の割合を測定（光のドップラー効果）し、諸々の

誤差の範囲を超えて非線形の速度の場合の予測値に優位に一致するか否かを検証

する事で、正否を決着する事ができると考える。

問題は、現在の列車の速度は５００ｋｍ／ｈ程度が上限であり、この速度で誤差

の範囲を優位に超える測定値を得る事が理論的に出来るかどうかという事になる。

更にもう一つの実証実験案としては、ほぼ真空な宇宙空間に於いて、慣性運動中

のロケットの進行方向と逆の方向にロケットと同じ速さの光源となる物体を宇宙

空間に発射して、地上の観測装置でこの光源から放射された光の周波数を測定す

るという実験も比較的容易に実施できるのではないかと考える。

　

ところで、運動中の列車の系で、逆方向に列車と同じ速度で模型の車を動かすと、

地上と模型の車は同一の速度で観測されるので、模型の車は地上に静止している

様に観測される事となり、非線形速度の概念の矛盾点では無いかという鋭い意見

が出ている。

目下の所、この指摘（非線形速度のパラドック）に対する正しい回答を見い出す

には至っていない。

　

D節＞非線形速度の概念の纏め

　以上の結果は、(�T)〜(�W)の仮定の元での非線形速度を規定し、それを用いた

光と物質の関わり合いが任意の慣性系で同一の現象としてシミュレーション可能

である事が証明される。

更に、この非線形速度の概念を用いると、物質と物質の関わり合いに於いても、

任意の慣性系で静止時に比べてγ倍に時間経過が増加する事が分かり、この現象

を、相対論では時間自体の遅延効果と解釈していることに対して、非線形速度の

概念の基では、非線形速度の性質である物質の運動自体の鈍化が原因であるもの

と結論付ける事が出来る。

　

ここで、新しく定義した非線形速度の効果及び空間の効果について纏めておく。

任意の慣性運動中の座標系での光の所要時間が静止時と等しく不変であると仮定

すると、慣性系の線形速度ｖとこの慣性系に静止した物質の真の非線形速度ｕと

の関係式は、

　

ｕ＝ｃ(１−√(１−(v/c)^2))

　

（１）ローレンツ収縮効果、ローレンツ収縮率；α＝（ｃ−ｕ）／ｃ

これは、非線形速度の性質の運動方向の現れである物質の運動の頭打ち現象その

ものであり相対論のローレンツ収縮と定量的に一致する為に、アインシュタイン

に敬意を表して、その名称をそのまま拝借しているが、その内容は全く異なる。

但し、運動している物質の運動方向への加速効果の低下が元来の現象であるが、

数学上の架空の空間の収縮効果に例えても成立すると考えると、この架空の現象

は、相対論のローレンツ収縮と内容的にも一致する事となる。

なお、オリジナルのローレンツ収縮は、ローレンツがマイケルソン・モーレーの

光の媒質であるエーテルに対する地球の相対速度を検出する目的の実験結果であ

る相対速度ゼロを説明する為の論理的予想（エーテルの圧力による物質の収縮）

に付けられた名称であるが、アインシュタインが特殊相対性理論を構築する際に

導き出した空間の収縮と定量的に一致する事で、ローレンツに敬意を表する意味

で、その名称ををそのまま受け継いだものである。

ところで、物質Ａとそれに連れて運動している物質Ｂの関わり合いを別の視点で

考えると、物質Ａの速度が光速に近づくに連れて、物質Ａの運動方向に進む物質

Ｂの速度が非線形速度の順方向の性質の現れであるローレンツ収縮率と同じ割合

で低下すると共に、物質Ａの進行方向の空間がローレンツ収縮率で短縮を生じる

事は、恰も、順方向の空間が短縮されている様な効果を生じている事から、この

現象を非線形速度の順方向の性質に起因する「非線形速度の収縮効果」と呼ぶ事

とする。

この効果を力学的に説明すると、或る速度ｕで運動中の物体を構成している原子

の運動は、運動方向にはローレンツ収縮率でその速度が低下している訳であり、

この結果、原子から構成されている物体、更には系全体が運動方向にローレンツ

収縮率で収縮している事と等価の現象をもたらしていると解釈する事が出来る。

勿論、何らかの原因で力学的な外力により物質自体が収縮するという事では無い。

尚、この効果は、物理現象を遠くから観察した場合に、距離と速度が共に縮小し

た様に観測される事に似た現象という事で、「非線形速度の遠視効果」と呼ぶ事

とする。

非線形速度による空間の収縮効果が、運動している物体に付随して動作している

物質の運動の鈍化を生じさせている原因であろう。

　

（２）ローレンツ伸張効果、ローレンツ伸張率；β＝（ｃ＋ｕ）／ｃ

これは、非線形速度の性質の運動方向と反対方向での現れであり、物質の運動の

頭打ち現象の反対の効果と考える。

ところで、相対論では運動方向と反対方向の効果は考慮されておらず、該当する

既存の概念が無く、ローレンツ収縮の反対の効果で、素光子説独自の造語である。

この現象は、元来は、運動中の物質の運動方向と反対の方向にエネルギーを与え

て物質の速度を減速した場合の減速効果の増加の現象であるが、数学上の架空の

空間の伸張効果に例えても成立すると考える。

ところで、物質Ａとそれに連れて運動している物質Ｂの関わり合いを別の視点で

考えると、非線形速度の逆方向の性質の現れとしてのローレンツ伸張率に比例し

て物質Ｂの速度が増加すると共に空間もローレンツ伸張する現象は、非線形速度

の逆方向の性質に起因する「非線形速度の伸張効果」と呼ぶ事とする。

尚、この効果は、物理現象を近くから観察した場合に、距離と速度が共に拡大し

た様に観測される事に似た現象という事で、「非線形速度の近視効果」と呼ぶ事

とする。

この効果を力学的に説明すると、或る速度ｕで運動中の物体を構成している原子

の運動は、非線形速度の逆方向の性質であるローレンツ伸張率でその速度が増加

している訳であり、この結果、原子から構成されている物体、更には、系全体が

運動方向と逆方向にローレンツ伸張率で伸張している事と等価の現象をもたらし

ていると解釈する事が出来る。

勿論、何らかの原因で力学的な外力により物質自体が伸張するという事では無い。

　

（３）空間の伸張効果、空間の伸張率；γ＝ｃ／（ｃ−ｕ）

これは、運動中の物質の運動方向に向かう光の軌跡が静止時に比べて伸びる現象

と等価な数学上の架空の空間の伸張効果で、光と物質の速度差（ｃ−ｕ）の比と

なる。

なお、この値がローレンツ収縮率と逆数の関係にある為に、物質の運動方向に向

かう光は、ローレンツ収縮効果と空間の伸張効果を同時に経験する結果、任意の

慣性系に於いて、光は静止時と同じ空間状態を経験し、その所要時間も静止時と

変わらず不変となる。

尚、空間の伸張率βとローレンツ因子γ（１／√(１−(v/c)^2)）が定量的に一致

する。

　

（４）空間の収縮効果、空間の収縮率；δ＝ｃ／（ｃ＋ｕ）

これは、運動中の物質の運動方向と反対の方向に向かう光が経験する、数学上の

架空の空間の拡張効果であり、常に光速ｃで運動している光にとっては、空間が

恰も収縮している状態を経験する事に相当し、光と物質の速度差（ｃ＋ｕ）の比

となるが、相対論では運動方向と反対方向の効果は考慮されておらず、該当する

既存の概念が無く、素光子説独自の新しい概念である。

尚、この値がローレンツ伸張率と逆数の関係にある為に、物質の運動方向と逆の

方向に向かう光は、ローレンツ伸張効果と空間の収縮効果を同時に経験する結果、

任意の慣性系に於いて、光は静止時と同じ空間状態を経験することとなり、その

所要時間も静止時と変わらず不変となる。

ここで、一つ注意すべき事柄は、相対論のローレンツ収縮（空間の収縮）と紛ら

わしい名称ではあるが、その内容や値は全く異なる事に注意したい。

　

この節での考察の結果を総括すると、素量子の運動状態式は、現行の座標変換式

を含めた力学の内容を凌駕する多くの重要な自然の基本法則を内包している事が

推測されるが、見方を変えると、この方程式が自然現象をシミュレートする最も

基本的な方程式の１つでは無いかという確信を強める事となり、更なる基本法則

の発見に繋がる解析を行う必要があると考える。

　

ここで、�T式と�U式を再掲する。

　

（順方向）（ｃ−ｕ2）／ｃ＝（（ｃ−ｕ）／ｃ）*（（ｃ−ｕ1）／ｃ）　�T式

（逆方向）（ｃ＋ｕ2）／ｃ＝（（ｃ＋ｕ）／ｃ）*（（ｃ−ｕ1）／ｃ）　�U式

　

�T式と�U式は、共に速度ｕで運動中の物質に順方向と逆方向に一定のエネルギー

を与えて速度がｕ2に変化した場合に、�T式の場合はローレンツ収縮の変化の割合、

また、�U式の場合はローレンツ伸張の変化の割合が、共に速度ｕ1の非線形速度の

順方向の性質の表れであるローレンツ収縮率に一致する事を表している。

つまり、非線形速度の順方向と逆方向の性質の表れとしての或る物理量の変化の

割合が一致する因子（ｕ1の速度のローレンツ収縮率）を見つけた事を意味する。

これで、相対論の時間の遅れに相当する物質の運動の鈍化の原因の解明が完成し

たものと考える。

　

尚、ついでに付け加えると、相対論の列車の床と真上の天井に設置している鏡の

間を反射しながら光が往復する光時計の思考実験も、列車が運動中は、光の軌跡

が常に列車の進行方向に向かっている為に、静止時の上下に往復する光の軌跡よ

り常に長い距離を進む事となり、これをもって運動中は時間が遅れていると判断

しているが、例えば、列車の床から進行方向と反対の方向で適当な距離を隔てて

天井に鏡を置き、静止時に正しく光が反射を繰り返す様に調整したとすると、或

る速度で運動時には、床から放射された光の軌跡が丁度真上に向かう様に調節す

る事も出来る事となり、この場合は静止時より運動時の方が光の軌跡が短くなり、

光時計の実験とは反対に時間が速く進む様に解釈される事となるが、更に、天井

から床に光が向かう場合は、列車の進行方向に光が向かう為に、光の軌跡が延長

する事となり、時計が遅れる様に観測されるという、光の向かう方向に依存して、

時間が遅くなったり速くなったりするという明らかな矛盾を孕んでいる事であり、

少なくとも、光時計の思考実験は列車の進行方向に向かう光の軌跡の延長だけで

時間の遅れと断定している事は、甚だ片手落ちの思考実験と言わざるを得ない。

つまり、相対論の光時計の思考実験は、素量子の集合体である質量を有する全て

の物質の運動状態に於いて、運動方向に加速する場合だけで時間の遅れと同等な

物質の運動の鈍化を断定した素光子説の判断の過ちと同類のものであると考える。

相対論の光時計の思考実験で矛盾を回避できる唯一の方法は、素光子説と同様に、

光の往復時間は往路も復路も静止時と同じであると仮定する事だけと考えるが、

線形性速度の概念上では速度の増加と減少とは量的に対称であり、一見すると、

容易に実現可能の様に思われるが、逆に、順方向と逆方向の速度差を無くすため

には、どうしても速度に非線形の性質を導入しなければ解決できない事であり、

相対論では、逆の方向の考察は行わず、アインシュタインの同時刻の相対性とい

うミラクル処方により、順方向と同じく逆方向もローレンツ収縮が生じていると

仮定する事で全ての現象を矛盾無く論理展開する事が可能となった事はラッキー

でもあり、長い目で観ればアンラッキーであったと考える。

なお、列車の床及び直上の天井の設置した鏡の間を往復する光の軌跡は鮫の歯様

の光の軌跡を描き、真上よりも後方に設置した鏡の間の光の往復は、鋸の歯様の

光の軌跡を描く事を付け加えておく。

　

ここで、列車の床とその直上の天井に鏡を設置して、その間を光が反射しながら

往復する光時計の思考実験の時間の遅れに関し定量的に検討してみる。

動く列車を地上で観測しているものとする。

列車が静止時に床から天井までに光が到達する時間をt、速度ｖで動く列車内での

前上方に進む光の所要時間をt'とすると、有名な直角三角形のピタゴラスの定理

により、

　

(ct')^2 = (ct)^2 + (vt')^2　・・・（Ａ）

　

光時計の思考実験で、列車が静止時は、床と直上の天井の鏡の間を光が反射しな

がら往復する。

このときの光の軌跡は、（Ａ）の右辺の第一項のｃｔである。

列車が速度ｖで運動中は、床から放射された光は列車の速度とのベクトルの合成

で、斜め上前方に向かう。

先ず、光時計の光が斜め前上方に向かう有名な模式図の問題点は、初めから時間

の遅れが生じていると決めつけて、その時間の遅れを定量的に求めるという手法

を採っている事にある。

従って、（Ａ）は時間の遅れを前提とした式であり、その結果は、時間が遅れな

ければ式が成立しない事になるのは、当然という事になる。

　

そこで、今回は、t＝t`を前提として（Ａ）を見直してみる。

ここで、この様な状態を空間が引き延ばされた状態を光が感じるという表現で表

すと、この空間の伸張の割合がローレンツ因子γ(1/√(１−(v/c)^2))と一致する。

この観点から、（Ａ）を眺めてみる。

（Ａ）の左辺で、静止時の光の軌跡がctであり、これが列車の運動により空間が

引き延ばされたと同じ効果にて、

　

ct'＝ct／√(１−(v/c)^2）

　

と置くことが出来るものと考える。

又、（Ａ）の右辺の第一項は静止時と運動時は変化が無いのでそのままであるが、

第二項は、これも空間の伸張を考えて、

　

vt'＝vt／√(１−(v/c))^2)

　

と置くことが出来ると考える。

これらを総合して、この式を（Ａ）に代入すると、

　

{ct/√(１−(v/c)^2)}^2＝(ct)^2＋{vt/√(１−(v/c)^2)}^2　・・・（Ｂ）

　

となるが、（Ｂ）が恒等的に成立しているか判定する為に、左辺と右辺の差を取

ると、

　

（左辺）−（右辺）

＝{ct/√(１−(v/c)^2)}^2−(ct)^2−{vt/√(１−(v/c)^2)}^2

＝t^2{(c^2−v^2)/(１−(v/c)^2)−c^2}

＝0

　

となり、確かに（Ｂ）は任意の時間tと速度vで恒等的に成立している事が分かる。

　

つまり、空間の伸張を考慮すれば、t'＝tの条件で、光の思考実験の直角三角形で

のピタゴラスの定理の式を満足する事が出来る事となる。

また、見方を変えれば、（Ａ）を解けば、

　

t'＝t/√(１−(v/c)^2）

　

という時間の遅れの解が求まり、これを（Ａ）に代入した式が（Ｂ）そのものと

いう事になる。

相対論は、これを時間の遅れと解釈しているのに対し、非線形速度の概念に於い

ては、時間の遅れは無いという前提であり、（Ｂ）の左辺は、ctという静止時の

光の軌跡の空間が速度ｖで運動する結果、引き延ばされてγが付加されたと解釈

し、右辺の第二項は、vtという距離の成分に注目し、静止時はゼロ(v＝0)である

が、速度ｖで運動する結果、こちらも空間が引き延ばされた（γの付加）と解釈

する事が出来る。

さて、列車が運動する結果として、空間が伸張した効果が生じるが、更に、運動

する物体に非線形速度の順方向の効果としてローレンツ収縮効果が加わり、空間

の伸張効果であるローレンツ因子γ(1/√(1-(v/c)^2))にローレンツ収縮率α

（√(１−(v/c)^2))が掛かる為に、２つの効果が打ち消し合う結果、静止状態の

空間に等しくなるという事になる。

実際の式では、（Ｂ）の左辺のct及び右辺の第二項のvtにローレンツ収縮率α

(√(１−(v/c)^2))が加わり、

　

{(ct/√(１−(v/c)^2)}×√(１−(v/c)^2))^2

＝(ct)^2＋{(vt/√(１−(v/c)^2)}×√(１−(v/c)^2))^2

　

となるが、静止状態の空間に於いて、上の右辺の第二項に関しては、v⇒０となり、

　

(ct)^2＝(ct)^2＋0

∴ct＝ct

　

即ち、運動時の光の軌跡（左辺のct）と静止時の光の軌跡（右辺のct）が恒等的

に等しくなる事が分かる。

　

余談ではあるが、相対論でも、時間の遅れ(ローレンツ因子;1/√(1-(v/c)^2）が

空間の伸張に相当するので、これにローレンツ収縮率(√(1-(v/c)^2))が加わると、

２つの効果が相殺されて、時間の経過が静止時と等しくなると解釈する道は残さ

れていると考えるが、ローレンツ変換の解で、時間の遅れが絶対的な事実として

決定されている為に、この様に解釈する事が出来なかったものと考える。

また、慣性系の速度をｖとしてピタゴラスの定理が成立する直角三角形の場合は、

　

（斜辺の長さ）−（底辺の長さ）

　＝ｃ−√（c^2−v^2）

　＝ｃ(1-√(1-(v/c)^2))

　≡ｕ（慣性系の線形速度vに対応する慣性系に静止した物質の真の速度ｕ）

　

となり、これが慣性系の速度ｖからローレンツ収縮効果分としての速度の鈍化を

差し引いた速度ｖの慣性系に静止している物質の真の速度を表している事となる。

　

特殊相対性理論が誕生して早くも約１世紀が経過したが、これ迄に相対論的効果

に矛盾を見出そうとするパラドックスが数多く提出されてきたが、矛盾を指摘す

る疑問点が悉く否定されて、相対論的効果を支持する実験結果を併せて、盤石の

基盤を築いている事は周知の通りである。

ところで、２００６年の４月に、「車輪のパラドックス」という運動する物体の

時間の遅れが実際の運動の遅れに関与するか否かという自然現象の本質的な問題

を提起するこれ迄に提出された事が無いタイプのパラドックスが提出された。

　

＜車輪のパラドックス＞

列車の車輪の回転速度に於いて、車輪の円周の表面速度（線速度）が列車の速度

に一致する。

そこで、或る速度で運動中の列車を地上から観測したとすると、動く物体の時間

が遅くなる様に観測されるので、列車の慣性系の時間が遅くなり、車輪の回転数

も低下するので、結局、列車の速度も低下しなければならなくなる。

という事は、列車が運動する限り、時間の遅れという強力無比のブレーキ効果に

て車輪の回転速度が低下する結果、論理的には、列車は少しも動くことが出来な

くなるという事になる。

勿論、この様な現象は実際は生じていない。

つまり、「運動物体の相対的な時間の遅れは本当に生じているのであろうか？」

というパラドックスである。

　

この問題提起に対する或る解決策は、列車の系で車輪とレールとの接点での車輪

の線速度が列車の速度と等しいとする、一見すると当然と思われる設定を行い、

これを地上の系に座標変換すると、列車の速度に依存して時間の経過が遅くなる

事となり、車輪の回転周期が延長し車輪の回転速度も低下する様に考えられるが、

車輪とレールとの接点に於ける車輪の線速度が列車の速度と同じく一定値を保っ

ているという条件（つまり、線速度と地面に固定されているレールの相対速度は

ゼロ！の為に時間の遅れが生じない！）がそのまま生きている為に、車輪の回転

周期が延長するにも拘わらず、車輪とレールとの接点での車輪の線速度は列車の

速度と同じ状態で変化しないという事になり、矛盾が生じる事は無い。

但し、そのしわ寄せというべき車輪の角速度にムラが生じるという異常な結果が

生じる事となった。

この現象は、周期運動している全ての物体に適応される相対論的効果の二次的な

効果である。

天体の自転や公転を観測する系に依存して周期運動にムラが生じる現象が、果た

して生じている事実が観測されているのであろうか？

ここで、列車の車輪のレールとの接点に於ける線速度は、列車の速度と一致する

事となるが、車輪とレールが接しているからと言っても、線速度と車輪が接して

いるレールの相対速度がゼロである事は無い。

もしも、これが正しいとすると、列車の速度とレールつまり地面との相対速度が

ゼロとなり、列車は地面に対して動いている場合も動いていないという矛盾を生

じる事を意味する事となる。

　

ところが、非線形速度の概念の基では、列車の速度と列車に静止した物質の速度

は一致する為に、或る速度で運動している列車の車輪のレールとの接点の線速度

は、列車の速度と当然ながら一致する結果、列車の速度と列車に静止した物質の

速度の関係と同等となり、相対論的効果の様な列車という慣性系と慣性系の物質

の時間の遅れ（つまり、物質の運動の鈍化）に起因する列車と車輪の運動の乖離

の現象など生じる事は無い。

　

D節＞非線形速度に基づいた慣性系の座標変換方式の創出の試み

最後の段階として、非線形速度の概念を導入した慣性系の座標変換式を求める事

とするが、座標変換を達成する前に立ちはだかる一見すると越え難いハードルを

明確にしておく。

慣性系の座標変換は、２つの慣性系間の相対速度に応じた時間と空間（距離）を

因子とする変換であるが、一次変数同士の変換（一次変換）で無ければならない

事が論理的に要求される。

そこで、ガリレイ変換及びローレンツ変換は、各々の因子に未知変数を付加して、

連立一次方程式を立てて未知変数を解く事で座標変換式を求める事が出来る。

この方法を踏襲して、非線形速度の概念を導入した座標変換を求めようとすると、

必然的にローレンツ変換と同じ座標変換式にならざるを得ない事となり、はたと

絶望のどん底に陥る事となる。

ところが、冷静に判断すると、非線形速度という非線形の数を導入する段階で、

現行の線形代数の手法（この場合は連立一次方程式）は適用できない事が解る。

そこで、慣性系の座標変換の原点である時間と空間を不変量にするガリレイ変換

及びローレンツ変換に於いて、速度を非線形に変えるだけの変更から再出発する

事を試みて、解決すべき問題点を明確にする事が、非線形速度の概念を導入した

座標変換を達成する近道と考える。

　

慣性系の線形速度ｖと慣性系に静止した物体の真の非線形速度ｕという限定され

た２つの物理量の関係を表す方程式（ｕ＝ｃ(１−√（１−(v/c)^2))から、現行

の線形速度の概念を取り去ることで、汎用的で一般的な非線形速度の性質を表す

方程式となる事が出来る。

　

＜線形速度と非線形速度の性質を表す方程式＞

光速をｃ、速度の次元を持ち正の実数で光速ｃが上限のパラメータをθ、無次元

の単位ベクトルをｋとする。

　

現行の線形速度　；ｖ＝ｙ（θ、ｋ）＝θｋ

新しい非線形速度；ｕ＝ｙ（θ、ｋ）＝ｃｋ（１−√(１-(θ／ｃ)^2))

　

非線形速度ｕはｘｙ座標で中心が（０，ｃ）で半径がｃの円の３／２π〜２πの

部分を描き、線形速度ｖは非線形速度ｕが描く円の部分の円弧に張る弦に相当す

る。

ここで余談であるが、弦が線形速度ｖのグラフであり、一方、非線形速度が円弧

を描くイメージから、非線形変数を象徴する固有文字として、日本語の片仮名で

ある「ノ」を充てる事を提案したい。

非線形速度の変数ｕの表記法は、明示的に、その直前に全角の「ノ」又は半角の

「ﾉ」を付加して、

　

明示的な非線形速度；ノｕ＝ｙ（θ、ｋ）＝ｃｋ（１−√(１-(θ／ｃ)^2))

　

ガリレイ変換での線形速度が無限大まで可能との考えと非線形の速度が光速ｃを

極限値として２次関数（円）的に変化する事が物理的に等価の効果を生じている

と考えると、直観的には、無限大に伸びている直線（線形速度）をギューッと押

し縮めて曲線（円）にしたのが、非線形速度になるというイメージである。

　

なお、現実の問題として運動中の物体の速度を実測してｖ0であった場合に、この

速度は線形か非線形かどちらの速度と判断すべきかという素朴な疑問が生じるが、

現行の線形速度ｖの前提の基てはｖ＝ｖ0と解釈し、非線形速度ｕの前提の基では

ｕ＝ｖ0と解釈する事となる。

ここで、線形速度ｖと非線形速度ｕの間には数値的な大小関係として常にｖ≧ｕ

の関係があるが、これをどの様に解釈すべきかという素朴な疑問が生じる。

線形速度の概念の基での実測値ｖ＝ｖ0は、これは確かに紛れもなく物体の速度で

あるが、速度ｖ0で運動中の物体に固定された慣性系という慣用的な表現で慣性系

の速度が決定されているが、ローレンツ変換を巨視的に眺めると、実は速度ｖ0は

慣性系の速度では無い事に気付く事となる。

つまり、運動中の物体は運動方向にローレンツ収縮していると解釈されているの

で、ローレンツ収縮の効果分の物体の速度の低下が実際は生じている事となり、

このローレンツ収縮に依る速度の低下分を考慮した物体の線形速度が、物体の真

の速度である非線形速度と一致する事となる。

この結果、運動している物体に固定された慣性系の速度と物体その物の速度とは

異なるという事になり、ローレンツ変換に関して言えば線形速度ｖは一般的には

慣性系の速度を指している訳であり、慣性系に静止している物体の真の速度を指

している訳では無いという事である。

つまり、現行の線形速度ｖは慣性系の速度の事であり、非線形速度ｕは物体その

物の速度という事になり、ｖ≧ｕの関係にある事となる。

なお、ガリレイ変換や非線形速度を導入した新しい座標変換は、ローレンツ収縮

の様な空間の収縮などが無い事に依り、慣性系の速度と慣性系に静止した物体の

速度は一致する事となる。

ところで、非線形速度ｕを導出する際のこの速度ｕに対応する線形の速度ｖは、

全て慣性系の速度の事であり、慣性系に静止している物体の実際の速度では無い

事に留意する必要がある。

つまり、これ迄の非線形速度ｕと、この性質を表す方程式で使用されている線形

速度ｖというパラメータの関係は、慣性系の線形速度ｖとこの慣性系に静止した

物体のローレンツ収縮により生じた速度の低下分を差し引いた真の非線形速度ｕ

との関係を表した関係式とみるのが本質的な解釈である。

　

　古来からニュートン力学の時代を経て１９世紀末の光速不変性の発見までを、

線形速度の概念の時代とし、光速不変の原理を前提とする特殊相対性理論が発表

された１９０５年から今日までの約１世紀（２０世紀）を速度の概念を線形から

非線形に変更する過渡期の時代とすれば、２１世紀は非線形速度の概念が完成し、

科学の大発展が期待される時代という事が出来る。

今にして思う事であるが、過渡期としての特殊相対性理論が無ければ、古来より

自明と考えられてきた線形速度の概念を、光速不変性の発見のみで非線形速度の

概念に変更する事は不可能であったろうという感想を持っている。

ニュートン力学から過渡期としての特殊相対性理論に於ける慣性系の線形速度と

その慣性系に静止状態（慣性系の速度と等しい速度）の物質のローレンツ収縮の

状態の物体の線形速度という関係のお膳立てが無ければ、直接ガリレイ変換から

非線形速度の概念を導入した座標変換を直ちに達成する事は出来なかった訳であ

り、速度の概念の大変革（有史以来の科学の大革命）には特殊相対性理論の登場

が必要不可欠であったものと考える。

なお、速度の概念を冷静に振り返って観ると、元々、速度とは物体の運動の程度

の目安として定量的に考え出された物理量であり、自然に存在している物理量で

は無い事に気付くべきである。

つまり、速度という物理学で最も重要な物理量が線形であるべき物理学的な根拠

など皆無であり、先人が素朴な直感力で線形に変化する物理量に違いないと決め

たに過ぎないという事である。

　

相対性原理とは、「互いに運動する物体の座標系の間では、物理学の法則が不変

な形を保つ」という原理であるが、非線形速度の概念の基での新しい座標変換で

は、文字通りの相対速度以外の基本的な物理量（時間や空間や質量）は不変を保

つことが出来る事になり、ガリレイ変換に準じた結果をもたらしている。

ところで、慣性系の座標変換に於いて暗黙の了解事項としては、任意の慣性系に

固定された観測者は、物理現象を完全に同一の現象として観測するという事柄が

前提となっていると考えると、現行の相対性原理の内容は証明可能な事柄が主体

であり、後者の前提は証明する事が原理的に不可能と考えられる為に、こちらを

相対性原理と呼ぶ事が相応しいと考える。

また、Ｃ節での素量子の運動状態式は、時間発展の基で求められる方程式であり、

これを座標変換にも拡張する事が可能かどうかも証明が困難な状況にあり、この

「時間発展に於ける素量子の運動状態式が座標変換にも適用出来るとする原理」

を新しい意味での相対性原理に含める事も必要と考える。

　

（１）ガリレイ変換（速度は線形で、無限大まで許容）

　

　　（前提）線形の速度、速度の無限大性の許容、ガリレイの相対性原理

　

　　慣性座標系Ｋ（ｘ,ｙ,ｚ,ｔ）に対し,時間ｔ＝0でお互いの系の観測者の原点

　　が一致して速度ｖでｘ軸方向に運動中の慣性座標系Ｋ'（ｘ',ｙ',ｚ',ｔ'）

　　は、

　

　　ｘ'＝ｘ−ｖｔ

　　ｙ'＝ｙ

　　ｚ'＝ｚ

　　ｔ'＝ｔ

　

　　線形速度の加法則；ｖ2＝ｖ±ｖ1

　　速度が線形で無限大まで許容される為に、加減算が可能である。

　

（２）ローレンツ変換（速度は線形で、光速ｃが上限）

　

　　（前提）線形の速度、光速不変の原理、特殊相対性原理

　

　　慣性座標系Ｋ（ｘ,ｙ,ｚ,ｔ）に対し,時間ｔ＝0でお互いの系の観測者の原点

　　が一致して速度ｖでｘ軸方向に運動中の慣性座標系Ｋ'（ｘ',ｙ',ｚ',ｔ'）

　　を考える。

　　アインシュタイン流の座標変換式の導出法に準じて進める。

　　２つの慣性系の共通の原点に設置されている光源から光が放射された瞬間を

　　時間ゼロとしてそれぞれの座標系の経過時間をｔ、ｔ'とする。

　　光の到達距離ｃｔ、ｃｔ'は、光速不変の原理にて、

　　Ｋで観測する光の速度がｃ ⇒　(ｃｔ)^2＝ｘ^2＋ｙ^2＋ｚ^2　　　（Ａ）

　　Ｋ'で観測する光の速度がｃ⇒　(ｃｔ')^2＝ｘ'^2＋ｙ'^2＋ｚ'^2　（Ｂ）

　　座標変換が一次変換で表される事が必要という条件から、

　

　　ｘ'＝γ（ｘ−ｖｔ）　　　　　　　　　　　　　　　　　　　　　（Ｃ）

　　ｔ'＝γ（ａｔ＋ｂｘ）　　　　　　　　　　　　　　　　　　　　（Ｄ）

　

　　以上の（Ａ）、（Ｂ）、（Ｃ）、（Ｄ）から、未知数γ、ａ、ｂを解くと、

　　下記の座標変換式が得られる。

　　ここで、注意すべきは、式（Ｄ）の時間の変換式にｂｘが付加されている事

　　であり、これは、一見すると奇異に思われるが、運動している物体を追い掛

　　ける光の所要時間は静止時より長くかかり、物体に向かう光の所要時間は短

　　くなるという極常識的な判断から予想される同時刻の相対性の概念の必要性

　　を表している。

　

　　ｘ'＝γ（ｘ−ｖｔ）

　　ｙ'＝ｙ

　　ｚ'＝ｚ

　　ｔ'＝γ（ｔ−ｘ*ｖ／ｃ^2）

　

　　ただし、ローレンツ因子γ＝１／√(１−(ｖ／ｃ)^2)であり、これは非線形

　　速度の概念を導入する際に行った光が経験する思考実験に於ける物質の運動

　　方向に向かう光が経験する空間の伸張率と定量的に一致する。

　　なお、変換式の中核を成す係数γがｖ⇒ｃの極限では無限大に発散する事は、

　　数学的には許容されても、自然を対象とする物理学には馴染めないと考える。

　

　　線形速度の加法則；ｖ2＝（ｖ±ｖ1）／（１±ｖ*ｖ1／ｃ^2）

　

　　＊ローレンツ変換に於ける速度の加法則は、正に非線形速度の存在を示唆

　　している式と解釈される。

　

（３）ローレンツ変換に於ける速度を線形から非線形に変えた座標変換方式

　

　　（前提）速度を線形から非線形に変更、光速不変の原理、相対性原理

　

　　非線形速度ｕ（＝ｋｃ(１-√(１-(θ/ｃ)^2))）を導入する。

　　但し、ｋを速度の単位ベクトルとして、θ（0≦θ≦ｃ）を線形の変数とする。

　　尚、ローレンツ変換の公式を求める連立一次方程式（線形の変数で構成）を

　　解く手法では、座標変換式の公式を求める事は不可能な為に、非線形速度に

　　は、元々光速不変の原理が織り込み済みであり、又、予め確認している時間

　　と空間の不変性を条件とする事で、連立一次方程式を解く過程を回避する事

　　が可能となる。

　

　　慣性座標系Ｋ（ｘ,ｙ,ｚ,ｔ）に対し,時間t＝0でお互いの系の観測者の原点

　　が一致して速度ｕでｘ軸方向に運動中の慣性座標系Ｋ'（ｘ',ｙ',ｚ',ｔ'）

　　は、

　

　　ｘ'＝γ（ｘ−ｕｔ）

　　ｙ'＝ｙ

　　ｚ'＝ｚ

　　ｔ'＝γ（ｔ−ｘ*ｕ／ｃ^2）

　

　　ここで、非線形速度ｕの性質である任意の慣性系での物理現象の経過時間が

　　一定（ｔ'＝ｔ）となり、同時刻の相対性も無用の概念となる為に、ｔ'のｘ

　　の項が消失する結果、ｔ'＝γｔとなるが、ｔ'＝ｔの為に、γ＝１となり、

　　結局、速度を非線形に変更したローレンツの座標変換式は下記になる。

　

　　ｘ'＝ｘ−ｕｔ

　　ｙ'＝ｙ

　　ｚ'＝ｚ

　　ｔ'＝ｔ

　

　　＜非線形速度の加法則＞

　　ｕ2＝ｕ＋ｕ1*(ｃ−ｕ）／ｃ

　

　　但し、ｕ＝−ｃ又はｕ0＝−ｃの場合は、ｃを−ｃに置き変えて、

　　ｕ1＝ｕ＋ｕ0*（ｃ＋ｕ）／ｃ

　　を使用する必要がある。

　

　　以上の結果、ガリレイ変換で線形速度ｖを非線形速度ｕに置き換えた変換式

　　と同じとなったが、非線形速度の性質である時間と空間の不変性がガリレイ

　　変換と同じ事を考えると、当然の帰結と考える。

　　更に、変換式では表現できない非線形速度の空間に関する性質の補足事項と

　　して、下記の４つの性質を合わせて座標変換を実行する事が必要である。

　

　　１．ローレンツ収縮効果、ローレンツ収縮率；α＝（ｃ−ｕ）／ｃ

　　２．ローレンツ伸張効果、ローレンツ伸張率；β＝（ｃ＋ｕ）／ｃ

　　３．空間の伸張効果、空間の伸張率；γ＝ｃ／（ｃ−ｕ）

　　４．空間の収縮効果、空間の収縮率；δ＝ｃ／（ｃ＋ｕ）

　

　尚、慣性座標系間の座標変換に於いて、一次変換が成立する為の論理的な必要

条件が線形速度を前提としなければならないという事であれば、現行のガリレイ

変換やローレンツ変換に準じて非線形速度を導入して新しい慣性系の座標変換を

構築する事は不可能という事になる。

そこで、慣性座標系間の座標変換が一次変換でなければならない事は自明である

が、速度の非線形の導入に際して、どの様に折り合いを付けて一次変換式を達成

出来るかが最後の課題と考える。

（３）の試案では、線形速度と光速不変の原理及び特殊相対性原理を前提とした

ローレンツ変換を叩き台として、この変換式で非線形速度を導入した場合に生じ

る現象としての時間の不変性から変換式を修正したものである。

本来は、非線形速度の概念を前提として座標変換の際に光速不変性を前提として

方程式を立てる事が必要ではあるが、非線形速度の性質を方程式にダイレクトに

表現する事が意外と容易でないと思われるので、今回の座標変換式の導出過程は

姑息的でスマートさに欠ける嫌いがあるが、先ずは、一案を提示できた事で満足

したい。

ここで、もう一つの非線形速度を導入した座標変換式の導出方法を示す。

　

（４）非線形速度を導入した新しい慣性系の座標変換方式の試案

　

　　（前提）非線形速度、光速不変の原理、相対性原理

　

　　非線形速度ｕ（＝ｋｃ(１-√(１-(θ/ｃ)^2))）を導入する。

　　但し、ｋを速度の単位ベクトルとして、θ（0≦θ≦ｃ）を線形の変数とする。

　　尚、ローレンツ変換の公式を求める連立一次方程式（線形の変数で構成）を

　　解く手法では、座標変換式の公式を求める事は不可能な為に、非線形速度に

　　は、元々光速不変の原理が織り込み済みであり、又、予め確認している時間

　　と空間の不変性を条件とする事で、連立一次方程式を解く過程を回避する事

　　が可能となる。

　

　　慣性座標系Ｋ（ｘ,ｙ,ｚ,ｔ）に対し,時間t＝0でお互いの系の観測者の原点

　　が一致して速度ｕでｘ軸方向に運動中の慣性座標系Ｋ'（ｘ',ｙ',ｚ',ｔ'）

　　を考えると、座標変換式は、時間と空間の不変性によりガリレイ変換に準じ

　　て、

　

　　ｘ'＝ｘ−ｕｔ

　　ｙ'＝ｙ

　　ｚ'＝ｚ

　　ｔ'＝ｔ

　

　　なお、変換式自体に非線形速度の全ての性質をダイレクトに表現することが

　　出来ないので、座標変換の付帯事項として下記の４つの非線形速度の性質を

　　併用する事が必要である。

　

　　１．ローレンツ収縮効果としてのローレンツ収縮率；α＝（ｃ−ｕ）／ｃ

　　２．ローレンツ伸張効果としてのローレンツ伸張率；β＝（ｃ＋ｕ）／ｃ

　　３．空間の伸張効果としての空間の伸張率；γ＝ｃ／（ｃ−ｕ）

　　４．空間の収縮効果としての空間の収縮率；δ＝ｃ／（ｃ＋ｕ）

　

　　＜非線形速度の加法則＞

　　ｕ2＝ｕ＋ｕ1*(ｃ−ｕ）／ｃ

　　

　　但し、ｕ＝−ｃ又はｕ0＝−ｃの場合は、ｃを−ｃに置き変えて、

　　ｕ1＝ｕ＋ｕ0*（ｃ＋ｕ）／ｃ

　　を使用する必要がある。

　

　　非線形速度を導入した結果、相対性原理はガリレイの相対性原理に近似する

　　内容となる。

　

ここで、

仕上げの段階として、非線形速度の概念を導入した慣性系の座標変換を考察する。

慣性座標系Ｋ（ｘ、ｙ、ｚ、ｔ）と時間ｔ＝0で原点が一致して速度ｕでｘ軸方向

に運動中の慣性座標系Ｋ'（ｘ'、ｙ'、ｚ'、ｔ'）を考えて、時間ｔ＝0で原点に

ある光源から光が四方八方に放射されたとすると、

　

Ｋ系から観たｔ秒間にｘ軸方向に進んだ光の軌跡　 ；ｘ＝ｃt　　 ･･･（Ａ）

Ｋ'系から観たｔ'秒間にｘ'軸方向に進んだ光の軌跡；ｘ'＝ｃt' 　･･･ (Ｂ）

時間の不変性；ｔ'＝t

　

慣性系の運動方向と順方向及び逆方向に運動している物体の座標変換を考える。

　

（慣性系の運動方向（速度ｕの方向）と順方向に向かう物体の座標変換）

順方向に向かう物体の場合の座標変換式を考える。

光の場合の順方向及び質量を有する物体の場合の全方向の速度の加法則は、

　

ｕ1＝ｕ＋ｕ0*(ｃ−ｕ）／ｃ

　

で表す事が可能である事がこれまでに確認されている。

ここで、Ｋ系のｘ座標の係数をｋとして、ｘ座標からＫ'系のｘ'座標に変換する

座標変換式を、

　

ｘ'＝ｘ*ｋ−ｕt　･･･（Ｃ）

ｔ'＝t

　

の形式で表現出来るものと仮定してみる。

ここで、光が慣性系の順方向に向かう場合は、ｘ軸及びｘ'軸の負の方向に向かう

事となるので、（Ｃ）に、ｘ＝−ｃｔ及びｘ'＝−ｃt'及びｔ＝t'を代入すると、

　

ｘ'＝ｘ*ｋ−ｕt

−ｃt'＝−ｃt*ｋ−ｕt

ｃt＝ｃt*ｋ＋ｕt

∴ｋ＝（ｃ−ｕ）／ｃ

　

これを（Ｃ）に代入して、

　

ｘ'＝ｘ（ｃ−ｕ）／ｃ−ｕt　･･･（Ｄ）

　

（Ｄ）を、光の順方向及び質量を有する物質の場合の座標変換式の候補とする。

ここで、慣性系Ｋで速度ｕ0で運動している物体の軌跡(ｘ＝ｕ0ｔ)を慣性系Ｋ'に

座標変換すると、

　

ｘ'＝ｘ（ｃ−ｕ）／ｃ−ｕt

　 ＝ｕ0t（ｃ−ｕ）／ｃ−ｕt

　 ＝−（ｕ−ｕ0*(ｃ−ｕ）／ｃ）t

　

となるが、括弧内は非線形速度の加法則の方程式その物であり、座標変換で必要

となる正しい速度の合成が達成できている事が分かる。

そこで、（Ｄ）を光の順方向及び質量を有する物質の場合の全方向の座標変換式

と暫定的に定める事とする。

　

（慣性系の運動方向（速度ｕの方向）と逆方向に向かう光の場合の座標変換）

順方向の場合に習って、ｘの係数をｋとして、光の逆方向の座標変換式を、

　

ｘ'＝ｘ*ｋ−ｕt　･･･（Ｅ）

ｔ'＝t

　

の形式で表現出来るものと仮定する。

ここで、光が慣性系の逆方向に向かう場合は、ｘ座標及びｘ'座標の正の方向に向

かう事となるので、（Ｅ）に、ｘ＝ｃｔ及びｘ'＝ｃt'及びｔ＝t'を代入すると、

　

ｘ'＝ｘ*ｋ−ｕt

ｃt＝ｃt*ｋ−ｕt

∴ｋ＝（ｃ＋ｕ）／ｃ

　

これを（Ｅ）に代入して、

　

ｘ'＝ｘ（ｃ＋ｕ）／ｃ−ｕt　･･･（Ｆ）

　

（Ｆ）が、慣性系の運動方向（速度ｕの方向）と逆方向に向かう光の場合の座標

変換式となる。

ここで、（Ｆ）のｘの係数である（ｃ＋ｕ）／ｃはローレンツ伸張率βに一致す

る事も納得できる。

　

ところで、最も注意すべき事として、ｘ＝ｕ0ｔ＋ｘ0の様な時間ｔ＝0で原点から

ｘ0変位しているｕ0の速度で運動している物体の場合は、このままを座標変換式

に代入すると、ｘ0にも非線形速度の効果が掛かる結果、正しい変換結果を得る事

が出来無くなる為に、一旦、ｘ軸方向に−ｘ0平行移動した座標を仮に設定して、

座標変換後に元の座標に戻す操作（ｘ軸方向にｘ0平行移動する）が必要となる。

　

（座標の逆変換）

次に、座標変換の逆変換を考察する。

先ず、線形速度の概念の場合（ローレンツ変換やガリレイ変換）の座標変換式の

変形にて逆変換式を求める方法は、非線形速度の場合は利用出来ない。

そこで、ｘ'座標の係数をｋとする座標の逆変換の方程式として、

　

ｘ＝ｘ'ｋ＋ｕt'　･･･（Ｇ）

ｔ＝t'

　

と表現出来るものと仮定してみる。

順方向の光の場合は、光速不変の原理を成立させる為に、ｘ'＝ｃt'及びｘ＝ｃｔ

として、（Ｇ）に代入すると、

　

ｃt'＝ｃt'ｋ＋ｕt'

ｋ＝（ｃ−ｕ）／ｃ

∴ｘ＝ｘ'（ｃ−ｕ）／ｃ＋ｕt'　･･･（Ｈ）

　

（Ｈ）を光を含めた全ての物質の運動まで拡張した座標変換式であると暫定的に

決める事とする。

尚、慣性系の運動方向と逆方向に向かう光の場合（ｘ'＝−ｃt'）は、（Ｈ）から

類推して、

　

ｘ＝ｘ'（ｃ＋ｕ）／ｃ＋ｕt'　･･･（Ｉ）

　

となる。

以上の結果、座標の逆変換の場合は、慣性系の運動方向（ｕの運動方向）の符号

を入れ替える事で達成できる事となる。

　

非線形速度の場合に式を変形する事により対称の式を作ることが出来ない原因は、

非線形速度の順方向と逆方向の効果が異なる為に、変換式を変形した際に非線形

速度の性質の変化（順方向と逆方向）を単一の方程式で一度に表現出来ない事が

原因である。

慣性系の座標変換が一次変換でなければならないという事が必須条件と考えると、

非線形速度の場合は式の変形による逆変換の式が一次式を保つ事が出来ず、座標

及び速度の符号の入れ替えにて逆変換式を作成する事により、慣性系の座標変換

が達成される事となる。

　

これまでの内容を纏めると、一次変換の条件に拘ると、（４）の座標変換式で、

式を代入する際に、非線形速度の順方向と逆方向の性質を考慮して、ローレンツ

収縮率（（ｃ−ｕ）／ｃ）又はローレンツ伸張率（ｃ＋ｕ）／ｃ）を付加する事

が必要であったが、座標と速度の符号を入れ替える事により逆変換を行うという

条件の下で、慣性系の座標変換である（Ｆ）式が成立する事となる。

今回の結果を用いた非線形速度を導入した（４）の座標変換式の改良型の試案を

次に提示する。

　

（５）非線形速度を導入した新しい慣性系の座標変換方式の試案の改良版

　

　　（前提）非線形速度、光速不変の原理、相対性原理

　

　　非線形速度ｕ（＝ｋｃ(１-√(１-(θ/ｃ)^2))）を導入する。

　　但し、ｋを速度の単位ベクトルとして、θ（0≦θ≦ｃ）を線形の変数とする。

　　尚、ローレンツ変換の公式を求める連立一次方程式（線形の変数で構成）を

　　解く手法では、座標変換式の公式を求める事は不可能な為に、非線形速度に

　　は、元々光速不変の原理が織り込み済みであり、又、予め確認している時間

　　と空間の不変性を条件とする事で、連立一次方程式を解く過程を回避する事

　　が可能となる。

　

　　慣性座標系Ｋ（ｘ,ｙ,ｚ,ｔ）に対し,時間t＝0でお互いの系の観測者の原点

　　が一致して速度ｕでｘ軸方向に運動中の慣性座標系Ｋ'（ｘ',ｙ',ｚ',ｔ'）

　　を考えると、座標変換に於いて時間と空間の不変性を保つことが可能となる。

　

　　ｘ'＝ｘ（ｃ−ｕ）／ｃ−ｕｔ

　　ｙ'＝ｙ

　　ｚ'＝ｚ

　　ｔ'＝ｔ

　

　　尚、慣性系の運動方向（Ｘ軸の正の方向では無く、慣性系の速度ｕの方向）

　　と逆方向に向かう光の場合は、上記の座標変換式のｃを−ｃに置き変えて、

　　ｘ'＝ｘ（ｃ＋ｕ）／ｃ−ｕｔ

　　を使用する必要がある。

　

　　更に、ｘ＝ｕ0ｔ＋ｘ0の様な時間ｔ＝0で原点からｘ0変位しているｕ0の速度

　　で運動している物質の場合は、このままを座標変換式に代入すると、ｘ0にも

　　非線形速度の効果が掛かる結果、正しい変換結果を得る事が出来無い為に、

　　一旦、ｘ軸方向に−ｘ0平行移動した座標を設定し、座標変換後に元の座標に

　　戻す操作（ｘ軸方向にｘ0平行移動する）が必要となる。

　

　　尚、逆変換は線形速度の場合の様な式の変形では対処出来ず、各座標の成分

　　及びｕｔの符号の入れ替えのみで行う必要がある。

　

　　＜非線形速度の加法則＞

　　ｕ1＝ｕ＋ｕ0*(ｃ−ｕ）／ｃ

　

　　但し、逆方向の光（ｕ＝−ｃ又はｕ0＝−ｃ）の場合は、ｃを−ｃに置き換え

　　て、

　　ｕ1＝ｕ＋ｕ0*（ｃ＋ｕ）／ｃ

　　を使用する必要がある。

　

今回の非線形速度の概念を導入した座標変換式を求める際に、現行の数学理論の

守備範囲から外れた非線形数を物理学の理論に矛盾無く取り込む為に、暗中模索

で試行錯誤した経験を踏まえて、少し総括的な感想を述べたい。

ローレンツ変換の公式を求める連立一次方程式は、線形代数学という線形変数を

対象とした数学理論体系であり、この手法をそのまま踏襲して非線形速度を含め

た連立一次方程式の解を求めても、結果的には線形の変数である速度としての解

が求まるだけであり、非線形速度を含めた解を求める事は論理的に不可能という

事になる。

そこで、非線形数までも取り扱いが可能な数の範囲を拡大した「非線形代数学」

なる新しい数学体系の創設を願うものである。

また、現行の手法では、非線形速度は線形速度を使って間接的にしか表現が出来

ない数学の環境にあり、三角関数や指数関数の様に、非線形速度を独自な関数で

ダイレクトに表現できる環境が必要と考える。

　

特殊相対性理論の線形速度の概念の基に於いては、慣性系の速度ｖ１と慣性系に

静止している物体の速度ｖ２とは当然ながら一致する（ｖ１＝ｖ２）という極当

たり前の理解がこれまでに疑問の余地の無い常識として信じられてきているが、

慣性系に静止している物体はローレンツ収縮や時間の遅れや同時刻の相対性とい

う光速不変性を成立させる為の相対論的効果が及ぶ事を考慮すると、果たして、

ｖ１＝ｖ２が成立するのかという疑問を持つべきである。

非線形速度の概念を手に入れた現在、線形速度の概念の基の特殊相対性理論とは、

座標変換の際に元来在るべき非線形速度の性質を表現する為に、線形速度として

の慣性系の速度ｖ１とこの慣性系に静止している物体の真の速度ｖ２との関係に

於いて、ローレンツ収縮と時間の遅れ、更には時刻の相対性という本来は不変で

あるべき基本的な３つの物理量を線形速度ｖ１をパラメータとして代償的に変化

させる事により、慣性系に静止した物体の真の速度ｖ２が実質的に非線形速度の

変化を行う事となり、辛うじて数学上辻褄が合う様に光速不変の原理を満足する

為の座標変換の公式を定式化する事が出来たものであると解釈する事が出来る。

つまり、観測の対象となる任意の物体の速度は非線形速度の性質を持ったｖ２を

指し、慣性系の速度ｖ１は観測の対象とはならない架空の線形速度という事にな

り、つまりｖ１≧ｖ２の関係にあり、ｖ１を線形速度ｖ、ｖ２を非線形速度ｕに

置き換えたものが、これ迄に漠然と記述してきた非線形速度と線形速度の関係式

である、

　

ｕ＝ｃ(１−√(１-(ｖ／ｃ)^2))

　

であるが、本質的には慣性系の速度という概念に於ける実際に観測可能な非線形

速度ｕと観測不能な架空の線形速度ｖの関係式であると解釈する事が正確な理解

である。

勿論、非線形速度の概念に於いては、座標変換に於ける相対論的効果など無く、

速度以外の基本的な物理量は不変であり、慣性系の速度と慣性系に静止した物体

の速度とが厳密に一致する事は言うまでも無い。

　

D節＞非線形速度の概念の基での新しい力学概念

質量とは、慣性質量（物質の動き難さの指標）と重力質量（物質間に働く重力の

強さの指標）の２種類があり、これまでの精密な実験の結果として、この２種類

の質量はほぼ等しい（異なる可能性は極めて少ない）事が証明されている。

ここで、物質の持つ全エネルギーは、一般的に質量エネルギーと運動エネルギー

の合計で表されるが、現行の相対論では質量としての静止質量ｍ0を不変と考えて

いるので、速度ｖに依存した運動エネルギーの増減分に依り物質の全エネルギー

が増減する。

　

ニュートン力学を更に自然の本質的な法則に集約する目的で解析力学が構築され、

量子力学の基本方程式であるシュレーディンガー方程式の基礎方程式に採用され

ているハミルトニアンとして、その真価が発揮されている。

物質の全エネルギーを表すハミルトニアン（Ｈ）の形式は、

　

Ｈ＝（全エネルギー）＝（ポテンシャル・エネルギー）＋（運動エネルギー）

　

そこで、静止質量ｍ0の自由粒子の相対論的ハミルトニアンは、

　

ｍc^2＝ｍ0c^2/√(１-(v/c)^2)

＝ｍ0c^2+ｍ0c^2{１/√(１-(v/c)^2)-1}

＝ｍ0c^2+ｍ0c^2{（1-√(１-(v/c)^2)/√(１-(v/c)^2)}

＝ｍ0c^2+ｍ0c^2{(1-√(１-(v/c)^2)*(1+√(１-(v/c)^2)/√(１-(v/c)^2)*

（1+√(１-(v/c)^2))}

＝ｍ0c^2+ｍ0c^2{v^2/c^2/√(１-(v/c)^2)*(1+√(１-(v/c)^2))}

＝ｍ0c^2+ｍ0v^2/{√(１-(v/c)^2)*(1+√(１-(v/c)^2))}

　

∴ ｍc^2

＝ｍ0c^2/√(１-(v/c)^2)

＝ｍ0c^2＋ｍ0v^2/{√(１-(v/c)^2)*(1+√(１-(v/c)^2))}　・・・（Ａ）

　

ここで、ｖ⇒ｃの極限では、式（Ａ）はエネルギーが無限大に発散する事となり、

光の１つのモデルである光子の質量をゼロとする必要が生じる。

そこで、光は質量がゼロという事で、質量が無ければ、最早、光に慣性の法則は

適用出来ない（光は慣性運動しない）とか、重力場で光が曲げられる（光に重力

が作用する）筈が無いとか、極めつけとして、光は物質では無いとか言う素朴な

疑問が湧く事も無理からぬ事である。

又、ｖ⇒ｃの極限での式（Ａ）の静止質量ｍ0をゼロとすれば、エネルギーの発散

を防ぐ事は出来るが、式（Ａ）の左辺及び右辺の第二項が0/0という不定値となり、

光のエネルギーを正しく導く事は出来ない。

それでは、光（光子）のエネルギーはどの様にして求められているかという事に

なるが、光の質量をゼロとすると、ニュートン力学の運動量ｐ＝ｍ0ｖからは光の

運動量ｐ＝0となり矛盾する事となるので、振動数νの光子のエネルギーＥ＝ｈν

で表される事を利用する事により、光子の運動量ｐ＝ｈν／ｃとなる。

そこで、質量を有する物質から質量ゼロの光までカバーする自由粒子の運動時の

全エネルギーを表す式は、下記の方程式となる。

　

Ｅ＝√（（ｍ0ｃ^2）^2＋（ｐｃ）^2）・・・（Ｂ）

　

但し、質量を有する物質（ｍ0≠0）の場合は、ｐ＝ｍ0ｖ／√(１−(ｖ／ｃ)^2)、

光（ｍ0＝0）の場合は、ｐ＝ｈν／ｃを充てる事が必要である。

尚、式（Ｂ）は、当然ながら、自由粒子の相対論的ハミルトニアンの式（Ａ）と

同値である。

　

　ここで元に戻って、自由粒子の相対論的ハミルトニアンの式（Ａ）は、ｖ⇒ｃ

の極限ではエネルギーが無限大に発散する事となり、光の質量がゼロである事が

必要であるという事であったが、この本質的な原因は、座標変換に依り自由粒子

の全エネルギーが増減する事であると結論する事が出来る。

又、全エネルギーが増減する原因を質量が増減する事（相対論的質量ｍ）に求め

ると、重力質量と慣性質量の等価性に依り、運動物体に及ぶ重力が相対論的質量

に依存して変化する事で矛盾が生じる事となり、物質が有する質量とは静止質量

ｍ0（不変）を指すという事で矛盾が生じない様に配慮されている。

それでは、座標変換に依存して増減する運動エネルギーは物理的に何を意味して

いるのかというもっと根本的な疑問が生じる事となる。

エネルギーＥ（つまり、光のエネルギー）と質量ｍ（物質の質量）が等価という

認識（Ｅ＝ｍｃ^2）からは、残るは光のエネルギーという事になる。

つまり、座標変換に依り光が生じて自由粒子が光の衣を纏うという解釈になる。

しかし、光が重力場で曲がる現象（重力場レンズ効果）から、質量がゼロの光の

エネルギーが重力場の影響を受けるという事実から、自由粒子が光の衣を纏って

いるという解釈に於いても、光の衣の分のエネルギーが重力場での影響を増加さ

せる作用を生じるという矛盾する結果をもたらす事には変わらない。

つまり、座標変換に於ける自由粒子のエネルギーの増減は、実体の無い見かけの

エネルギーの増減と解釈する以外に矛盾を回避する事が出来ないという事になる。

そこで、あくまで実体の無い見かけのエネルギーの存在を仮定し通すか、大元の

自由粒子の相対論的ハミルトニアンの式（Ａ）を見直すかという選択に迫られる

事になる。

後者を選択すれば、自由粒子の持つ全エネルギーは、時間発展並びに座標変換に

於いて不変と仮定しなければならない事となる。

　

ここで、素量子の運動状態式を基礎とする物質（素量子の集合体）の運動状態式

を再掲する。

　

ｍ0c^2

＝ｍ0c^2√(１-(v/c)^2)+ｍ0c^2(１-√(１-(v/c)^2))

＝ｍ0c^2√(１-(v/c)^2)+ｍ0c^2（１-√(１-(v/c)^2))*（1+√(１-(v/c)^2)/(1+

√(１-(v/c)^2))

＝ｍ0c^2√(１-(v/c)^2)+ｍ0c^2(v^2/c^2/（1+√(１-(v/c)^2))

＝ｍ0c^2√(１-(v/c)^2)+ｍ0v^2/（1+√(１-(v/c)^2))

　

∴　ｍ0c^2＝ｍ0c^2√(１-(v/c)^2)＋ｍ0v^2/（1+√(１-(v/c)^2)) ・・・(Ｃ）

　

ハミルトニアンの形式と比較すると、左辺は物質の全エネルギーを表し、右辺の

第一項は質量エネルギーであるが、ポテンシャル・エネルギーに相当する不顕性

エネルギーを表し、第二項は運動エネルギーという顕性エネルギーを表す事とな

り、素量子の集合体である質量を有するすべての物質の運動状態式は、奇しくも

ハミルトニアンと一致する事が解る。

そこで、式（Ａ）の自由粒子の相対論的ハミルトニアンに対して、式（Ｃ）を、

自由粒子の素光子説的ハミルトニアンという名称で呼ぶ事とする。

式（Ａ）と式（Ｃ）のそれぞれの右辺の第二項は運動エネルギーを表しているが、

ｖ<<ｃで何れもｍ0v^2/2となり、ニュートン力学に於ける運動エネルギーに一致

する。

ここで、式（Ｃ）の両辺にローレンツ因子γ（１／√(１−(ｖ／ｃ)^2)）を掛け

ると、式（Ａ）と同じ式となる。

つまり、自由粒子の相対論的ハミルトニアンと素光子説的ハミルトニアンとは、

本質的には等価の式という事になる！。

違いとしては、相対論では静止質量エネルギーｍ0c^2（一定）に速度に依存する

運動エネルギーが加わる事により自由粒子の全エネルギーがγの割合で増減する

事となり座標変換に於いてはエネルギー保存則が成立しないが,一方,素光子説的

ハミルトニアンでは、自由粒子の全エネルギーは速度に依存して質量エネルギー

と運動エネルギーが相補的に変化する事により速度に関係なく一定であり、その

結果、時間発展に限らず座標変換に於いて自由粒子の全エネルギーは不変となり、

エネルギー保存則が完璧に成立する事になる。

これは、偶然の結果では無く、約１世紀の長き間に培われてきた相対論的力学の

正当性を背景として、自然の真理のベールが更に１枚剥がれた事を意味するもの

と考える。

式（Ｃ）でｖ⇒ｃの極限では、右辺の第一項の質量エネルギーの項がゼロになり、

第二項の運動エネルギーの項がｍ0c^2となり、光速ｃで運動している物質である

光のエネルギーがｍ0c^2という解釈が出来る事となり、光の質量に相当するｍ0を

ゼロとする必要は無く、光もエネルギーに相当する質量を持つ事とすれば、多く

の素朴な疑問が解消される事となる。

式（Ｃ）に於いて物質の最高の速度ｃでは、質量エネルギーがゼロつまり、全て

のエネルギーが運動エネルギーだけになり、運動エネルギーを物質の運動に直接

寄与している顕性エネルギーと考えて、質量エネルギーを物質の運動に寄与して

いない不顕性エネルギーと解釈すれば、不顕性エネルギー（質量エネルギー）が

ゼロという、即ちフル・パワーで顕性エネルギー（運動エネルギー）を最大限に

発揮して運動しているからこそ、光が物質の取り得る最高速度ｃで常に運動して

いるという解釈が出来る。

以上の考察から、現行の理論に於ける光の質量をゼロと解釈する代わりに、質量

エネルギーをゼロとして、更に質量の概念を変更して、光又は物質を構成してい

る素光子又は素量子の個数という解釈が最も相応しいと考える。

　

不顕性エネルギーをポテンシャル・エネルギーと等価と考えると、自然の本質的

な法則を求めて到達したハミルトニアンが、質量を有する全ての物質が素量子の

集合体であるとする素量子の基本的な運動状態式と一致する事は偶然では無く、

むしろ自然の本質の的を射た必然的な結果と考える。

又、全ての物質が素量子の集合体と仮定し素量子の固有質量の不変性を課すと、

一定のエネルギーでの物質の加速効果が、光速に近づくに連れて低下する現象

（物質の運動の頭打ち現象）が生じることで、非線形速度の存在を推定する事が

出来た訳であるが、現行の素粒子としての電子やニュートリノや、クウォークの

複合粒子としての陽子や中性子や各種の中間子の概念ではこの様な非線形速度を

生じる原因をそれぞれの粒子自身の性質に求める事は出来ない。

　

素光子説的ハミルトニアンの両辺にローレンツ因子γ（１／√(１-(ｖ／ｃ)^2)）

が掛かったのが相対論的ハミルトニアンという事になるが、この本質的な事柄は、

特殊相対性理論の前提である暗黙の線形速度の条件の基で、実際の自然現象とし

ての非線形速度の性質（主に、物質の運動の頭打ち現象）を無意識の内に実現す

る為に、ローレンツ因子の付加が必要になっていると解釈する事が出来る。

更に付け加えると、相対論的ハミルトニアン（Ａ）は、素量子の集合体としての

物質（例えば、電子）を加速器で加速した場合の加速の為に与えられた電磁場の

エネルギー分が物質の運動エネルギーの増加分として物質の全エネルギーが増加

した場合に相当するが、相対論では、このエネルギーの増加が座標変換でも生じ

ていると解釈している事が本質的な間違いであると考える。

但し、線形速度の概念の基で物質の運動の頭打ち現象を説明する為には、止む無

く相対論的質量（光速に近づくに連れて質量が無限大に発散する為に光速に達す

ることは不可能）という概念を導入しなければならない事も理解できる。

　ここで、非線形速度の概念を導入すれば、相対論的質量の概念は不要となり、

相対論的ハミルトニアン（Ａ）の両辺のローレンツ因子γを取り除くことにより、

この式が素量子の運動状態式を基本方程式として素量子の集合体である自由粒子

の素光子説的ハミルトニアン（Ｃ）に帰着する事となる。

何れにしても、自由粒子の素光子説的ハミルトニアンと相対論的ハミルトニアン

の２つの方程式が、素光子説的力学と相対論的力学の本質的な違いを端的に表し

ている事となり、素光子説的ハミルトニアンが相対論的ハミルトニアンに代わる

新しい力学理論の基本方程式として十分に通用する目処が付いたものと考える。

　

巨視的に考えると、物質の構成要素である素量子の運動状態に於けるエネルギー

の割合を示す方程式が、自然の本質を探究するニュートン力学を発展させた結果、

構築された解析力学の集大成である時間発展に於けるエネルギー保存則を前提と

するハミルトニアンの形式と一致する事は、至極当然の事と思われる。

ハミルトンの変分原理（作用積分（ラグランジアンの時間積分）が最小値を取る

様に全ての物質の運動が規定されている）という経験則も、素光子の作用が最小

となる運動を行う基本的な性質（フェルマーの定理）を有していると解釈すべき

であり、素量子を構成要素とする全ての質量を有する物質が、最小作用の法則を

満足する運動を行う事も、素量子（素光子）の基本的な性質の表れと理解すべき

であろう。

この結果、素量子の運動状態式が万物の振る舞いを説明する基本方程式であり、

この方程式からニュートン力学の力や加速度の定義やそれらを組み合わせた多く

の自然法則が導き出せる見通しがついたものと考える。（巻末の参考文献Ｉ）

なお、全ての物質の運動がニュートン力学のＦ＝ｍαという簡単な運動方程式で

表現出来る事（経験則）は大変驚くべき事実であるが、全ての物質が素光子又は

その束縛状態である素量子の集合体と考えれば至極当然の事である。

　

ここで、非線形速度の性質を表す方程式ｕ＝ｃ(１−√(１−(ｖ／ｃ)^2))に於い

て、現行の力学の慣習に従い、加速度を考えてみる。

　

非線形速度ｕの加速度（ｄｕ／ｄｔと表記）を現行の線形代数学上の微分の手法

を用いて直接に表現する事は不可能（結果は不定となり、微分の値が一意的には

決まらない）であるが、現行の線形速度ｖとの関係式を用いると、

　

ｄｕ／ｄｔ

＝ｄ（ｃ(１−√(１−(ｖ／ｃ)^2))）／ｄｔ

＝（ｖ／√(ｃ^2−ｖ^2)）ｄｖ／ｄｔ

＝ａ*tanθ

　

加速度の次元を持つａは、現行の線形速度の概念上でのニュートン力学に於ける

加速度（α=ｄｖ／ｄｔ）と同等であろう。

また、θは直角三角形の斜辺をｃ、高さをｖ、底辺を√(c^2−v^2)とした場合の

斜辺と底辺に挟まれた角度であるが、ｖ⇒ｃでtanθ⇒∞となり、光速ｃに近付く

為には、加速する為に与えるエネルギーを無限に増加させる必要があるという、

相対論の解釈と同等の「物質の運動の頭打ち現象」を表している式と解釈できる。

以上の様に、非線形速度を、元来では線形の物理量にしか適用出来ない微積分の

方程式としてダイレクトに表現する事は出来ないが、その非線形の物理量の性質

を忠実に表現できる線形の物理量だけで構成されている方程式が存在していれば、

この非線形の物理量その物をその方程式で置き換える事により、非線形の物理量

を含んだ方程式に於いても微積分の演算が適用可能となると考える。

以上の結果、非線形の物理量としての速度は、線形の変数を用いた関数で完全に

表現できる事となり、現行の線形代数学の範疇で取り扱うことが出来る物理量で

ある事が証明できたものと判断する。

更に、非線形速度が線形の数を介する関数で間接的に表現しなければならいとい

う事は、速度という物理量が温度という物理量と同様に自然現象の基本的な要素

を表現する物理量では無いという事を示唆しているものと考える。

素量子の運動状態式は、運動状態の程度を表す指標として運動エネルギーで表現

しているが、これは、現行の力学に於けるハミルトニアン形式と同一の思想であ

り、物質の運動状態を評価する指標としては、速度よりも運動エネルギーがより

重要である事の証左であると言えるが、質量という基本的な要素の物理量が付加

されている事から考えても、より基本的な物理量では無い事は確実であろう。

速度や運動エネルギーの様な運動状態の程度を表す物理量は、隠れた最も基本的

な物理量の二次的な指標であると考えねばならない。

速度や運動エネルギーが非線形に変化する事も、これらが二次的、更には三次的

な物理量である事が示唆される。

運動エネルギーは速度よりも確かに物質の運動状態に関する情報を多く内存して

いる更に重要な物理量であるが、これは質量という物理量と速度という物理量

の複合的な物理量と考えれば当然の事であるが、より基本的な物理量という訳で

は無いという事である。

もし、更に基本的な物理量が存在するとすれば、素光子その物の基本的な性質を

解明する事が必要であり、その候補としては、不変量としての素光子及び素量子

の固有エネルギーεという事になる。

余談ではあるが、量子力学に於ける量子の不確定性に反対したアインシュタイン

らは、局所性の隠れた変数理論を提出して否定される結果となったが、未だ発見

されていない物質の基本的な性質を規定する変数（物理量）が存在する可能性を

検討する価値が大いにあると考える。

　

素光子説では、質量とは、物質を構成する素量子の個数程度の意味で使用する事

が適当と考えている。

運動エネルギーは、物質の持つ全エネルギー（一定値）に運動エネルギーの変化

の割合を表す係数；１−√(１−(ｖ／ｃ)^2)を掛けた値として表現されているが、

速度は、最大の速度である光速ｃ（一定値）にこの係数を掛けたものとして表現

されている事を考えると、この係数こそ、運動エネルギーと速度の双方の共通の

基本的な物理量と考える事も可能という事で、この係数を運動発現率と呼ぶ事と

すれば、無次元数という事も考慮すると、自然の持つ基本的な非線形速度の性質

を表しているという解釈が出来るかも知れない。

これは、微細構造定数の様な無次元の基本的な定数（静止画の例え）に対比され

るべき基本的な無次元の変数（動画の例え）と解釈すべきかも知れない。

非線形速度の性質を、任意の慣性系の時間を不変に保つ事を前提にして決定して

いるが、本来は物質を構成している素量子の集団の振る舞いを定式化する事から

論理的に導き出さなければならないと考える。

その為には、エネルギー保存則を基本原理として、物質を構成している素量子の

個数と加速の為に与えられたエネルギーとしての素光子の個数の関係式から出発

する事は当然であるが、物理理論に必須の速度の概念をどの様なアプローチにて

導入する事が適当であるかを考察して実現しなければならないという課題が残っ

ている。

尚、余談であるが、円周率πや自然対数の底ｅは線形の数で表現できない無理数

であるが、線形の変数で表現できない非線形の物理量（例えば、距離？）が存在

する場合は、この非線形の物理量に関する演算を実現する為にはどの様な解決法

があるかという疑問が残る。

その根本的な解決策として、非線形代数学と仮称したい新しい数学分野の構築が

必要となるかも知れない。

　

　この節でのこれ迄の考察から明らかになった事柄の本質を一言で言えば、古来

から当然と信じられてきた速度の線形性の概念を前提にした特殊相対性理論では、

光の速度に限らず、光の振る舞いが任意の慣性系で同じになる様に設定する事は

全く不可能であったが、非線形速度の概念を導入すればこれが可能となり、座標

変換に於ける時間や空間、更には質量の不変性というニュートン力学の自然観に

回帰する事が出来る様になるという事である。

勿論、同時刻の相対性という奇妙なパッチ処理も必要が無くなる事となる。

更には、素量子の運動状態式を基に、新しい力学の再構築が必要である。

その結果、例えば、ハミルトニアンを利用した量子力学での物質の波動性を表す

基本方程式であるシュレーディンガー方程式と素量子の運動状態式を比較検討す

る事により、量子力学の新しい側面が見出されてくる事が予想される。

　

物理現象とは、素光子や素量子の集合体である物質や物質間の相互作用に於ける

エネルギー（全てが素光子や素量子の運動エネルギー）の交換がその主体である

と考えるが、運動エネルギーの交換の指標を、より身近に感じる力という概念に

置き換えて表現する理論が力学であるという事が出来る。

また、物質について考えると、素光子が束縛状態にある素量子の集合体を不顕性

エネルギーを持った物質として感じ、物質の不顕性エネルギーの一部が顕性化し

ている状態（顕性エネルギーとしての運動エネルギーが発現した状態）が物質が

運動している状態であり、その状態をより直接的に感じ取る指標に置き換えを行

っている訳であるが、その指標が速度という事になる。

　

素量子の運動状態式を基本式として新しい座標変換式を考えた場合に、慣用的な

相対性原理という公理を前提にする代わりに、素量子の運動状態式が座標変換に

於いて不変である事を前提として理論を構築し、その解を総称して相対性法則

（あるいは絶対性法則）とする筋書きが妥当ではないかと考える。

　

ここで、このレポートの文末の素量子の運動状態式の時間発展に於ける推移を表

している概念図のシンボル記号を利用して、素光子や素量子の固有エネルギーを

○＝ｈ／ｓで表し、素量子（素光子）の固有質量を●＝○/c^2で表す事とする。

電子の持つ全エネルギーＥは、ド・ブロイ波の性質から、Ｅ＝ｈνで与えられる。

つまり、電子はν（整数に変更し、無名数と見なす）個の素量子から構成されて

いる事になり、電子の運動状態式は、

　

Ｅ＝ｈν＝○ν＝●ｃ^2ν

　＝●ｃ^2ν√(１−(ｖ／ｃ)^2)＋○ν(１−√(１-(ｖ／ｃ)^2))　　･･･（Ｄ）

　

この右辺の第二項の(１−√(１-(ｖ／ｃ)^2))が運動エネルギーの発現率を表して

いると解釈出来る。

運動エネルギーの発現率をｋ（ｖ）＝１−√(１-(ｖ／ｃ)^2)とすれば、

　

（第二項の運動エネルギー）

＝○ν(１−√(１-(ｖ／ｃ)^2))

＝ｋ（ｖ）○ν

　

ここで、非線形速度ｕ＝ｃ(１−√(１-(ｖ／ｃ)^2))を別の角度から眺めると、

最高速度ｃに速度の発現率ｋ（ｖ）を掛けたものであり、ｕ＝ｃｋ（ｖ）となる。

これは、任意の慣性系に於ける光の振る舞いが静止時と同じという条件で設定し

た非線形速度の性質に従って運動エネルギーの発現率が変化するという事は、単

なる偶然の一致では無く、自然の根源的な摂理に関わる最も重要な事柄と解釈す

れば、この事柄は素量子の運動状態式の妥当性を更に支持する結果と考える。

又、運動エネルギーの発現率という新しい物理量が根源にあり、物質の相対的な

運動速度ｕは、何と！、二次的な物理量という解釈になる。

この解釈は、現行の解析力学で位置と正準共役である運動量を、物質の運動状態

の程度を表す指標として、速度より更に本質的な物理量であるとする現行の解釈

を更に進めて、運動エネルギーこそ物質の最も基本的な運動状態を表す指標であ

ると言う事になるが、解析力学のハミルトニアンが運動物体の持つ全エネルギー

を表す方程式であり、量子力学に応用されている事からも納得される事であろう。

素量子の速度は、最大の速度としての非束縛状態である素光子の定常の運動状態

である速度ｃに運動エネルギーの発現率を乗じたものであり、素量子の集合体で

ある質量を有するすべての物質の運動速度という事になる。

尤も、実際に物質の運動状態を観測する場合に、先ず最初に測定可能な物理量は、

単位時間に移動する距離で定義されている極めて実践的である現行の速度であり、

運動エネルギーは物質の質量が測定されて初めて導出できる物理量である事を考

えると、意外な感じが生じることは無理からぬ事ではある。

また、物質のエネルギーや質量は、物質を構成している基本粒子である素光子や

その束縛状態である素量子の固有エネルギー（不変量）や固有質量（不変量）の

整数倍という関係から、それらは基本粒子の個数という事が本質的な意味合いと

なると考える。

今回、素量子の運動状態式の重要な解の一つである「物質の運動の頭打ち現象」

を現行の理論に適用する手段としての非線形速度の概念を導入して、ローレンツ

変換に代わる時間と空間を不変とする新しい慣性系の座標変換方式が成立する事

を証明する事が出来た事は、素量子を構成要素とする全ての質量を有する物質と

素光子を構成要素とする光との間の相互作用に関し、任意の慣性系で時間と空間

を不変として全く等しく成立する事を証明した事を意味し、素光子説の妥当性を

更に強く示唆する事柄と考える。

　

（Ｄ）で、線形速度ｖに対応する、非線形速度ｕ＝ｃ(１−√(１-(ｖ／ｃ)^2))を

代入すると、

　

電子の運動状態式；ｈν＝●ｃ^2ν＝●ｃ^2ν（ｃ−ｕ）／ｃ＋○ν･ｕ／ｃ

　

右辺の第一項が電子の不顕性エネルギー（ポテンシャル・エネルギーに相当）を

表し、第二項が電子の顕性エネルギーである運動エネルギーを表している。

なお、座標変換に於いて、物質の運動状態式の全エネルギーは不変であるので、

この場合の電子の振動数νは不変数（座標変換で不変）と置かなければならない。

　

ここで、この節でのこれ迄の考察の流れを纏める事とする。

線形速度を前提とする特殊相対性理論の時間の遅れは、慣性系の運動方向だけに

向かう光と物質との関わり合いという設定の基で導出された一つの解であるが、

ローレンツ収縮という物質及び空間の収縮の存在も予想しており、光が慣性系の

運動方向に向かう際に空間の伸張を感じ、更に空間の収縮であるローレンツ収縮

が加味される事となるが、ここで、空間の伸張率がローレンツ収縮率の逆数とな

る様な非線形速度を設定すれば、空間の伸張効果と空間の収縮効果が打ち消し合

って、光は静止時と同じ空間状態を感じる事となり、結局、光の物質との関わり

合いに於ける所要時間は静止時と等しくなる。

一方、慣性系の運動方向と逆の方向に向かう光は、空間の収縮効果を感じるが、

順方向で設定した非線形速度をそのまま使った場合は、その逆方向の性質である

ローレンツ伸張効果にて両方の効果が打ち消し合う結果、光は静止時と同じ空間

状態を感じる事となり、結局光の物質との関わり合いに於ける所要時間は静止時

と等しくなる。

つまり、任意の慣性系に於ける光と物質の関わり合いに於ける光の所要時間は、

静止時と変わらず不変である事になる。

又、この非線形速度を物質と物質との関わり合いで使用した場合に、慣性系に於

ける任意の物質の運動の場合の所要時間は静止時と変わりなく不変である事が分

かった。

　

以上の結果、任意の慣性系の物理法則は同じ形式で表現できるが、相対速度に応

じて時間や空間や質量が相対的に変化すると解釈している特殊相対性原理に対し、

非線形速度の概念を導入すれば時間に関して不変であり、更にローレンツ収縮は

非線形速度の順方向の性質がもたらす数学上の架空の現象である事が解り、物理

現象は静止時と変わりなく同等であるという更に厳密な同等性を保証する新たな

相対性原理を仮定する事が可能という結果を得た事となる。

　

Ｃ節からＤ節迄の流れを纏めると、質量を有する全ての物質を素光子の束縛状態

である素量子の集合体と仮定して、素量子の固有エネルギーを不変と仮定すると、

座標変換に於いても質量を有する物質の全エネルギーが保存される事となり、更

に、光のエネルギーも座標変換に於いてエネルギーが保存される事と併せると、

エネルギー保存則が自然の法則の中で基も基本的な法則（摂理）と位置付ける事

が出来ると考える。

　

運動量について一言言及すると、ニュートン力学に於ける運動量の定義ｐ＝ｍｖ

からは、特殊相対性理論は勿論、非線形の速度の概念上でも運動量保存則は成立

しないが、特殊相対性理論的力学の運動量の定義上では時間発展で運度量保存則

が成立する（様に作られている）が、座標変換ではこれが成立しない事を考える

と、エネルギー保存則は運動量保存則より普遍的な法則である事が分かる。

この根本的な違いは、エネルギー保存則は、エネルギーと質量の等価式E=mc^2を

取り込む事により全エネルギー（質量エネルギー＋運動エネルギー）が座標変換

に於いても不変となる事を可能とした事でる。

つまり、運動量には、エネルギーと質量の等価式に対応する様な等価式は無い。

　

なお、素量子の運動状態式で運動エネルギーの発現率の項に光速ｃを付加すると、

非線形速度の次元を持つが、この速度の性質が「物質の運動の頭打ち現象」を生

じる物質の運動状態と等価という事を推定し、現行の線形速度をこの非線形速度

で置き換えてやると、何と光速不変の条件下での慣性系での座標変換で、時間と

空間を不変に保つ新しい座標変換が可能となる事が証明される事になり、現行の

相対性原理を更に普遍な原理に昇格させる事が可能となったものと考える。

　

　特殊相対性理論の解（ローレンツ収縮、時間の遅れ）を新しい自然現象の発見

と解釈する事は誤った判断であり、物質の速度が光速に近づくに連れて、物質の

加速効果が鈍化する現象（物質の運動の頭打ち現象）の存在の必要性を論理的に

要請したものであり、この真の現象を新しく前提に加える事により相対論的効果

という数学上の架空の現象が論理的に生じる必要性が無くなるものと考える。

また、空間の対称性に依り、同時刻の相対性というパッチ処理も不要となる。

ここで一つ注意したい事柄としては、時計の遅れという物理現象に関して、時間

の遅れと物質の運動の鈍化という２通りの解釈が可能であるが、元来、時間とは

事象の移り変わりの割合を客観的に定量的に計る一種の物差しとして定義された

ものであり、時計の遅れを生じさせる現象が見つからない場合に限り、応急的に

時計の遅れを時間の遅れと解釈することは許されても、実際に物質の運動の鈍化

という現象が明らかになれば、当然ながら時間の遅れという解釈は速やかに破棄

されるべきものと考える。

ところで、重力場中や加速運動中で観測される時計の遅れは、慣性運動中の物質

の運動の鈍化という観測者の系に依存して生じる相対的ないわば見かけの現象と

は対照的に、重力という力学的な原因で時計の時刻を刻むメカニズムを司る物質

の運動が鈍化する事により生じる絶対的な現象であり、これを時間の遅れと判断

する事は誤りと考える。

この様に、特殊及び一般の相対性理論に於ける時間の遅れの解釈は間違っている

事になると考える。

　

　ここで、「物質の運動の頭打ち現象」を別の観点で考えると、古来より当然で

自明の事柄と信じられてきた速度の線形の概念を破棄し、非線形の物理量に変更

する是非を検討すべき時期に来ているものと考える。

「物質の運動の頭打ち現象」とは、元々、全ての物質を素量子の集合体と仮定し

た場合の、素量子の固有エネルギーが不変である事を前提として導かれた物質の

運動状態で現れる性質であり、我々が日常的に経験する何らかの外力や質量増加

等の要因にて物質の運動にブレーキが掛かった状態ではなく、素量子の集合体の

振る舞いを速度という非線形の物理量の特性に置き換える事により、物質の運動

状態が忠実に表現されているに過ぎない（即ち、慣性の法則を満足する）という

解釈が妥当であろう。

　

　力学理論の発展の歴史を顧みると、ニュートン力学は、速度が線形に変化して

無限大まで可能とする至極当たり前と思われる速度の概念を前提のガリレイ変換

の基で、空間の一様性や時間の普遍性を基本的な自然観とする素朴な理論であり、

日常経験する比較的低速の慣性系では、何ら不都合を生じる事は無く、自然現象

を良く記述できていた。

つまり、光速の無限大性と速度の線形の概念は、何れも間違った概念ではあるが、

これらの組み合わせはそれなりにうまくマッチングして、空間と時間の不変性が

幸運にも保たれていた訳である。

一方、特殊相対性理論は、光速に関して有限性と不変性という修正を加えること

により、ニュートン力学より一歩前進した力学理論であるが、光速不変の原理と

共に自然の秩序を保つ為に必要なペアの片方である「物質の運動の頭打ち現象」

という物質固有の基本的な性質を欠いたままで構築された理論であり、相対論的

効果という時空間の多様性の可能性を提示し、物理学の自然に対する視野を拡大

させた功績は評価出来るが、任意の慣性系に於ける光の空間及び時間的な非対称

性を取り繕う為に、同時刻の相対性という人為的な万能のパッチを当てる必要も

有った訳である。

つまり、光の速度の有限性及び不変性と線形速度との組み合わせは、正しい概念

と間違った概念の組み合わせであるために、当然ながらミスマッチングとなり、

その結果、矛盾が生じない様に論理展開を行う上で、相対論的効果という不思議

な現象を想定せざるを得なくなった訳であり、物質の速度が線形に増加して最大

速度ｃで突然途絶する事は大変不自然な現象と言わざるを得ず、現行の線形速度

の概念を「物質の運動の頭打ち現象」即ち物質の運動の鈍化と等価と考える速度

を非線形の概念に変更する事により、光速ｃを速度の上限とする物質の運動速度

の有限性と速度の非線形の概念の組み合わせが自然現象として調和のとれたもの

となり、相対論的効果という不思議な自然現象の必要性を論理的に要請する必要

も無くなる事となる。

つまり、速度の有限性と非線形の概念はニュートン力学に於ける速度の無限大性

と線形の概念と自然現象的には大変類似した概念と考える事が出来る事となり、

速度の非線形の性質に於ける極限値としての最大速度ｃは、速度の線形の性質に

於ける無限大の速度に対比出来る事となり、光速不変性もこの性質の現れと捉え

る事が出来る。

　

光速不変の原理が発見される以前の物質の運動速度に上限がないであろうとする

素朴な古来からの考えの基での速度が線形の性質を持つ物理量であると考える事

は極自然な判断であるが、光速不変の原理の発見を契機として速度の概念の見直

しという当然と思える作業が今日まで行われて来なかった原因は、古来から自明

と考えられてきた速度の線形性をわざわざ物理理論の前提（仮定）とするまでも

無いとの共通した潜在的な認識があった為であろうと考える。

　

ここで、速度の加法則という公式の側面から、速度の性質に関して考えてみる。

時間と空間を不変とするガリレイ変換では、速度ｖ1、ｖ2が線形であり、

　

ｖ＝ｖ１＋ｖ2

　

となり、文字通り、速度ｖは線形（足し算可）で無限大まで許容される事となる。

一方、光速不変の原理を新しく導入し、速度の上限が光速ｃとなったローレンツ

変換では、速度ｖ1、ｖ2は依然として線形であるが、

　

ｖ＝（ｖ１＋ｖ2）／（１＋ｖ1・ｖ2／ｃ^2）

　

となり、合成された速度ｖはガリレイ変換の様な線形の変化とは成らず、光速ｃ

に近づくに連れて増加率が減少する、所謂、非線形の変化を行う事となる。

これは、正に、線形速度を前提として構築されたローレンツ変換の結論としての

速度の性質が非線形に変化する事を要請していることに他ならず、前提と結果に

矛盾が生じているという見方が妥当であろう。

この見地で、改めて相対論の速度の加法則を眺めると、この方程式が純粋な線形

速度の概念の元のガリレイ変換に於ける速度の加法則や非線形速度の概念の元の

速度の加法則とは全く異質の形式の方程式である事が解る。

この原因は、相対論の速度の概念が線形性を踏襲しながら速度の上限値ｃを無理

に設定しようとした為であり、線形と非線形の中間の中途半端な速度の概念とな

っている為と考える。

　

特殊相対性理論の代替案として、前提である特殊相対性原理及び光速不変の原理

と共に、速度を線形から非線形の概念に変更して理論の再構築を行う事により、

相対論的効果が生じない論理展開が定量的に確かめられる事になると考える。

つまり、多くの実証実験で確認されている運動中の物体の時間の遅れを思わせる

現象は、速度の非線形（光速ｃを極限値とする円の性質を持った関数）の性質の

現れであり、基本的な物理量である時間や距離や質量は慣性系に依存せず不変量

であり、同時刻の相対性というパッチ処理も必要としない結果を得る事となる。

その為には、ローレンツ変換に代わる新しい座標変換方式の定式化が必要である。

ここで、速度について少し言及しておくと、絶対静止系という基準となる慣性系

の設定が意味の無い事を考えると、速度と言えば、ほぼ相対速度（観測者を基準

とした対象物の速度）の事を指すが、運動中の物質の運動の鈍化が相対的な現象

である事を考えると、この現象が非線形の性質を持った相対速度に起因する事も

ごく当然の事であると納得される。

　

一般的な物理理論の構築の際に、可笑しな結論に達した場合には、論理の展開の

間違いの有無が先ず検討され、これが問題無ければ、最終的に理論の前提となる

仮定の間違いの有無が検討される事（数学の背理法）になるが、特殊相対性理論

の場合には、論理展開の無矛盾性及び検証実験の結果が定量的に理論値と観測値

が偶然にも一致した事で満足し、最後の段階としての前提の妥当性の検討が行わ

れなかった事が、速度の非線形の概念の必要性が気付かれなかった原因と考える。

更には、導出された解が自然現象として正しいと考えられている前提から合理的

に導かれた二次的な隠れた現象であるかどうかという物理学の基本的なチェック

機能が正しく機能していなかった事も指摘されるべきと考える。

つまり、相対論的効果は、前提である光速不変性という光の基本性質が惹起する

二次的な現象ではなく、光の現象とは全く独立した現象であり、論理的な矛盾を

生じない様に論理の展開を行う過程で生じた数学上に必要な抽象的な現象の予想

に過ぎないという事になる。

但し、四則演算が可能な線形数を基本とする現行の数学理論を論理展開の唯一の

極めて有用な道具として利用している現行の物理学に於いて、線形の数を拡張し

て一般化した非線形数を扱える新しい数学理論が全く存在しない事を考慮すると、

今日まで、非線形速度の概念が提出されなかった事は無理からぬ事と思われる。

　

何れにしても、非線形速度の概念が無ければ、相対論の結論にしか到達出来ない

事も事実であり、相対論は、線形速度の概念に於けるベストの理論である事だけ

は否定しようが無いと考える。

更に、相対論という線形と非線形の中間的な速度の概念を基にした理論が登場し

た為に、最終段階（？）の非線形速度の概念の発見に繋ぐことが出来たものであ

り、ニュートン力学の純粋な線形速度の概念から一足飛びに非線形速度の概念に

到達する事は殆ど不可能であるとの感想を持っている。

　

以上の事柄から、特殊相対性理論の代替案の結論は、特殊相対性原理の妥当性を

再確認し更にその適応範囲を拡大する新しい相対性原理を検討する一連の作業に

過ぎず、最早、理論という名称を冠するには値しない様にも思われる。

ここで、巨視的に基本的な物理量（速度、時間、距離、質量）の関係を眺めると、

座標変換に於ける相対速度の変化に応じて、相対論では、全ての基本的な物理量

（時間、距離、質量）が相対的に変化することになるが、相対論の代替案では、

相対速度の変化に応じて影響を受ける物理量は皆無であり、速度の非線形の性質

に応じて物質の運動の鈍化のみが生じるだけであり、座標変換に於ける基本的な

物理量の相対的な変化は全く生じないという事になる。

つまり、ミューオンの崩壊速度（寿命）の延長や動く時計の遅れ等の観測事実は、

時間自体の遅れでは無く、物質の運動の鈍化そのものという事になる。

尚、相対論的質量増加は、時間発展に於ける与えたエネルギー分が質量増加を生

じさせるという実験事実を基に、座標変換に於いても成立すると拡大解釈したも

のであるが、この考えはＣ節で否定されている。

また、運動量保存則を満足させる為に、運動する物質の運動の鈍化分を相対論的

質量の増加で補うことが相対論的質量の概念の主な存在理由と考えるが、元来、

運動量保存則は、ニュートン力学以来の速度の線形の概念の基で成り立つ法則で

あり、非線形速度の概念の基では成立不可のことを考慮すると、相対論的質量の

概念は、その存在理由や根拠を完全に失う事となる。

　

以上の様に、座標変換に於ける基本的な物理量の不変性を考えると、相対性原理

という名称は的確な表現では無く、むしろ慣性系の座標変換に於いても不変とい

う意味から絶対性原理という名称が相応しいとも考える。

なお、座標変換の前提として相対性原理が仮定される習わしがあるが、素光子説

では、従来の相対性原理という公理は前提から外し、素量子の運動状態式が任意

の慣性系で成り立つという事を前提に加えて座標変換を行った結果として、任意

の慣性系に於ける物理法則が全く同一という事が証明されることになる訳であり、

その結果、現行の相対性原理という仮定を証明済みの基本的な法則の部類に加え

る事が相応しいのではないかと考える。

尚、特殊相対性理論の最大の功績は、紆余曲折を辿りはしたが、速度の非線形と

いう自然現象に於ける最も基本的で重要な物理量の性質を見いだす手掛かりを与

えてくれた事であり、更に、自然現象に対する基本姿勢に於ける幾つかの反省点

を与えてくれた事でもあると考える。

　

　この様にして、光と物質の基本的な性質が巧妙に組み合わされる事によって、

自然の姿が、約一世紀振りに、時間と空間の普遍性を基本概念とするニュートン

力学の自然観に回帰することが出来る事となる。

これは、特殊相対性理論のミンコフスキー時空の概念から、空間が平坦で時間が

不変であるユークリッド空間に類似した新しい概念の空間に回帰する事を意味し、

ワイルが１９１８年に興したゲージ理論が幾多の変遷を経て、１９８０年代半ば

にベクトル・ポテンシャルの実在性が実証されるに及んで、実在のゲージ場とし

て４つの基本的な力を統一する有力な理論まで発展してきた事を顧みると、一般

相対性理論の主要な解であるアインシュタイン方程式の重力場が、内山龍雄博士

が提唱する四脚場を導入した一般ゲージ場論で一気に説明できる様になるのでは

ないかと考える。（巻末の参考文献（Ｇ））

つまり、ゲージ場を空間の幾何学的性質の重力場に統合する試みが悉く失敗して

いる原因は、ゲージ場が自然の本質であり、空間の幾何学的なモデルはその一つ

の制限されたモデルにしか過ぎないことを示していると解釈できる。

アインシュタインが一般相対性理論を発表した１９１５年から５年後の１９２０

年のライデン大学での講演で、重力場を表現する時空の性質の拠り所としての新

しい概念としてのエーテルの必要性を説いているが、これこそ宇宙空間に均等に

分布するゲージ場（自由素光子場）の存在をいち早く予測したものと解釈出来る

が、アインシュタインは晩年の大半を自ら創始した重力理論にゲージ場を統一し

ようと固執続けた事は、アインシュタインすら主観的な見方に陥っていた為に、

そこから客観的な見地に移る事が出来なかったというエピソードと解釈したい。

（巻末の文献J）

　

なお、相対性原理が任意の慣性系で生じる事象が全く同じ様に生じる事を要請す

る原理であると考えると、慣性系の座標変換、つまり相対速度に関する変換に於

いて、物質間の相互作用は本質的には電磁気力及び重力が担っている事に注意す

ると、結局、速度を除く全ての基本的な物理量が不変でなければならないという

事を暗に要請しているものと解釈すべきであろう。

但し、距離に関しては、後ほど述べる様に、非線形の物理量であると予想して、

宇宙規模では、ハッブルの法則（遠くの天体の光ほど赤方偏移している）という

非線形距離の性質が表れているのではないかと考えているが、太陽系程度の規模

では、近似的に線形の性質と見なして良いと考える。

又、身近な非線形現象であるカオスやフラクタルやソリトン波や非線形光学等は、

速度の非線形性に由来しているのかも知れない。

森羅万象を理解したいと願う我々の素朴な欲求を動機として、科学が弛まず発展

してきている訳ではあるが、その中核の理論が力学であり、力学の中心の物理量

が速度と考えると、速度が非線形に変化する事から、全ての自然現象は非線形に

変化する現象である事が予想される。

現行の線形速度の概念を基にした力学理論に於いては、大半の現象が線形と解釈

されて、線形理論に於ける厳密解が求められているが、厳密には、非線形理論の

近似解に過ぎないものと考えられる。

一方、非線形現象として扱われている非線形力学理論は、現行の線形理論の基で

は厳密解を求める事が論理的に不可能と解釈されて、近似解に甘んじているが、

非線形速度の概念を導入する事で、厳密解を求める事が可能となる事が予想され

る。

非線形の数の性質に関する研究（非線形数学）が進むと、非線形の数に関する多

くの定理が作られ、現行の線形の物理量を専ら扱っている物理学の多くの問題を

解決する手段が与えられる事になるものと予想されるが、更に、現行の線形数学

自体上の未解決問題を解く鍵を与えてくれる可能性も生じると予想している。

　

Ｅ節（さいごに；素光子一元説）

　素光子の概念の現行の基礎理論への応用について検討し、最終で究極的な目的

として、万物理論としての素光子一元説を視野に入れる事とする。

　

E節＞新しい電磁気理論（荷電粒子の素光子モデル）の提案

　種類の異なる力であっても互いに交換し得るというカントの哲学を信じていた

コペンハーゲン大学の物理学教授のエルステッドは、電場と磁場の間に何らかの

関連性があると考えた最初の科学者であるが、長年の研究の結果、１８２０年に

電流の周囲に磁場が生じる現象を発見した。

この年には、フランスのアンペールやビオ＆サバールが相次いで同じ現象を発見

して数学による定式化を行っている。

アマチュアの物理学者であったファラデーは、１８３１年、磁石をコイルの中に

出し入れすると電流が流れる現象（電磁誘導の法則）を発見し、これまでの力の

遠隔作用の考えを改めて、電気力線や磁力線の概念を考案し力の近接作用を初め

て創案して、場の理論の先駆けとなった。

彼は、電磁誘導の際に、コイルが磁石の磁場の影響下にある場合には、コイルは

何らかの電気的緊張状態となり、磁石を動かして磁場が変動すると、この電気的

緊張度も変化して、それに応じて力が生じ電流が流れるのではないかという卓越

した考えを創案した。

マクスウェルは、ファラデーの電気的緊張度の概念を発展させて、１８５６年、

電気的緊張度をベクトル・ポテンシャルＡとして、電気的緊張度の理論を発表し、

更に、１８６４年には、ファラデーの電磁場理論やアンペールの法則やガウスの

法則等を集大成して定式化した電磁気理論（マクスウェル方程式）を完成した。

１８８４年に、ヘビサイドやヘルツがベクトル解析の手法を用いてマクスウェル

方程式を書き換える際に、電磁ポテンシャルは数学の技巧として使用した架空の

変数であり物理学の実体を伴った物理量では無いという判断の元、新しく再構成

した電磁気方程式から取り去って以来、電場と磁場を唯一の実体と考える電磁気

理論の正当な方程式として現在まで継承されてきている。

　

＜マクスウェルの電磁ポテンシャル（Ａ＆φ）を用いたオリジナルの方程式＞

Ｅ＝−∇φ−∂Ａ／∂ｔ（電場の定義式；ベクトル・ポテンシャルの時間変化）

Ｂ＝∇×Ａ　　　　　　（磁場の定義式；ベクトル・ポテンシャルの回転状態）

　

＜ヘビサイド等がベクトル解析を用いて電磁ポテンシャルを抹消した方程式＞

∇×Ｅ＝−∂Ｂ／∂ｔ　（ファラデー・マクスウェルの式；電磁誘導）

∇・Ｂ＝０　　　　　　（磁束保存の式；磁場には源がない）

∇・Ｄ＝ρ　　　　　　（ガウス・マクスウェルの式；電場の源は電荷）

∇×Ｈ＝Ｊ＋∂Ｄ／∂ｔ（アンペール・マクスウェルの式；電場の変化が磁場）

∂ρ／∂ｔ＋∇・Ｊ＝０（電荷＆電流密度保存則）

　

１９５９年、イギリスのブリストル大学の物理学教授のボームの教室の大学院生

であったアハラノフの博士号論文でベクトル・ポテンシャルの実在性を予言する

アハラノフ・ボーム効果を発表し、直ちに、世界中の研究者が実証実験を開始し

たが、技術的に磁場の影響を完全に排除する事が出来ず、反論に答える事が出来

なかったが、１９８６年に遂に、日立製作所の基礎研究所の外村彰博士が、当時

の世界最高の分解能を誇るホログラフィー電子顕微鏡を使って、超微細加工技術

及び超伝導技術を駆使して完全に磁場の影響を排除する事に成功し、予言通りの

実証実験を行うことに成功した事は、ノーベル賞級の素晴らしい実験と高く評価

されている（巻末の参考文献（Ｑ））が、歴史上最も重要な実証実験と考える。

　

この様にして、ベクトル・ポテンシャルの実在性が疑問の余地無く実証された訳

であるが、不可解な事に、物質という一般的な名称では無く、電子の位相を変化

させる無限小のエネルギーと運動量を有し渦状に回転している何らかの実体とい

う非常に曖昧な概念でしか捉えられていないが、この原因は、素粒子理論の標準

模型（標準理論）が完成し、この理論で物質の基本的な骨組は完全に究明された

という当時の合意された共通の認識があり、ベクトル・ポテンシャルという新し

い余分な概念の物質の参入を無意識の内に拒否した為ではないかと推測する。

また、現行のエネルギーの概念は、無限に細分可能な物理量との基本的な立場を

堅持している為に、ベクトル・ポテンシャルという実証されている運動量を持っ

た実体をストレートに物質と認める事が出来ないというジレンマに陥っていると

も考えられる。

つまり、ベクトル・ポテンシャルを無限に細分可能なエネルギーの集合体という

認識の元では、無限個のベクトル・ポテンシャルを集めないと現実の測定可能な

物理量には成り得ない事となる。

　従って、現行のベクトル・ポテンシャルの概念を変えて、無限小では無くて幾

らかの有限のエネルギーを持った物質という概念に変更すれば、即ち、素光子の

様な最小のエネルギー（エネルギー素量）を持った基本粒子の存在を仮定する事

に他ならない事となり、ゲージ場（ベクトル・ポテンシャル）を量子化したもの

がゲージ粒子としての光子という回りくどい過程を設ける必要もなく、ベクトル

・ポテンシャル（素光子）の集団を光子とするという最も単純な解釈に変更する

事により、現行の理論の多くの困難が氷解するものと考える。

無限大や無限小の概念は、数学上の観念的で抽象的な概念であり、自然界の現象

を研究の対象とする物理学には馴染めない概念と言わざるを得ない。

　ニュートン力学の空間的な広がりが無い位置だけの情報を持った質点の力学や

万有引力を基にした太陽系の惑星を質点と見なしての天体の運行の予測の大成功

により、下部構造を有しない真の素粒子と考えられている電子等の素粒子に質点

という概念を踏襲的に与える事は至極自然の流れではあるが、質点という概念が

エネルギーの量子化の際の無限大に発散する根本原因と考えると、これも物理学

に馴染めない概念と言う事になる。

　

ここで、無限小や無限大に関する数学のこれまでの解決策について述べておく。

ニュートンとライプニッツによって創設された微分積分学は、その根底において

無限小（どんな正の数よりも小さな正の数）や無限大(どんな数よりも大きな数)

といった実数の範囲では定義できない概念を使っており、この状況は18世紀に入

ってオイラーらによって微分積分学が大きな発展を遂げるようになっても改善さ

れなかった。

級数の発散や収束に関する議論には無頓着なままで理論を発展させていった為に、

誤った結論に導かれてしまうことがしばしばあった。

19世紀に入ってコーシーやボルツァーノらによって微分積分学をしっかりとした

基盤の上に再構築しようとする試みがなされ、収束や連続はよりはっきりと捉え

られるようになったが、しかし連続と一様連続の区別はなかったためにコーシー

は自著の中でその事に起因する誤りを犯している。

ε-δ論法は1860年代のカール・ワイエルシュトラスの講義によって完成されたも

ので、これによって無限小や無限大という概念を一切出さずに収束・連続を議論

出来る様になった。

「イプシロン-デルタ論法」　フリー百科事典『ウィキペディア（Wikipedia）』

　

これから、しばらく、電子に関する素光子説の立場からの考察を行う事とする。

電子の古典半径及びスピン角運動量から、電子の表面速度を求める過程を巻末の

参考文献（Ｒ）から転記する。

　電子の質量（有効質量）をm（9.1×10^-31kg）、素電荷をe（1.6×10^-18c）、

真空の誘電率をε0（8.85×10^-12F/m）、プランク定数をｈ(6.63×10^-35J/s),

電子の古典半径をr0(m)とする。

　

一般的に距離r離れた電荷eを持つ２個の荷電粒子の間に働くクーロン力F(r)は、

　

F(r)=e^2/(4π*ε0*r^2)

　

無限遠まで拡散している電場のクーロン力を無限遠点∞から距離rまで距離で積分

すると、その間になされる仕事としての位置エネルギーU(r)が求まり、

　　　 r

U(r)=-∫F(r)dr=e^2/(4π*ε0*r)　・・・（Ａ）

　　　 ∞

電子の自己エネルギー(電子の有効質量mをエネルギーに換算した全エネルギー)が、

半径r0の電子の表面から無限遠点迄の電磁エネルギーを積算した位置エネルギー

U(r0)と等しいと仮定する(つまり、電子の真（芯）の質量がゼロに近似するとす

るが、この事に関しては後に検討する。）と、

　

mc^2＝U(r0)=e^2/(4π*ε0*r0)　　・・・（Ｂ）

∴r0＝e^2/(4π*ε0*mc^2)≒1.0*10^-15(m)

　

因みに、原子の半径（ボーア半径）は0.5*10^-10m程度であるので、古典的な電子

は原子の５万分の１程度の大きさであるという事になる。

　

ここで、巻末の文献（Ｓ）を参考にする。

電子は、電磁相互作用だけでは無く、ウィーク・ボソンを介して弱い相互作用を

行うので、電子が仮想的なウィーク・ボソンを絶えず放出して、近くに相互作用

を行う粒子が存在しないと、ウィーク・ボソンが元のニュートリノに吸収されて

電子に戻るという放出と吸収という現象が繰り返されていると考えられている。

ここで、不確定性原理を利用して、電子の半径を理論的に求めてみる。

仮想的なウィーク・ボソンが存在する時間をΔt、ウィーク・ボソンの速度が光速

cに近似しているとすれば、ウィーク・ボソンの行動距離L＝c*Δtである。

ウィーク・ボソンの質量m_wは1.4*10^-25kgであり、不確定関係から、

　

Δt*ΔE=h/2π

(L/c)*(m_w*c^2)=h/2π

∴L=h/(2π*m_w*c)=(6.63×10^-35)/(2π*(1.4*10^-25)*c)≒2.5*10^-18(m)

　

現行の理論では、電子の半径はゼロと仮定されているが、弱い相互作用を考慮す

れば、電子の半径は、ウィーク・ボソンの行動距離程度という事になる。

そこで、暫定的に、電子の半径r=2.5*10^-18mとする。

　

式（Ａ）で、電子の半径r=2.5*10^-18の場合、式（Ｂ）の右辺の位置エネルギー

Uが2.5*10^3倍になり、左辺の電子の質量mも2.5*10^3倍になる事となり、これは

実験事実と合わなくなり、矛盾を生じる事となる。

この最たるものが、電子を点電荷つまりr=0とする場合であり、Uが無限大に発散

する事となる。

果たして、どの要素が矛盾を生じる原因であろうか？

先ず考えられる事は、式(Ａ)であり、電子自身が持つ電荷による自己エネルギー

が電子の半径に逆比例するという事であろう。

つまり、一般的な常識から考えると、物質の大きさと物質の持つ全エネルギーは

比例関係にある事となるが、電子の自己エネルギーに関しては、正反対の結果を

主張しているからである。

この原因は、電子の半径が小さくなるに連れて電場の密度が際限なく増大する事

にある。

現行の理論では、電荷とは、物質の持つ性質の一つで、質量に対比される性質の

物理量という解釈であり、電気力線のイメージの如く、陽子等の正の電荷を持つ

粒子の表面から四方八方に放射状に電場が拡散（ミニ・ホワイト・ホール？）し、

一方、電子の様な負の電荷を持った粒子は、陽子とは正反対に周りの電気力線が

吸い込まれる様にイメージ（ミニ・ブラック・ホール様？）されている。

つまり、電荷とは、荷電粒子の持つ物理的な性質の一つであり、その表面を基点

として距離の二乗に逆比例する電場を形成する作用を有するという事であろう。

一方、素光子説では、電荷という実体の存在の仮定は必要とせず、電子が捕捉し

ている電場の効果を担う半束縛状態の素光子の総数は一定であり、電子の半径に

は無関係であり、半束縛状態の素光子の密度が、電子からの距離の二乗に逆比例

して減少する事で、素光子場と荷電粒子との相互作用としてのクーロン力が距離

の逆二乗則に従うことを説明する事が出来る。

　

ここで、電子のスピン角運動量がｈ／4πである事が、理論及び実験（１９１５年

のアインシュタイン・ドハースの実験や１９２２年のシュテルン・ゲルラッハの

実験等）で求められているので、これが電子の古典半径r0の元での電子の古典的

な自転運動による角運動量(m*v*r0；vは表面速度）と等しいと置くと、

　

h/4π＝m*v*r0　・・・（Ｃ）

∴v=h/(4π*m*r0)≒2*10^10(m/s)

　

この結果は、電子の自転の際の表面速度が光速ｃ（3*10^8m/s）の約６７倍となり、

物質の速度は光速を超える事は出来ないという相対論の大原則に反する事となる。

尚、この事と共に電子等のフェルミ粒子のスピンが半整数値を取るという事から、

フェルミ粒子のスピンは空間的に２回転しなければ元の位相に戻れないという事

から、フェルミ粒子のスピンは古典的な粒子の自転とは本質的に異なる量子特有

の自由度の表れというよく分からない説明（言い訳？）を行っている。

この結果、現行の理論では、電子の半径を決めかねており、古典半径は少なくと

も間違いであり、ニュートン力学に於ける物質の運動を考える場合の物質の位置

を表すのに最も簡便な重心に一致する質点の概念を踏襲し、点（位置情報のみを

保持し、空間的な広がりを持たない量）つまり、電子の半径rはゼロという解釈が

一般的に行われている結果、電子の電荷に依る自己エネルギー(位置エネルギー）

の無限大の発散という重大な矛盾を来している事に対して、苦肉の策として繰り

込み操作で矛盾を回避している事が現状である。

ところが、電子の半径をゼロとすると、何と！、電子の表面速度が無限大となり、

この後に述べる様に、これこそ非線形速度でも到達不可能な光速ｃに相当する為

に、矛盾を解消する手立てが全く無くなる事となり、電子の半径をゼロとする事

は最悪の選択と言わざるを得ない。

電子は静止質量を有する物質であり、電子の半径がゼロとすると電子の質量密度

は無限大となり、所謂ブラック・ホールを形成する事となる。

　

　ここで、非線形速度を基にした新しい観点からの電子の性質を考察する事とす

る。

線形速度の基での電子の古典半径では、電子の表面速度が光速の約６７倍という

矛盾を生じてしまうが、物質の運動の頭打ち現象に依り、例え絶対壊れない剛体

性の球体を無限大のトルクで自転させた場合でも、球体の表面速度が光速に達す

る事は不可能であろう。

これの本質的な理由は、非線形速度の性質として、質量を有する物質は、無限の

エネルギーで加速したとしても光速ｃに漸近はするが達することは不可能という

論理的な理由が第一であり、束縛状態にある素量子の集合体である電子に於いて、

表面速度が光速に達する寸前に、遠心力に依り電子が空中分解状態となり、束縛

状態から光速で運動する素光子の状態に解放された場合のみ達成される事となり、

実際、電子が空中分解する現象は確認された試しが無い事から、電子の表面速度

が光速に達する事は不可能という事になる。

又、電子自身の運動速度は相対速度であるが、電子の自転角速度は任意の慣性系

に於いて不変に観測されるべきと考えると、任意の慣性系での電子の光の放射と

吸収が等しく行われる事が保証される事となり、相対性原理を強く支持する結果

ともなる。

また、電子の表面速度が一定という事は、電子のスピン角運動量が実験により、

ｈ／４πという一定の値をとる事実（スピン角運動量保存則）の理由を説明する

事になるものと考える。

つまり、無限大まで可能な線形速度を前提とする古典力学に於いては、計算上の

電子の表面速度が光速を遙かに超える事が可能となるが、非線形速度を前提とす

れば、線形の速度の無限大の速度∞が極限値としての最高速度ｃに対応する事と

なり、実際の表面速度は極限値ｃに漸近はするが達する事は不可能という事にな

る。

現行の理論では、電子の古典半径は、電子の自転の表面速度が光速の約６７倍と

いう相対論に反する矛盾を生じる事によって、間違いと断定したが、この結果は、

むしろ、ニュートン力学上の速度（速度は無限大まで許容される）を導出した訳

であり、決してニュートン力学上では矛盾する訳ではなく、その結果をそのまま

相対論で解釈して間違っていると判断した事は二重のミスを犯した事になると考

える。

つまり、ニュートン力学では光速の約６７倍の表面速度に達している様な結果を

得たが、相対論では、質量を有する全ての物質は、光速を超えないという速度の

加法則に従うと、電子の表面速度は、光速ｃに限り無く近づくが光速を超える事

は出来ないという結論から、電子の古典半径に於いても電子の表面速度は光速ｃ

に近い速度に達しているが決して超えてはいないと判断することが妥当であろう。

　

　電子が何故、常に光速に極めて近い表面速度を維持出来ているのかを考えると、

第一の理由はスピン角運動量保存則に従っているというトートロジックな説明と

なるが、これは光の吸収や放出や自由素光子場や電磁場との相互作用による電子

の加速現象が全く無い場合の事であり、電子は常に諸々の外力により加速状態に

ある事を考慮すれば、何らかのスピン角運動量を一定に保つ巧妙な機構が存在し

ている事が推測される。

つまり、外部からのエネルギーの補給を受けることなく、電子自身が光速に近い

表面速度で自転の継続を可能にしている機序を解明する事が必要である。

その一つの解決策として、電子を構成している素量子が光速の運動に復帰しよう

とする復元力が関与しているのかも知れないが、今後の研究課題としたい。

　

光が電子に吸収されたり放出されたりする現象は、光（電磁波の素光子モデル）

を毛糸に例え、電子を毛糸玉に例えると、毛糸を毛糸玉に巻き付けたり解いたり

する光の吸収と放出の機序が直観的に理解出来る事となる。

但し、電子が亜光速で自転している事は事実と考えられるので、電子が光を吸収

する際は、電子という毛糸玉が光速で運動している毛糸を光速に近い表面速度で

巻き取る事により、安定した巻き取りが可能となると考えると、電子の表面速度

が光速に極めて近い事を予想する事が出来る。

そこで、電子の表面速度が光速に極めて近い速度に達している場合を考えると、

電子の表面より僅かに外側に光の衣（誰が命名したか分からないが言い得て妙）

を羽織る事となるが、この状態での素光子の速度は光速を維持している事が予想

される為に、光速より遅い束縛状態の素量子とは成り得ず、電子という荷電粒子

の表面の極近傍を光速で周回している半束縛状態の素光子、つまり電場そのもの

とみなす事が妥当であろう。

すると、裸の電子が光の衣を着た場合は、電場の強度の増加、即ち、電荷の増加

が生じている事が予想される。

つまり、原子核に捕捉されて束縛状態で所定の軌道を周回している電子は、各々

の軌道に対応した異なる電荷を有しているという可能性は如何であろうか！？

　

　電子に働く遠心力は、公転速度と原子核からの距離の積に比例する。

一方、電子に働く向心力である原子核の陽子との間に働くクーロン力は、各電荷

の積に比例し距離の二乗に逆比例する事となるが、電子が上位の軌道に移る際に、

光を吸収して光の衣を羽織る事で電荷が増加し、その結果、クーロン力が増加す

ると推測すれば、任意の軌道での電子の公転速度を一定に保った状態で、電子に

働く遠心力と向心力が均衡する状態を作り出すことが出来るのかも知れない。

つまり、電子の電荷が各軌道で一定値（電荷保存則の一表現）を保っているとす

れば、上位の軌道に移ると、距離の逆二乗に比例してクーロン力としての向心力

が減少する為に、逆に公転半径が増加する分の遠心力の増加との間に力の均衡を

保つためには、公転速度が低下せざるを得ない事となり、この結果、光の吸収と

放射がスムースに行われる事を阻害する結果に終わる事になると考える。

また、電子が光を吸収する際に光の運動量が付加されて加速される（励起状態）

結果、上位の軌道に遷移する事が可能となるが、遷移時に掛かる加速が引き金と

なり制動放射と同じ機序により光を放射して速やかに元の軌道に戻る場合も生じ

るのではないかと考える。

もし、この一連の光の吸収と放射が同一の軌道上で速やかに行われる可能性も有

り、これが物体（反射の方向が揃った場合が鏡）による光の反射ではないかと考

える。

光の吸収又は放射に要する時間は等しく約１０^-8秒であり、反射（吸収と放射）

に要する時間を測定する事で、反射が同一の軌道上で行わたか否かの判定が可能

と考える。

　尚、この一連の光の吸収と放射は、電子の軌道角運動量が保存する形で行われ

ている筈であり、その為には、電子の下位軌道での公転中の或る位置で光の吸収

が行われた場合は、その上位軌道に移った後にその軌道上の或る位置で正反対の

方向に光の放射が行われなければならないと考える。

なお、光の放射が制動放射と同じ機序で生じるとすれば、光の放射方向は円軌道

の接線方向という事になり、光の吸収が光の放出の時間反転の様にして生じると

考えれば、電子の公転運動を追いかける様にして、電子の進行方向と逆の方向で

電子の円運動の接線方向から光が電子に巻き取られる（あるいは光が巻き付く）

様にして光が吸収される事となる事が予想される。

以上の様な予想を裏付ける為には、数式を基にした定量的な遠心力とクーロン力

の計算による力の均衡の有無の検討及び実験による実証が必要である。

　

　ここで、光のドップラー効果を元に、光の吸収と放射を考えてみる。

光源と受光装置との相対速度がゼロの場合は、ドップラー・シフトがゼロとなる

事が実証されている。

そこで、光源とは、一般に発光体全体の事であり、光を放射する電子を指す訳で

は無く、少なくとも電子が属する原子、更には原子を構成要素とする分子を指す

事となる。

光を放射する電子は原子核の周囲を高速で公転しているので、決して属する原子

や分子に静止している訳ではない。

また、受光装置についても、目的の光を吸収する電子を指している訳ではなく、

その電子が属する原子や分子で構成されている受光装置を指す事となる。

この光を吸収する電子も、属する原子に対して光速で運動している事となる。

これらの事柄を考慮すると、光源である光を放射する電子と受光装置である光を

吸収する電子との相対速度がゼロにならない限り、ドップラー・シフトがゼロに

なる事は出来ない。

そこで、この条件を満たす為には、両方の電子の公転速度及びその方向が等しく、

しかも公転面が平行で表面速度も等しい場合のみ、ドップラー・シフトが生じな

い事となる。　　　　　　　　　　　　　　　

但し、これらの条件は、原子や分子の振動現象が生じていない場合という特殊な

条件が前提である。

なお、電子の軌道の公転面及び放射方向に関しては、たまたま一致した場合の光

が受光装置に捕捉されるというだけの事であるが、双方の電子の公転及び自転の

角速度が厳密に一致しなければ、光源と受光装置の間の相対速度がゼロの場合で

も、ドップラー・シフトが生じる事となり、観測結果と一致しない事となる。

以上の理由から、電子の任意の軌道での公転速度が一定である事が実証されれば、

銀河を構成している恒星が一枚の円盤が回転しているかの様に、銀河の中心から

の距離に関係なく一定の速度で公転している不思議な現象を連想させる事となり、

何らかの共通した基本法則の関与の有無を検討する価値があるのかも知れない。

更に、光の衣である素光子の集団が半束縛状態にある事に依り、電子の光の吸収

や放射や制動輻射という光の衣の着脱が容易に生じる事を説明できるのかも知れ

ないが、これらの真偽は、実証実験により決着がつけられる事となろう。

　

電子の質量mは、理論値及び実測した電子の全エネルギーを、エネルギーと質量の

等価式にて質量に換算して得られたものである。

また、電子の古典半径r0は、荷電粒子としての電子の電荷による自己エネルギー

としての位置エネルギーを表現する際に必要となるが、電子の全エネルギーが全

て位置エネルギーと仮定した場合に導出されたものである事に注意したい。

この場合は、電子を構成している要素は、全て半拘束状態の素光子のみ、つまり

電場のみとなり、電子は質量を有する状態には無い事となり、これまでの膨大な

観測結果と矛盾する事となる。

つまり、電子は芯に当たる中心部分に素量子を構成要素とする質量を有する物質

が存在する事が必要となる。

電子のこの芯の部分の質量を芯質量（m_c）と呼ぶことにする。

この芯質量の部分が球体を呈していると仮定して、その半径をr_cとする。

また、電子の質量mから電子の芯質量m_cを引いた残りの質量を電磁質量m_eとする。

　

(電子の全エネルギー；mc^2)

＝(電子の芯質量エネルギー：m_c*c^2)＋(位置エネルギー；e^2/(4πε0*r_c))

　

電磁的質量エネルギー(m_e*c^2)が位置エネルギー（e^2/(4πε0*r_c)）と等しい

と置くと、

　

m_e*c^2＝e^2/(4πε0*r_c)

∴m_e=e^2/(4πε0*r_c*c^2)(kg)

m_c=m-m_e　・・・（Ｄ）

　

結局、芯質量m_cを導出する為には芯質量部分の球体の半径r_cの値が必要となる。

電子の芯の部分の大きさを計測する手段として、或る狭い範囲の空間に閉じ込め

た電子に大量のニュートリノを照射して、その散乱の具合を観測する方法は如何

であろうか？

なお、電子と光の相互作用としてのコンプトン散乱の現象に於いて、散乱断面積

を測定する事が出来るが、この値で電子の見かけの半径としての有効半径を推定

する事も可能であろう。

　

ところで、r_cが古典半径r0より小さい場合には、位置エネルギーが半径に逆比例

する為に増大する結果、芯質量が存在する余地が無くなる為に、r_c＞r0の関係が

必要となる。

この結果は、前に述べた様に、電子の半径が2.5*10^-18m程度でなければならない

という理論値と矛盾する事となる。

この原因も、前に述べた様に、電子の電荷に関するモデルが間違っている為であ

ると考える。

　

電子と同じ電荷量を持つ陽子は、電磁質量が2.1*10^-30kgである事から、電子の

電磁質量も陽子の電磁質量と同程度(2.1*10^-30kg)と仮定すると、式（Ｄ）より、

　

m_c=m-m_e=(9.1*10-31)-(2.1*10^-30)　<0

　

という様に、電子の芯質量が負の値となり、これも矛盾する結果となる。

この原因も、電子の場合と同様に、陽子の電荷に関するモデルが間違っている為

であると考える。

　

陽子の全質量m_pは、陽子の芯質量m_pcと陽子の電磁質量m_peの合計であるので、

　

m_pc=m_p-m_pe=(1.7*10^-27)-(2.1*10^-30) (m)

　

また、陽子の電磁質量と全質量の比:R=(2.1*10^-30)/(1.7*10^-27)≒1.2/1000と

なり、陽子の電磁質量は陽子全体の質量の約千分の１と極めて小さい。

　

電子と陽子の質量比が約1:1800あり、電子の芯質量m_cと陽子の芯質量m_pcの質量

密度が等しいと仮定して、陽子の半径r_pを0.8*10^-15m、電子の芯質量m_cと質量

mの比をkとして電子の半径を芯の半径r_c(2.5*10^-18m)と仮定すれば、

　

m_c=k*m

(r_c/r_p)^3=m_c/m_p=k*m/m_p

∴k=m_p*(r_c/r_p)^3/m

　=(1.7*10^-27)*((2.5*10^-18)/(0.8*10^-15))^3/(9.1*10^-31)≒6.5*10^-5

∴m_c=k*m=(6.5*10^-5)*(9.1*10^-31)=6.0*10^-35(kg)

　

よって、電子の芯質量m_cは、電子の全質量mの約１万５千分の１という僅かな値

となり、電子の電荷を担っている素光子の総数のエネルギー量を質量に換算した

電磁質量は、電子の質量を有する芯の部分を構成している束縛状態の全素量子の

静止質量である芯質量の約１万５千倍という事になる。

つまり、電子の電磁質量を電子の体毛に例えると、電子は大変細身で非常に毛深

いという表現になる。

ここで、電子のシュバルツシルト半径r_sを導出してみると、万有引力定数GをG=

6.67*10^-9(m^2/kg*s^2)とすると、

　

r_s=2*m_c*G/c^2=2*(9.1×10^-31)*(6.67*10^-9)/(3.0*10^8)^2≒4.4*10^-55(m)

　

よって、電子の芯質量に於ける電子のシュバルツシルト半径r_sは電子の芯の半径

r_c(2.5*10^-18m)に比べて非常に小さい為に、電子がミニ・ブラック・ホールと

なる可能性は全くない事となり、これまでのところ、電子の芯質量と芯の半径の

関係は論理的に矛盾するところは無い。

余談ではあるが、現行の重力理論では、電荷に依る荷電粒子のクーロン力が荷電

粒子の半径に依存して限りなく増大するというモデルと同じ考えであり、物質の

質量と距離に依存して重力が限りなく増大する事が可能となり、光さえ重力圏か

ら脱出出来ないブラック・ホールになる臨界の半径（シュバルツシルト半径）を

求める事が出来るが、一方、素光子説が支持するLe Sageの重力理論では、重力は

宇宙空間に存在する自由素光子場の密度に依存する為に、限りなく増大する事は

無く、ブラック・ホールが形成される事も無い。

　

ここで、電子の芯の半径r_cを2.5*10^-18mとして、電子の表面速度vを求めると、

式（Ｃ）より、

　

h/4π＝m*v*r_c

∴v=h/(4π*m*r_c)=(6.63*10^-35)/(4π*(9.14*10^-31)*(2.5*10^-18))

　 ≒2.4*10^12(m/s)

　

この結果は、何と！、光速ｃ(3*10^8m/s)の１万倍の表面速度になる事となるが、

非線形速度の性質を基にしたこれまでの考察により、電子の表面速度は光速ｃに

漸近するが光速ｃに達する事は不可能という事に依り、電子の表面速度は近似的

に光速ｃという事になり、矛盾を生じる事は無い。

但し、電子が担っている電荷の電場としての電磁質量の要素が電子の自転を抑制

する方向に慣性力として働く為に、電子の実効速度は電子の半径を古典半径r0と

した場合の線形速度の基での光速cの６７倍程度に減速しているのかも知れない。

勿論、この場合でも、非線形速度の基では、この電子の実効速度も高速ｃに漸近

した値となる事には違いない。

　

ここで、電子の内部構造を考察する事とする。

電子の芯の部分の体積Vcは、

　

Vc=3πr_c^3/4=3π*(2.5*10^-18)^3/4≒2.7*10-53(m^3)

　

素量子の直径をプランク長Lp(1.62*10^-35m)と仮定すれば、素量子の体積Vは、

　

V=3πLp^3/32≒1.3*10^-106(m^3)

　

ここで、単純に体積比のみから、電子の芯に詰め込める素量子の数N0を求めると、

　

N0=Vc/V=(2.7*10-53)/(1.3*10^-106)≒2.8*10^53(個)

　

そこで、直径2*r_cの球(電子の芯)の中に直径Lpの球(素量子)を最大何個詰め込む

事が可能かという問題(空間の最大充填問題)の結論(約65％)を利用すると、電子

を構成している素量子の論理的な最大個数N1は、

　

N1=0.65*N0=0.65*(2.8*10^32)≒1.9*10^53(個)

　

素量子の質量m0は、エネルギーと質量の等価式であるh(/s)=m0*c^2より、

　

m0=h/c^2≒6.63*10^-35/(3*10^8)^2≒0.7*10^-51(kg)

　

中性子は、半減期が約１０分で自然崩壊し、陽子と電子と反電子ニュートリノ及

び光に分裂する。

　

中性子　⇒　陽子＋電子＋反電子ニュートリノ＋光(0.78Mev-=1.5*10^-37kg)

　

中性子の質量m_nと陽子の質量m_pの質量差m_n_pは、

　

m_n_p=m_n-m_p=(1.67470*10^-24)-(1.67239*10^-24)=2.3*10-27(kg)

　

ここで、ニュートリノ振動の結果生じる３種類のニュートリノの質量を付記する。

　

　　電子（反電子）ニュートリノの質量<2.5eV≒4.5*10^-37kg

ミュー（反ミュー）ニュートリノの質量<170keV≒3.0*10^-32kg

　　タウ（反タウ）ニュートリノの質量<18MeV≒3.2*10^-30kg

　

不可解な事は、亜光速で運動中の互いに変換可能な３種類のニュートリノの質量

が大幅に異なるという事である。

ところで、電子の芯質量と電子ニュートリノの質量を比較すると面白い結果が出

るのではないかと期待したが、現在のところ関連性を見出す事は出来ない。

勿論、電子の芯質量の見積もりを少なくすれば、両者の値が接近する事とはなる。

　

電子の芯質量m_cと電子を構成している素量子の質量m0の比から電子を構成してい

る素量子の個数N2を求めると、

　

N2=m_c/m0≒(6.0*10^-35)/(0.7*10^-51)≒8.6*10^16(個)

　

ここで、１個の素量子が電子の内部空間を占める縄張りの範囲の割合率Oと解釈で

きる、O=N1/N2(≒2.2*10^36)が、電子の内部構造を推測する上で有力なデータと

なると考えるが、素量子のスケールで観れば、電子の内部空間は非常に疎な構造

(隙間だらけ)という事になる。

この結果、自由素光子場に於ける電子は、大半の自由素光子の通り抜け及び希な

衝突により一見ランダムなジグザグ運動を行う事になるのではないかと推測する。

果たして、電子の内部空間は原子の内部構造の様に局在しているのであろうか？

また、束縛状態の素光子（素量子）は、素量子のスケールでは十分な隙間がある

（電子のスケールでの原子の規模よりも遙かに広大）と思われる電子の内部空間

でどの様な状態を保っているのであろうか？

ここで、電子に捕捉されて半束縛状態にある素量子は、どの様な機序で電子に繋

ぎ止められているのであろうか？

素光子が電子の一部を貫通しながら電子の周囲を旋回する事で、捕捉状態が維持

されていると考える事は如何であろうか？

以前、電子をトーラス構造として、その中心の孔を電気力線が貫通してループ状

に電子の周囲を旋回しているモデルが提示されたという事であるが、一考に値す

ると思われる。

素光子説の立場で電子のトーラス構造を考えた場合は、電子に捕捉された半拘束

状態の素光子がトーラスの中心孔を貫通しながらループ状に電子の周囲を旋回し

ている事が予測されるが、更に、電子の中心孔を自転軸として自転している描像

が推測される。

すると、光が電子に吸収される際は、トーラスの胴体の周囲に巻き付く様な状態

で半束縛状態の素光子が周回している描像が考えられるが、この素光子の直接的

な運動自体が、現行の考えである電子の自転に依る磁場の発生と同等の現象が生

じる事となるかも知れない。

これは、電場の運動が磁場を生むという、電子に捕捉された半束縛状態の素光子

の運動方向に及ぼす力（電気力）と異なる方向に動いた場合にその方向に素光子

の運動効果が及ぶ（磁気力の発生）という現行の理論の考えに加えて、素光子の

運動方向に及ぼす力そのものが磁気力として観測されるというものである。

果たして、この様な現象が生じ得るのであろうか？

ところで、現行の理論では、電荷を携えている電子の表面の自転運動で、電荷が

回転運動する事で電荷の運動方向と直角の方向に磁場が生じるという考えである。

ここでも、現行の理論では、電荷をベクトル・ポテンシャルと同様に、物質とは

認めていない事になるが、電荷の効果としての電場も実体の無いものとならざる

を得ない事になる。

一方、素光子説では、電荷なる実体は存在せず、電子等の荷電粒子に捕捉されて

いる半束縛状態の素光子の光速での周回運動自体が電場の効果を生じ、荷電粒子

が運動する際にループ状の素光子の運動に変化を生じる事で、磁場としての運動

効果が生じるという事になる。

なお、電子の自転そのものが磁場の発生に関与していないとすれば、一体、電子

の自転とはどの様な意義を持っているのかという事になる。

但し、電子の軌道角運動量の場合は、電場の効果を担う本態である電子に捕捉さ

れている半束縛状態の素光子の周回運動状態が、電子が軌道を周回する事により

変動させられる事となり、確かに磁場が生じ得ると考える。

大分混沌としてきたが、巨視的に眺める事で新しい知見が得られるかも知れない。

　

　最下位の軌道に居る光の肌着だけを身に付けている電子と最上位の軌道を旋回

している光の衣を幾重にも羽織って着膨れした電子を比較すると、全ての電子の

芯質量は一定であり、着ている光の衣分の電荷やエネルギーや運動量が増加して

いる事になるが、電子の自転は芯の部分の球体（素量子の集合体のみの芯質量）

のみが行っていると判断する事が妥当と考えると、電子の半径は電子の芯の半径

にて一定であり、全ての電子の自転の表面速度が一定である事が説明できる事と

なり、その結果、スピン角運動量が一定になる機序を説明できる事となる。

但し、全くの裸の電子でも、芯質量の約１万５千倍もある電荷を担う半束縛状態

の素光子の集団が羽毛の様に覆っている為に、電子の自転という加速度運動に於

いて大きな負荷が掛かっている事が予想されるが、その結果、実際の電子の表面

速度が線形の速度の基でも光速ｃ程度となっている可能性がある。

電子の表面速度vが光速ｃとした場合(v=c)の電子の見かけの半径をr1とすれば、

式（Ｃ）より、

　

h/4π=m*v*r1

∴r1=h/(4π*m*v)=h/(4π*m*c)=(6.63*10^-35)/(4π*(9.14*10^-31)*(3.0*10^8)

　　≒6.7*10^14(m)

　

よって、この電子の半径r1は、電子の芯の半径r_c=2.5*10^-18mの約２万７千倍の

半径となり、又、電子の古典半径r0=1.0*10^-15mの約６７倍の半径となる。

又、電子の古典半径r0=1.0*10^-15mは電子の芯の半径r_c=2.5*10^-18mの約４百倍

となる。

そこで、電子の光との相互作用に於ける実効的な半径rは、

　

r0（古典半径）≦r（電子の実効半径）≦r1（表面速度が光速ｃの場合の半径）

　

の範囲にあると考えられる。

この電子の実効半径が電子の芯の半径に比べて格段に大きいことが、電子と光の

相互作用の機会を高める働きを担っていると考える事が出来る。

　

尚、金属分子で構成されたマクロの球は、回転速度を上げるに従い次第に分子間

の結合に強大な遠心力による歪みが生じ、光速に遠く及ばない表面速度にて球が

破壊されてしまう事になるが、電子は分子構造どころか原子構造すら無い事を考

えると、光速に近い表面速度に達していても安定した構造を保つことが出来てい

るのではないかと考える。

また、加速器にて光速に近い猛烈な速度に加速された電子の衝突実験に於いても、

電子が安定した構造を保っている事が出来る事を考慮すれば、素量子で構成され

ている電子の内部構造は極めて強固で安定していると考えねばならない。

　

以上の結果、光の衣を全く纏っていない裸の電子の状態から光の衣を纏って最大

に着膨れしている電子に至るまで、電子の表面速度がほぼ光速に近い一定の速度

を保つことが可能となり、全ての電子に於ける光の衣の着脱（光の吸収と放射）

がスムースに行われる事が可能となるのではないかと推測する。

又、光の衣の寸法（波長や振幅や偏光や全長等）が、電子での着脱の過程を経て

も寸分違わず保存する事が必要であると考えると、電子の表面速度が光の吸収及

び放射時にも常に安定した一定の速度を保つ事が必要と考える。

更に、電子の公転により生じる磁場に依り、電子のスピンの方向が或る程度規制

される事が、電子による光の衣のスムースな着脱（毛糸玉の回転による毛糸の巻

き取りと解き）に大きく寄与しているのではないかと考える。

　

尚、電子のみならず全ての質量を有する物質の運動量は、速度の要素を含んでい

る為に、非線形速度の概念の基では、時間発展並びに座標変換に於いて、単純な

加減算を行う事が出来ず、保存する事は出来なくなると考える。

但し、光(素光子の集団）だけは、唯一速度が一定（光速不変の原理）である為に、

時間発展並びに座標変換に於いても運動量が不変となり、任意の慣性系に於いて、

質量を有する全ての物質との相互作用時に、光から物質に一定の運動量が与えら

れる事となり、この結果は相対性原理の妥当性を裏付けるものであろう。

一方、相対性原理の要請から、軌道角運動量やスピン角運動量が時間発展並びに

座標変換に於いても保存する必要がある（角運動量保存則）。

例えば、電子は自転しながら原子核の周囲を公転し、原子の集合体である地球は、

自転しながら太陽の周囲を公転し、太陽も銀河系の一員として公転し、銀河系も

銀河団の一員として公転運動を行い、更に銀河団も運動している事を考慮すれば、

宇宙の或る慣性系から観ると、最初の電子が如何に複雑な運動を行っているかが

想像されるが、この様な大変複雑な運動を介していても、電子の軌道角運動量及

びスピン角運動量が保存しなければならない事になる。

直感的に考えれば、電子の直線的な運動は、相対速度による相対的な運動である

為に保存する事は出来ないが、自転や公転は加速度運動という絶対的な運動であ

り、それ故に保存するのではないかと考える。

　

次に、原子核の周囲を周回している電子の軌道半径の導出を巻末の文献（Ｒ）か

ら転記する事とする。

水素原子の基底状態の時の電子の軌道半径をa（原子の半径程度で、1.0*10^-9m）、

電子の速度をv、電子の質量をm（9.1*10^-31kg）とすると、電子の軌道角運動量

はm*v*aとなる。

原子核の周囲を公転している電子がド・ブロイの物質波の状態にあるとすると、

その波長λ＝h/(m*v)であり、電子が安定して所定の公転軌道を周回できる為には、

物質波が定在波（電子の波長の整数倍が周回距離に一致）となる事が必要となり、

nを自然数として、

　

n*λ=2π*a （n=1,2,3,･･･）　・・・（Ｅ）

　

が必要な条件となる。

そこで、ド・ブロイ波の波長λを上式に代入すると、

　

n*h/m*v=2π*a

∴v=n*h/(2π*a*m)

　

ここで、水素原子の基底状態の時の電子の軌道という事で、電子のエネルギーが

一番低い状態として、n=1と置くと、

　

v=h/(2π*a*m)=(6.6*10^-34)/(2π*(1.0*10^-9)*(9.1*10-31))≒1.0*10^5(m/s)

　

となり、光速ｃ(3*10^8m/s)に比べて、電子の公転速度vは随分遅い事となる。

なお、電子による光の吸収と放射の現象の機序を考えると、公転速度が遅いほど

都合が良い事になると思われる。

因みに、光の吸収及び放射に要する時間Tは約10^-8sであるので、光の吸収及び

放射を行う間の電子の公転回数Nは、

　

N=v*T/(2π*a)≒10^5*10^-8/(6.28*10^-9)≒1.6*10^5(回)

　

つまり、電子が光を吸収又は放射する間に、電子は約1.6*10^5回の軌道を周回し

ている事になるが、周回を繰り返す間に、光の吸収又は放射が途切れる事なく滑

らかに行われなければならない事となるが、果たして、電子の公転運動の動きを

追う様にして、光が電子に吸い寄せられて巻き付くという描像だけで、光の吸収

という現象の説明が事足りるかどうかという事になる。

　

ここで、式（Ｅ）で、最低のエネルギー準位E1を求める為に、n=1と置くと、

　

λ=2π*a=2π*(1.0*10^-9)=6.3*10^-9(m)

∴E1=hν=h*(c/λ)=(6.63×10^-35)*(3.0*10^8)/(6.3*10^-9)≒3.2*10^-18(J/s)

　

このエネルギーE1を質量m1に換算すると、

　

m1=E1/c^2=(3.2*10^-18)/(3.0*10^8)^2=3.6*10^-34(kg)

　

よって、最低のエネルギー準位にある電子は、電子(反電子)ニュートリノの質量

4.5*10^-37kgとミュー(反ミュー)ニュートリノの質量3.0*10^-32kgの中間の質量

を持った光の衣を着ている事となる。

　

ここで、一つの懸案事項として、電磁波の素光子モデルでは、サイクロイド様の

素光子の運動（車輪の回転の様な渦を巻く回転及び車軸の直線的な光速の運動）

を考えると、光の群速度に相当する車軸の光速での運動に加えて、任意の慣性系

に於いて一定である素光子の光速での回転運動を合成すると、何と！、素光子は

光速の２倍で運動している様に観測される事となるが、果たして、この推測は正

しいのであろうか？

例えば、重力場等の加速度系では、加速方向から近づいてくる光の速度は光速ｃ

を超えて観測される事になるが、論理的な最大の加速時には、光の速度は光速の

２倍に近い速度で観測される事になるのであろうか？

素光子の渦を巻く様な回転運動も加速運動であり、電磁波の素光子モデルの場合

の渦状に回転している素光子が論理的に可能な最大の加速運動状態にあるとすれ

ば、渦状の回転速度は光速の２倍の速度に達しているのかもしれない。

なお、素光子が光速で周回運動を行う際に、遠心力で軌道から逸脱する可能性を

考えると、半径が最も小さい円軌道を周回しようとする基本的な性質（向心力と

なり、最小作用の原理の本質か？）を素光子が保持しているとすれば、この力と

遠心力が均衡して軌道から逸脱せずに安定した周回運度を持続している事が可能

となっているのではないかと考える。

この根拠としては、電場としての素光子の運動の軌跡に相当する電気力線が縮ま

ろうとする性質を持っている事が実験的に確かめられている事に依る。

　なお、素光子が周回する最小の半径の円軌道とは、半径がゼロの円運動となり、

これは自転そのものという事になるが、この状態の素光子は宇宙空間に存在する

自由素光子場の素光子という事になり、その直径がプランク長の球体の表面速度

が光速で自転しながら、光速で直進している事が推定される。

　

　重力場を通る光は重力場の勾配に沿って曲がる（重力レンズ効果）事が実証さ

れているが、果たして、電磁場の勾配に沿って光が曲がる（電磁場レンズ効果）

のであろうか？

素光子説では、宇宙空間の自由素光子場の密度の不均衡な状態が、重力場として

観測される事になり、電磁場も荷電粒子に捕捉されている半束縛状態の素光子が

本態と考えるので、重力場と同じ機序にて電磁場でも光が曲がる事が予想される。

もし、このような性質があれば、光は電子の近傍でどの様な振る舞いを行う事に

なるのであろうか？

突拍子もない考えではあるが、電子に吸収されつつある光が、電子の周囲の強大

な電磁場の力により電子に押しつけられる方向に常に運動せざるを得なくなると

すると、光は電子の周囲を光速で周回し続ける事となり、これこそが光の衣を着

た電子という比喩が的を射た表現と言う事となる。

つまり、電子の近傍に来た光が、電子の周囲の強力な電磁場による電磁場レンズ

効果にて電子に捕捉されて、電子の周囲の一定の軌道を光速で周回している描像

が得られる。

これこそが、光も脱出不可能な強大な重力場を形成するミニ・ブラック・ホール

を連想させるものである。

なお、電荷に依る電場の効果を担っている半束縛状態の素光子は、異なる機序で

電子に捕捉されて電子の周囲を周回しているものと考えて良いのであろうか？

つまり、荷電粒子の構造自体の性質により、宇宙の自由素光子場からの素光子が

動員されて素光子の集団が荷電粒子に捕捉されて荷電粒子の周囲を旋回している

状態が、荷電粒子が電場を形成している状態に相当すると考えるが、荷電粒子に

吸収された光は、果たして電場の機能を担っている半束縛状態の素光子の集団の

軌道面とは全く異なる軌道を旋回しているのかどうかという問題がある。

これは、荷電粒子のスピンの方向と光の入射角度との間で、光の吸収の親和性の

差を測定する事で確かめられる事となるが、スピン方向と入射角度が垂直の場合

に最も親和性が高い事が推定され、これが正しければ吸収された光の軌道が電場

の機能を担っている素光子の軌道と平行な回転面を成している事となる。

この結果、電子に吸収された光は波長や振幅や偏光や全長等の基本情報を完全に

保存した状態で電子の周囲を周回し続ける事となり、その光が電子から放射され

る際に全く元のオリジナルの光として再現される機序が簡単に説明される事にな

るのではないかと考える。

公転運動中の電子を追いかける状態で近付いて来た光が電子の円運動の接線方向

に吸い寄せられる様に曲がって来れば、電子による光の吸収の機会が偶然の確率

に比べて飛躍的に高まる事となるが、これは簡単な検証実験で判定可能であろう。

また、電子により巻き取られるというイメージよりもむしろ電子に吸い寄せられ

て来るというイメージの方が正しいのかも知れない。

これは、電気力線を用いたクーロン力のイラストでは、電気力線が電子に絶えず

吸い込込まれているイメージ（ミニ・ブラック・ホール！？）とも共通する。

また、このイメージが正しければ、光という毛糸の先頭の部分だけが吸い寄せら

れる訳では無く、全長が約３０cmの超ロングの毛糸の先頭から末尾まで同じ様に

順番に、約１０^-8秒をかけて電子に吸い取られる事になるものと考えられる。

但し、電子が光を吸い取る約１０^-8秒の時間は、ミクロの現象としては些か長過

ぎるとも考えられるので、原子核の周囲を目まくるしく旋回している電子が全長

約３０cmの光をスムースに吸い取る為には、何らかの巧妙な仕組みが必要である

が、電子の公転速度は超高速であると考えられているので、約１０^-8秒の間に可

成りの公転を繰り返す事となり、その間に全長約３０cmの光の毛糸を首尾良く吸

い取る事は至難の業と思われる。

尚、電磁気力の強さが重力の約１０^42倍（素光子の密度が約１０^42倍？）とい

う強大さ故に、光を吸い寄せる力も強大となり、電子の激しい公転運動にも追従

する事が可能となり、終始安定した状態でスムースに光が電子に吸い寄せられ続

ける事が可能となっているのかも知れない。

また、電子の光の吸収と放射が時間対称で時間反転が可能な現象とすれば、光の

放射も光の吸収と同じ機序で生じている事になるが、今後の検討課題としたい。

但し、新たな問題として、電子が可成りの公転の繰り返しの間は、原子から観た

電子の速度が公転の往復で変動する事から、ドップラー効果にて、光を構成する

一波長の波毎に、波の長さが大きく変動する事が予想されるが、果たして、実際

に波毎に波長の変動が生じているのか甚だ疑問である。

但し、電子に吸収されている光の波毎の波長の変動状態も、光の放射時には逆の

変換が生じて波長の変動が修正（±ゼロ）されてオリジナルの光の状態に復元さ

れる事となれば、何の問題も生じない事となる。

　

ここで、以上の考察の結果、光が重力場で曲げられるのと同様に、電磁場で曲げ

られる事が証明されれば、電子の周囲の強力な電磁場に依り、電子の近傍に近づ

いて来た光が電子に引き寄せられながら巻き付く様に曲がり、電子の周囲を光速

で回旋する様になり、電子の周囲の高密度の電場に挟み込まれた状態になるとい

うイメージが正解ではないかという考えに変わり、最初に考えていた様な毛糸玉

である電子が光速に近い表面速度にて毛糸である光を巻き取るというイメージは

どうも不適切ではないかと考えている。

なお、光自体が電荷の性質を持っていない事が証明されているので、吸収された

光が電荷の増減に関与する可能性は生じないと考えると、吸収された光は、空間

を伝播中の光の波の状態を保ったままで電子の近傍を周回している事が妥当と考

える。

なお、電磁波の素光子モデルの一波長分の波は、半波長毎に素光子の回転方向を

変えている事により、荷電粒子に吸収された電磁波は、荷電粒子の周囲を半波長

毎に逆方向を周回している事となり、この状態の電磁波は、±ゼロという事で、

電荷の強さの増減に関与する事は無い（電荷の保存則の本態）と考える。

すると、２つの光が正面衝突して反粒子同士の対生成（例えば、電子と陽電子）

が生じる際の電荷の獲得時は、同方向に旋回する素光子の集団だけを捕捉する事

に依り、反粒子同士が異なる電荷を獲得する事になるものと推測する。

　

ところで、電気双極子が振動することにより光が発生する現象があるが、巻末の

文献（（Ｄ）の（１４））によると、図（７−２）〜図（７−６）の過程を経て、

図（７−７）では、ループ状に回転している電気力線が束ねられて、トーラス状

になり、細切れになって四方に光速で拡散する事で一波長分の光が発生するとい

う描像になっている。

つまり、１回の振動に付き１波長分の電磁波が生じ、これが振動の回数分生じて、

一連の波が連なる電磁波が発生する事となる。

なお、電場を光として失った荷電粒子は、近傍の素光子場（ゼロ点エネルギー）

から素光子が速やかに補充されて欠員を補う事により、一定の電荷を保っている

と推測される。（電荷の保存則の保証）

ところで、電子を加速器で加速した場合に、加速に関与した電場を携える事によ

り電子の質量が増加する事となるが、電子の電荷が増加する現象は観測されない

事により、電子は加速時に加えられた電場（素光子の集団）を、光（半波長毎に

素光子の回転方向が逆転した状態の素光子の集団）の衣に変換して電子の質量が

増加していると考えなければならない。

すると、電場がどの様な機序により波（半波長毎に反転した運動状態の素光子の

集団）を持った光に変換されるのかという問題が残る事となる。

　

電子と光の相互作用として有名な現象としてコンプトン散乱があり、相互作用の

発生頻度に比例する散乱断面積が求められているが、この数値の解析により、光

が電子に吸い寄せられる様に曲がるかどうかの判定が可能と考える。

なお、物質中を通過する光の速度が真空中の光の速度である光速ｃより低下して

観測される現象や、異なる物質の境界を光が通過する際に光の進行方向が曲がる

屈折や反射等の不思議な現象は、光が物質中の強大な電磁場により進行方向が曲

げられるレンズ効果（電磁場レンズ効果）が原因であると仮定することにより、

簡単に説明できるのではないかと考える。

　光が電子にて吸収と放射が繰り返される事により、見かけの光の速度の低下が

生じるという説明がされている文献があるが、吸収又は放射の際には、約10^-8秒

のタイムラグが生じる事により、ミクロのスケールでは大変長い時間的なロスと

考えると、この現象のみで光の速度の低下を一律に説明する事は困難と考える。

一方、電磁場のレンズ効果を仮定すれば、重力場での光の曲がりに依る実質的な

光の速度の低下と同等な機序で、物質中の光の速度が低下する事を説明できるの

ではないかと考える。（巻末の参考文献（Ｕ））

例えば、チェレンコフ光の発生機序は、電子が着ている光の衣自体が電子の周り

を周回する事により最短距離である周回軌道の直径よりも長い距離を運動する為

に実質的な光の速度が光速ｃより遅い速度で運動している事により、その速度よ

り電子の速度が上回る（例えば、ニュートリノが電子に衝突）と、光の衣が電子

から剥ぎ取られる様に脱落（制動放射）して、電子の進行方向と反対の方向に取

り残される事により生じると考えられる。

尚、裸の電子に於いてもチェレンコフ光が発生する現象が観測される事になれば、

電子の電荷の性質が、電子の周囲を周回している素光子の集団により演出されて

いる事が間接的に証明される事となる。

また、チェレンコフ光を発した直後の電子の質量（全エネルギー）の減少を観測

し、且つ、負の荷電粒子としての性質を失う現象が観測できれば、電荷が素光子

の集団の効果である事が直接的に証明できる事となる。

　

原子内の電磁場を通過する光の動向を具体的で定量的な論理展開を行う事は大変

高度な技術力を要する為に直ちに実行する事は困難であるが、物質中の光の速度

が物質を構成している原子の組成に依存する原子内の電磁場の強さに依り、原子

中を通過する光の曲がりを決定する事が予想されるが、異なる物質の境界面を光

が通過する際の光の屈折率が各々の物質中の光の速度の比に比例するという観測

事実から、屈折率が、各々の物質中の電磁場の強さに依存する光の進路を曲げる

電磁場レンズ効果に依り決定されるであろうと予想する事が出来る。

近接場光（エバネッセント波）という不思議な現象があり、これは異なる屈折率

の物質の境界面で光が全反射する現象において、例えばプリズムの場合に、光の

一部が反射せずに境界面を越えて対側の空気の側に境界面からの距離に関し指数

関数的に強度が減少する様にして光が浸み出す様な現象であり、更に、もう一つ

のプリズムを元のプリズムに光の波長程度の距離に近づけると、浸み出した光が

そのプリズムを透過する様になる現象であるが、これも電磁場レンズ効果の存在

を示唆する現象ではないかと考える。

重力場に於ける光の重力場レンズ効果は、レンズと空気の境界面で光が屈折する

現象と同様に光の軌跡を曲げる作用を有するが、それではレンズを通過中の光は

レンズを構成している石英の結晶中でどの様な作用を受けて光が曲げられるかと

いう事になるが、これ迄の考察により重力場で光が曲げられるのと同様な機序で、

石英を構成している原子内の強力な電磁場（電磁気力は重力の約１０^42倍）に

て曲げられる事となるが、隣の原子との境界では屈折様の曲がり方を行い、各々

原子内を通過する毎に電磁場にてジグザグに曲げられながら進行し、その結果、

光の速度は光速ｃを保っているにも拘わらず、原子内の電磁場の強さや原子間の

位置関係に依存して通過経路が延長する結果、肉眼的には真っ直ぐ進む光の速度

が低下した様に観測されるという事になると考える。

尚、プリズム内の光は直進している様に観測されるではないかという事になるが、

ジグザグ運動様に曲がりくねりながら進行する現象は原子のスケールでの現象で

あり、肉眼のスケールでのプリズムの観測では、直進している様に見えるだけで

あるという事になる。

又、異なる物質（原子内の原子核や電子の構成要素の違いによる電磁場の強さや

分布状態の違い）の境界では光が屈折や反射する様に観測されるが、その本質的

な現象は、異なる物質に依存する光の曲がり方の違いの表れに過ぎないという事

になる。

ところで、現行の幾何光学の理論では、肉眼的に観測されている光の通過距離に

屈折率を掛けたものを光学的距離として、光はこの距離を通過し光の速度は光速

ｃのままという仮定を行う事によって、全ての現象を定量的に説明する事が出来

るという事であり、物質を通過中の光が原子の電磁場で曲げられる事による延長

した光の通過距離が光学的距離に一致する事が予想される。

すると、光学的距離という概念をわざわざ論理展開の都合上使用する必要も無い

事となり、フェルマーの原理（最小時間の原理）の本質も、この様な物質中の光

（素光子の集団）の振る舞いである抵抗がより少ない、つまりエネルギーがより

低い方向に運動する（最小作用の原理の本質）で説明できるものと考える。

　

これから原子内を光が通過する際の光の曲がる現象を定式化し、物質の誘電率ε

と透磁率μで規定される見かけの光の速度ｖがｖ＝１／√εμで表現される事や

ホイヘンスの原理における２種類の物質の境界面に於ける光の入射角と屈折角の

比が２種類の物質中の光の速度（勿論、見かけの速度）の比や光の波長の比にな

る事（sini/sinr=v1/v2=fλ1/fλ2=λ1/λ2）やその他の物質中の光の振る舞いを

全て説明する事が必要である。

なお、フェルマーの原理（光は２点間を結ぶあらゆる可能な経路の内で、経路を

連続的にわずかに変えたときに、その光学的距離（経路を通過する時間）の変化

が起こらないような経路をとる。）は正しいが、この原理を発見した現象である

物質内の光の直進性はあくまで肉眼のマクロのスケールでの現象であり、原子の

ミクロのスケールでは光がジグザグに曲がりくねって走行している事を考えると、

見かけの現象から、幸運にも正しい結果（最小作用の原理や変分原理）を得たと

いう印象が拭えず、複雑な思いに成らざるを得ない。

　尚、冷静に考えれば、そもそもレンズでの光の屈曲現象こそは、レンズの素材

である石英の構成原子内の電磁場中を光が進行する事に依って生じる現象であり、

電磁場レンズ効果という現象はわざわざ新しい名称で呼ぶような新しい現象では

無く、当然の現象という見方が正解ではないかと考える。

ところで、原子中を通過中の光は、周波数が大きいほどエネルギーが大きい為に、

原子の電磁場から受ける力が等しければ、光の持つエネルギーの大きさに逆比例

して加速度が低下する事となる結果、電場中の光の曲がりが小さくなると予想さ

れる。

ところが、プリズムを通過した白色光が空気中に出る際に、振動数が高い単色光

（赤色光よりも紫色光）ほど屈折率が大きく分散する現象があるが、この現象の

発生機序の説明は、境界面での振動数が異なる光の振る舞いを考察する事で説明

可能と考えるが、今後の課題としたい。

なお、白色光よりも周波数が高い紫外線やγ線の場合は、屈折率が１に近くなり、

ミクロのスケールでも、光は直進する傾向が大きくなるという事実がある。

　

ここで、巻末の参考文献（Ｃ）を参考に、荷電粒子に捕捉されている半束縛状態

の素光子の集団（ベクトル・ポテンシャルの本態）で電磁気現象を説明したい。

文献では、電場と磁場の概念を使用せずに、ベクトル・ポテンシャルとスカラー

・ポテンシャルの概念のみで全ての電磁気現象を説明しているが、素光子説では、

電磁場の概念のみならず電磁ポテンシャルの概念をも使用せずに、素光子の運動

力学のみで、全ての電磁気現象を説明する事を試みる事とする。

　

電磁ポテンシャルＡ＆φを基本とする電場と磁場の定義式を再掲する。

　

Ｅ＝−∇φ−∂Ａ／∂ｔ（電場の定義式；ベクトル・ポテンシャルの時間変化）

Ｂ＝∇×Ａ　　　　　　（磁場の定義式；ベクトル・ポテンシャルの回転状態）

　

　先ず、荷電粒子にどの様な機序で自由素光子が捕捉されて半束縛状態を保って

いる事が出来るかという問題があるが、古くから有るトーラス構造の中央の空隙

を素光子が貫通する事で素光子が捕捉状態に保持される事になるという考えがあ

るが、自然の最も単純で最も普遍的な球状構造に対して、敢えて複雑なトーラス

構造を仮定しなければならない事は、自然の基本構造は最も単純であろうと考え

る自然観に逆行するという些か抵抗感があり、今後の課題としたい。

何れにしても、荷電粒子に捕捉された半束縛状態の素光子は、荷電粒子の周囲を

光速ｃの速度で周回しているものと考える。

　

　クーロン力の作用機序も解決すべき重要な課題であるが、以下で説明を試みる。

先ず、前提となる仮定として、スピン角運動量の存在が認められている事から、

荷電粒子は自転軸を中心として何らかの自転を行っていると考えられているので、

この自転軸の向き方により、その電磁気的な性質が及ぶ方向も異なってくるので

はないかと推測する。

　ここで、現在の最も不思議な懸案事項のスピン角運動量による磁気モーメント

の発生機序について、現行の電荷モデルに対し素光子説の立場で推論を試みたい。

現行の理論では、荷電粒子の自転に依り荷電粒子の表面に存在する電荷が円運動

する事に依り運動する電荷の周囲に垂直の方向に磁場が生じるという解釈を行っ

ている。（この説明では、電子は質点では無い事になるが、何の説明も無い。）

また、電磁気力が光速ｃで伝わるという実験事実からも、荷電粒子の表面に存在

している電荷の速度が、正確に光速ｃに達していなければならない事となるが、

質量を有する物質は光速ｃに達する事は不可能という相対論及び素光子説の結論

からすれば、荷電粒子の自転に依るスピン角運動量と磁気モーメントの発生機序

は論理的に無理があると言わざるを得ない。

　

　一方、素光子説では、荷電粒子の周囲を半束縛状態の素光子が旋回している訳

であるが、例えば、その様な状態の電子に仮想のミクロの方位磁石を近づけると、

この電子と磁石の本態である円電流として運動している電子との間で、その回転

の運動方向の違いに依存して電子間に引力又は斥力が働く事になるが、元の電子

を仮想的に固定すると、方位磁石内の円電流の向き（つまり、磁石の針）が安定

する方向に変わる事として、方位磁石の針が或る一定の方向を向く事となるが、

固定された電子の周りに無数の方位磁石を配置してその方向をプロットして繋げ

れば、所謂、磁力線を描く事となり、この状態を以てして、電子の周囲に磁場が

生じていると解釈している事となる。

以上の様な機序にて、電子が自転する必要も無く、電子の周囲に磁場が形成され

ている様に観測される事となるであろう。

つまり、現行の理論での電子の自転に基づくスピン角運動量の獲得に依る磁場が

形成されるモデルに対して、素光子説に基づく電子の自転を必要としないモデル

（電荷の素光子モデル）を提案する次第である。

従って、余談ではあるが、これ迄の素光子説に基づく電子の自転に関する考察の

内容の大半は徒労に終わるかも知れない。

なお、スピン角運動量が、何故プランク定数ｈ（角運動量の次元！）を基本単位

としているかの謎も、素光子の固有エネルギーの推定値がｈ(/s)という事を裏付

ける証拠ではないかと考えている。

また、スピン角運動量が一定値を保つことが出来ている原因は、荷電粒子の電荷

が一定、つまり荷電粒子の周囲を旋回して電場として機能している素光子の数が

一定値を保っている為及び、常に光速ｃで運動している素光子のエネルギー及び

運動量が常に一定値を保っている為と考えられる。

これで、自転角運動量が質量に比例するにも拘わらず、電子と電子の約1800倍の

質量を持ち球体の半径も大きく異なると思われる陽子が、同じスピン角運動量を

持つ原因を説明する事が出来るものと考える。

又、電磁気現象の力が光速ｃで伝わる（場の理論に基づく力の近接作用）事から、

論理的に、全ての荷電粒子の電荷の回転速度（つまり、荷電粒子の表面速度）が

常に光速ｃを保っておかなければならないという問題も解決される事となる。

現行の理論では、電子が自転しなければ生じないスピン角運動量の事実や電子の

表面に存在している電荷が電子の自転による回転が無ければ電子の周囲に生じな

い磁場（磁気モーメント）の事実を、電子の半径を古典半径とすると電子の表面

速度が光速の約６７倍になるという事から質点という最もあり得ない解釈を行っ

ている事情も含めて、どの様に解決するかでジレンマの状態であり、苦肉の策と

して、スピンは電子の自転で生じる訳では無く、量子の持つ内部自由度の一つと

いう解釈に落ち着いているが、この様な不思議なスピンの概念も、素光子モデル

に依れば、全て直観（古典力学）的に理解できるようになると考える。

ここで、現行の基礎物理学の基本姿勢について、言及したい。

量子力学は、シュレーディンガー方程式で一応の基礎が確立された訳であるが、

その結果、この方程式が自然の基本を説明する最終解答と判断し、電子を実体の

無い波動関数で表現する事で、電子の振る舞いを直観的に理解する事が出来ない

状態となり、これこそ、人知を超越した量子力学の神髄という誤解の上塗りを行

い、理解できない現象を量子の持つ基本性質という決して開けて探求してはなら

ないブラック・ボックスに格納し、決して解明する事は出来ないと諦めてしまっ

ているのではないかという憂いである。

この姿勢は、自然現象をエンドレスで探求すべき物理学の基本的な姿勢の敗北と

言わざるを得ないと考える。

　

電子の電磁質量m_eは,全質量m0から芯質量m_cを引いた質量(m0-m_c)であるので、

素量子の質量m0（固有エネルギーをh(/s)jとすると、m0=h/c^2=0.7*10^-51kg）と

置いて、電荷を担って電子の周囲を周回している素光子の総数N_eを求めておく。

　

N_e=(m0-m_c)/(h/c^2)

　 =(9.1*10^-31-6.0*10^-35)*(3^8)^2)/(6.63*10^-35)≒1.3*10^21(個)

　

因みに、電磁波の一波長分を構成している素光子の総数は約１０^8個であるので、

素電荷に相当する電荷を担う素光子の全エネルギー量は、周波数が1.3*10^13Hzの

電磁波（遠赤外線）１個の持つエネルギーと同じという事になる。

　

現行の理論では、荷電粒子は自転する事に依りスピン角運動量を獲得していると

考えられているが、素光子が荷電粒子の周囲を光速ｃで旋回している事により、

荷電粒子が自転してスピン角運動量を獲得している状態と同等な現象が観測され

る事になると考える。

つまり、現行の理論では、スピンは荷電粒子の自転により生じるという解釈をせ

ざるを得ないが、古典粒子の自転とは異なった量子の固有な性質に起因している

との解釈であるが、素光子説では、荷電粒子の自転では無く、荷電粒子の周囲を

光速ｃで旋回している素光子の作用により生じていると考えているので、現行の

理論の全ての問題（特に、スピンの本質的な意味）を解決できるものと考える。

尚、荷電粒子自体は、果たして、全く自転していないのかどうかという事になる

が、目下の考えでは、荷電粒子が自転しない方が、荷電粒子が素光子を捕捉状態

に保持しておく為には都合が良いと考えているが、今後の課題とする。

　

ここで、一つの大きな仮定を行う。

荷電粒子が自転軸を中心として自転している様に観測されるという事に於いて、

自転軸に相当するものは何かという事になるが、荷電粒子を旋回している素光子

が一定の厚さ(素光子の密度の分布状態がガウス分布に従うと推定)の公転面を保

ちながら運動していると推定すれば、荷電粒子の中心を通る公転面に垂直な直線

が荷電粒子の自転軸に相当する事となると考えて、これを仮想的な自転軸と呼ぶ

事とする。

この推定の前提は、素光子が或る公転面を保つ事を可能にする為には、荷電粒子

が素光子を捕捉して、その公転面での運動状態を強制的に保持する何らかの機構

が存在しなければならない事となるが、今後の最重要な解決すべき課題である。

この様な電子や陽子の荷電粒子の極性がどの様にして形成されるのかという素朴

な疑問に対する一つの推測として、素光子の集団である光同士が正面衝突して、

半粒子同士の対生成の際に、素光子の集団が束縛状態である素量子の集団である

質量を有する物質となる時に荷電粒子の極性が形成されるのではないかと考える。

更に、この機構により、電子が光を吸収したり放射したりする機序が説明できる

ものと考える。

更に推測すれば、電子等の荷電粒子が一定の電荷としての半束縛状態の素光子の

集団を捕捉している状態が安定な状態であり、何らかの原因で幾らかの素光子が

脱落すれば、速やかに近傍の自由素光子が捕捉されて欠員を補う現象が生じる事

となり、光が荷電粒子に吸収される場合は不安定状態になり、電子の場合は上位

の軌道に移る事で安定状態になるか吸収した光を放射する事で安定した状態に戻

るかどうかは、電子が置かれている状態に応じてよりエネルギーが低い安定した

状態に移る事で様々な現象が生じているものと考える。

　

例えば、地球の自転軸の一方の極である北極を上向きのスピンに因んで荷電粒子

の上極、他方の南極に相当する位置を下極と呼べば、荷電粒子に捕捉されている

素光子が旋回している方向が地球の自転方向と同じ方向の場合が負の電荷を持つ

荷電粒子に相当し、逆方向に旋回している場合が正の電荷をもつ荷電粒子に相当

するのではないかと推測している。

但し、反粒子同士の対生成や対消滅を考えると、同じ構造で反対方向に旋回して

いる素光子を携えているだけでは無く、反粒子自体の構造上の反対称性も存在し

ていると考えなければならないであろう。

つまり、構造上の反対称性にて荷電粒子の両極が定まり、電荷としての荷電粒子

の周囲を旋回する素光子の旋回の方向（右回りか左回り）が決定されるものと考

える。

尚、現行の理論に依れば、磁極に習い上極はＮ極、下極はＳ極とすべきであるが、

磁場という概念を用いずスピンの概念を継承して、上向きと下向きのスピンから、

この様に呼ぶ事とした。

但し、この上極と下極は構造的に異なり、その結果、上極と下極が逆転する様な

現象が生じる場合は、電場としての性質も逆転する事になると推測している。

又、荷電粒子間の相互作用（クーロン力に依る）の際には、荷電粒子に捕捉され

て公転している素光子の双方の公転面が平行になる様に荷電粒子が向きを変える

（つまり、仮想的な自転軸が傾く）のではないかと考える。

これは、この状態が荷電粒子間の相互作用時に最も安定した状態であろうという

推測に依る。

また、この位置が荷電粒子間の引力又は斥力が最も強く作用する状態でもある。

尚、２つの自由な荷電粒子が対峙した場合は、双方の上極と下極及び下極と上極

が接近する様に、双方の荷電粒子の何れか動き易い方がその両極が入れ替わる様

に、自転軸方向に反転する現象が生じる事に伴って、荷電粒子の周囲を旋回して

いる素光子の旋回方向も逆転する事が生じるものと推定する。

これは、その状態が双方の荷電粒子にとって最もエネルギーが低い安定した状態

であろうという推定に依る。

以上の結果、自由な２つの荷電粒子の間では、スピンの向きが逆の場合（つまり

素光子の回転面も平行の場合）が安定した状態となり、同種の荷電粒子間に斥力

が生じ、異種の荷電粒子間には引力が生じる事となるものと考える。

この極が入れ替わる現象（極の逆転現象）の存在を仮定する事は些か抵抗感が無

きにしも有らずである（実際に実験で認められている）が、荷電粒子の内部構造

が拘わる素光子を捕捉しておく何らかの機構に起因するものと考える。

この極の逆転による荷電粒子の２つの状態が、電子のスピン角運動量が常に２つ

の値、上向きの＋(1/2)*(h/2π)又は下向きの−(1/2)*(h/2π)の何れかを取ると

いう観測結果を説明する現象であると考える。

また、スピン角運動量の値が常に一定値を保って観測される原因も、荷電粒子の

周囲を旋回している素光子の総数が一定値を保って（素電荷の値を決め不変値）、

一定の速度ｃで運動している（光速不変の原理）為であると考える。

又、荷電粒子のスピン角運動量を測定しようとすると、測定機器の原子を構成し

ている電子のスピン状態と相互作用を行い、スピンが安定した状態に変化する事

となり、この結果を測定する事で常に一定のスピンを観測する事になると考える。

余談であるが、非線形速度の概念の基では、質量と速度の積として定義されてい

る運動量は時間発展及び座標変換に措いても保存しないが、角運動量を規定する

角速度は、外部からのトルクが加えられない限りは時間発展並びに座標変換に於

いて不変となり、角運動量も保存する事になると考える。

更に、最も重要な事柄として、電子を始めとする全ての荷電粒子のスピンの向き

が変わるという事は、荷電粒子の周囲を旋回している素光子の運動方向が正反対

の向きに変わるという事であり、その結果、現行の理論では荷電粒子の持つ不変

と考えられている正負の電荷の性質が見かけ上（極の逆転は対峙している２つの

荷電粒子間の相対的な現象）、反対の性質に変化するという事である。

因みに、現行の荷電粒子のモデルでは、スピンの向きの逆転で、荷電粒子の自転

方向が逆転し、スピン磁気モーメントの方向が逆転するが、荷電粒子の電気力線

の方向は逆転しないという事が、素光子説に於ける電荷の機序の説明とは根本的

に異なる事柄である。

尚、実際に荷電粒子が自転を行っている訳ではないが、スピンという物理用語が

慣用的に定着しているので、仮想的な自転という意味でスピンを用いる事とする。

　

なお、原子の一つの軌道には上向きのスピンの電子１個と下向きのスピンの電子

１個しか入る事が出来ないというパウリの排他律も、電子間の安定状態に拘わる

事柄で説明できるのではないかと考える。

この２個の電子の配置を考えると、常に斥力が働いている事から、お互いに最も

離れた距離（つまり、軌道を２分する直径の位置）を保ちながら、或る意味合体

して１個の物体の様に振る舞う事により、この重心の位置が丁度原子核の位置に

一致する様な状態を保ちながら、原子核の周囲を運動している事が予想される。

　それから、フェルミ粒子のスピン角運動量がｈ/2πの半整数倍という事であり、

粒子を空間的に２回転しなければ元の状態には戻れないという大変不思議な現象

の本質的な意味を解明する事が今後の課題ではあるが、一案として、荷電粒子が

仮想的な自転軸を中心に一回転した時点で荷電粒子の上極と下極が逆転し、更に、

一回転した時点で上極と下極が逆転する事により、元の上極と下極の状態に戻る

というシナリオは如何であろうか？

この現象が生じているか否かは、実験により確かめる事で決着される事となろう。

なお、中性子等の電荷を持たない粒子でもスピン角運動量がｈ/2πの半整数倍と

いう事実から、中性子に於いても電荷に依る電場の機能を担う素光子が捕捉状態

となり中性子の周囲を周回している事が予想されるが、正と負の電荷に対応する

素光子が逆方向に周回している事で、電場としては中和の状態となり、荷電粒子

としての機能が消失していると考えると、中性子も空間的に一回転毎にその極が

逆転している事が予想される。

更に、中性子は単独では約１０分間の短い半減期をもって自然崩壊（β崩壊）が

生じ、陽子と電子と反電子ニュートリノ及び光に分裂する事から、中性子は陽子

と電子が反平行のスピン状態による引力で結合状態にある事が推測される。

　

これから、参考文献（Ｃ)に沿って電磁気現象を素光子の運動力学のみで説明する

事を試みる。

　

　最初に、異種の自由な荷電粒子同士が双方の電磁場の影響下にて対峙している

場合は、先ず双方の素光子の公転面が平行となる方向に双方の仮想的な自転軸が

傾き、更に、双方の極が反対側に位置する様に何れかの荷電粒子が回転する事に

より双方の荷電粒子が最も安定した状態となり、相手の荷電粒子の外側を回って

いる自己の素光子の周回方向が相手の素光子の周回方向と一致する為に、素光子

の最短距離を運動しようとする性質（電気力線や磁力線が縮まろうとする性質で

あり、最小作用の原理の本質的な現象と考える）に依り、双方の荷電粒子が近づ

く方向に力が働き、又双方の荷電粒子の間を周回している双方の素光子は逆方向

に運動している状態にある為に、この位置に於ける素光子の密度が減少する結果、

双方の荷電粒子を近づけてその間を狭める方向に力が働く事となり、この２つの

作用が加算される結果、双方の荷電粒子の間に引力が生じる事となる。

一方、同種の自由な荷電粒子が対峙している場合は、相手の荷電粒子の外側を回

っている自己の素光子の周回方向と相手の素光子の周回方向が逆方向となる為に、

この位置での素光子の密度が減少し、素光子のより短い距離を運動しようとする

力が、異種の荷電粒子の場合よりも減少する結果、お互いの荷電粒子を近づける

方向に働く力が減少し、また、お互いの荷電粒子の間を周回している素光子は同

じ方向に運動している事に依り、この位置での素光子の密度が増加しようとする

結果、密度を減少させる方向（荷電粒子間の距離を遠ざける方向）に力が働く事

となり、これらの２つの作用が加算されて、荷電粒子の間に斥力が生じる事とな

ると考えている。

　

ここで、２本の平行な導線で同じ方向に電流が流れる場合は、微視的には２つの

自由電子が平行して同じ方向に運動している状態であり、この状態は正の電荷を

持った陽子に引かれる状態で運動している（電場中の電子の運動）為に、電場の

発生源である陽子のスピンの向きと運動している電子のスピンの向きとは反対の

状態にある事が推測される事となるが、陽子は電子の約１８００倍の質量を有し、

更に、原子核に固定されている為に、陽子のスピンの方向は常に固定状態（歳差

運動を行い多少のスピンの方向のブレがある偏極状態にある）判断すべきであり、

電流としての全ての電子のスピンが陽子のスピン方向と反対の方向に揃っている

状態にある事が推測される結果、電子同士は、恰も異種の荷電粒子間に引力が生

じる機序と同様にして引きつけ合う方向に力が働く事になり巨視的には同方向に

電流が流れる導線間には引力が働く事となる。

但し、この前提は、２つの導線を運動している電子のスピンの向きが同じ状態に

あるという事であり、この状態に関する更なる考察が必要であり、今後の課題と

したい。

また、電子同士が対峙した場合は、各々の電子を旋回している素光子の公転面も

一様に平行となる事が予想されるが、電場の影響下に無い、つまり電流の状態に

無い自由電子同士の場合の様に、双方のスピンの向きが異なる様に変化する力よ

りも、電場に引かれる事（一種の半束縛状態）に依って電子が一斉に同じ向きの

スピンを保つ力が勝る為に、双方の電子の向きが同じ方向を向いた状態のままで

いる結果、異種の荷電粒子間に引力が働くのと同じ機序に依り、電子同士の間に

引力が働くものと考える。

この様に、電場にて一定方向に運動している自由電子のスピンの向きが揃う結果、

自由電子間では引力が生じる事となり、自由電子の運動の乱雑さの主要な原因で

ある格子振動が減少する極低温の状態では、遂には、近傍の自由電子同士が結合

状態となる事が予想されるが、この状態がクーパー対という電子同士が重ね合わ

された結合状態に相当するものと考える。

但し、現行の理論では、クーパー対の双方の電子のスピンは反対向きという解釈

であるが、これでは重ね合わせの状態とは成り得ず、ボース粒子の様に振る舞う

事は出来ないと考える。

格子振動のエネルギーを媒介する仮想粒子のフォノンを介して反発し合う２個の

電子が結合状態となりクーパー対を作る事を説明するＢＣＳ理論があるが、最近

の高温超伝導実験の最高温度が約１３３ｋで、この理論の論理的な予想最高温度

を超えているという事で、現在の高温超伝導現象を説明する新しい理論が待たれ

ているという事である。

また、本当に電子のスピンが反対向きの状態となってクーパー対となっているの

かどうかも、再確認する必要がある。

論理的に考えると、現行の理論に於いても、電流として移動している各々の電子

は、原子核の複数の陽子のスピンの向き（果たして、全ての陽子のスピンの向き

が揃っているか、確認する事が必要）と反対の向きになっていると考えられるの

で、電流として運動している近傍の電子同士も同じ方向のスピンを保っていると

推測する事が道理であり、スピンが反対向きになる為には、陽子からの電場にて

決定されている電子のスピンの状態に対抗して、逆転させるだけの力が発揮され

なければならない事になるが、果たして、この予想が実現されているかどうかを

実験により決着される事を期待したい。

つまり、常温で電圧を掛けて原子核の陽子との間のクーロン力で自由電子が加速

されている状態では、多数の自由電子がこの状態に参加しているが、双方に属す

る素光子の公転面が平行となり、且つ、双方のスピンの向きが反対になる状態に

なっているものと推測されるが、温度を低下させて原子の振動である格子振動を

低下させると、電子のランダムな運動も低下し、参加する自由電子の数も増加し、

電気抵抗も低下する為に、殆ど全ての自由電子の素光子の公転面とスピンの方向

が揃う状態になるが、この状態での近傍の電子間では、双方の素光子の働きにて

引き合う方向に力が働く事となり、電子同士が結合状態になり、所謂クーパー対

を形成する状態となると考える

。

問題は、同じ方向のスピンの状態の電子同士が引力で接近した時に、果たして、

どちらかの電子のスピンの方向が逆転する現象を呈するか否かという点である。

ついでに、超伝導状態に於けるクーパー対を形成している２個の電子のスピンが

同じ方向を向いている事を示唆する実験結果である巻末の文献（Ｄ）を供覧する。

　以上の結果は、現行の荷電粒子のモデルの限界を示すものであり、荷電粒子に

共通する事柄としての同種の荷電粒子間では常に斥力しか働かず異種の荷電粒子

間では引力しか働かないというモデルの制約から逃れられない事が根本原因と考

える。

スピンの作用機序を直観的に表現出来ない事も、現行のモデルの欠点と考える。

更に、重ね合わせが出来るか否かで分類されているフェルミ粒子とボース粒子の

分類法は、素光子説では本質的には間違った分類法という事になる。

なお、超伝導という電流の抵抗がゼロになる本質的な原因は、温度を限りなく下

げる事に依り格子振動が限りなくゼロに近づく為に、電流としての電子の運動が

スムースに行われる事であると考え、本質的な事柄はクーパー対同士が更に結合

して雪だるま式に大きくなり、重ね合わせが可能なボース粒子の様に一塊として

振る舞う様になる事（ボース＝アインシュタイン凝縮状態）であると考える。

更に、ヘリウムの例で、２個の原子がクーパー対と同様な状態となり更にボース

＝アインシュタイン凝縮状態となったものが、超流動現象を生じる事となる。

なお、マイスナー効果（超伝導現象の２大特徴の１つである外部磁場の遮蔽）に

関しては今後の検討課題としたい。

但し、電子がクーパー対化し更に雪だるま式に膨れると、質量も増加する事とな

り、外部の荷電粒子に属している素光子の力が作用しても、ボース凝縮した電子

の運動が容易には変化し難くなる結果、外部から磁場の影響を遮蔽している様に

観測される（超伝導状態の物質に磁石を近づけようとした場合に、磁石の磁極に

関係なく常に磁石に斥力が作用する）というシナリオは如何であろうか？

更に、電圧を掛けない状態の超伝導物質の温度を下げると、超伝導状態となり、

その上に置いた磁石を重力に抗して浮揚させる現象（マイスナー効果）が生じる

場合は、電流による電子のスピンが揃う機会が生じる事がなく、スピンが揃う事

に依るクーパー対を作る機会も無くなる事となり、この状態でマイスナー効果が

生じる機序を説明する事が必要になる。

そこで、超伝導物質の上に磁石を乗せた状態で、超伝導状態になる迄に温度を下

げた場合には、常温では電気抵抗が有る為に、或る閾値以上の電圧を掛けなけれ

ば電流が流れない状態であっても、格子振動が減少する結果、電気抵抗が低下し

て物質に備わっている極僅かな電位差に依り微弱な電流が流れる様になり、自由

電子のスピンが揃う様になって、近傍の自由電子同士が引力で接近してクーパー

対となり、最終的にマイスナー効果が生じるというシナリオは如何であろうか？

ところで、この考えが正しいとすれば、新しい高温超伝導物質の開発に関する新

たな見地からの新しい示唆を与える事となると考える。

なお、超伝導状態では電気抵抗がゼロの状態となり、電圧を掛けなくても永久に

電流が流れる事になるが、電圧を掛けないと同じ方向を向いた電子のクーパー対

の状態が解かれる事は無いかどうか、及び、解かれない場合に温度を上昇させて

超伝導状態が解除された時に、電子のクーパー対がどの様な機序で自動的に解か

れるかどうかという疑問が残る。

　特に２番目の問題は、この次に考える核子間の結合の問題とも関連して更なる

考察が必要であるが、電圧が掛からない状態の自由電子同士では、或る限界距離

より遠い距離では、スピンの向きが逆になる力がスピンが同じ方向でクーパー対

を作る様に働く結合力より強いという事が推測される。

　

　更に、原子核を構成している陽子同士は、電子のクーパー対と同様な機序にて

引力を及ぼし合う事に依り結合状態にあるのではないかと考える。

この状態を保っている素光子の作用が、強い力の作用機序ではないかと考える。

なお、この推論の前提は、核子のスピンの全てが同じ方向を向いている事が必要

（各々の陽子は歳差運動で偏極）であるが、実験により確かめられる事となる。

これを支持する実験事実として、核子間ではスピンが同じ方向を向いている場合

が、異なる方向を向いている場合より引力（強い力）が強くなるという事がある。

また、全ての陽子のスピンが平行状態でなければ、正の電荷の合計が陽子の数に

比例しなくなるという論理上の事情もある。

ところで、陽子と電子が結合して中性子になると考えるのが自然であるが、この

場合のスピンの向きは、引力が生じる為に反平行状態であろうと推測する。

中性子が核子の一員である場合は、陽子に属する素光子が中性子の外側を旋回す

る事により、陽子が中性子を抱きかかえる状態で中性子と引力で結びついている

為に、中性子の自然崩壊を防いでいると考えられるので、中性子が単独となれば、

中性子の構成要素と考える陽子と電子と反電子ニュートリノの結合バランスが崩

れ、所謂、自然崩壊が生じる（弱い力の作用機序）のではないかと考える。

更に、核内の中性子は陽子との間の束縛力より中性子との間の束縛力が弱いとい

う結果から、核子間の結合力は、下記の順番であろうと思われる。

　

核子間の結合力の比較；０≦（中性子同士）≪（中性子と陽子）＜（陽子同士）

　

なお、クーパー対と同様な機序で核子同士が結合状態にあると考えると、各々の

核子の周囲を旋回している素光子を排除して核子が接触する迄接近する様な引力

が生じる事は出来ず、核子間が或る距離（約１０^-15mで、電子の古典半径程度）

まで引力で接近した時点で素光子を排除しようとする引力と核子の近傍を旋回し

て軌道を保とうとする素光子の力が均衡してこの状態で安定し、所謂、強い力の

特徴である「漸近的自由」の状態を保っているものと考える。

更に、中性子を構成している陽子と電子の間も「漸近的自由」の状態を保ってい

ると考えるが、中性子が単独な状態になれば、電子の質量が陽子の質量の1/1800

と極めて小さい為に、電子が安定した状態で長い時間、「漸近的自由」の状態を

保つ事が出来ず、陽子との結合状態から離脱する結果、中性子のβ崩壊が生じる

（弱い力の作用機序）ものと考える。

この推定の正否は、β崩壊の現象を解析する事により判定可能と考える。

この考えを拡張すれば、クーパー対の状態の電子同士も「漸近的自由」と同等の

状態にあり、更には、電子が原子核の陽子に引かれて原子核に高速で落ち込む様

にして近づいても、或る距離（約１０^-15mで、電子の古典半径程度）以内では、

強力な斥力が働く結果、跳ね返される状態（散乱）になるのではないかと考える。

（現行の不確定性原理を用いた説明とは別の解釈）

これが正しければ、海水中に無尽蔵に存在する重水素を原料として電気分解程度

の化学反応を基礎とする夢の常温核融合を実現して、化石燃料（原油や石炭等）

の枯渇が時間の問題である事による深刻なエネルギー危機を回避する為の無尽蔵

のエネルギーを取り出す方法が発見されるかも知れない。（巻末の文献Ｄの12）

余談であるが、細胞内のミトコンドリアは生物が利用できるエネルギーの産生を

司るセンターであるが、マクスウェルの悪魔の役目を担う極めて効率の良い触媒

に特化したタンパク質（究極のマイクロ・マシン）の働きで加速された化学反応

に基づく常温核融合が生じる事によってエネルギーの産生が行われている可能性

がある。

尚、余談であるが、ヤングの二重スリットの実験での、自由素光子場の素光子が

スリットを通過する際に、スリットの縁の原子の電磁場のレンズ効果にて生じる

回折現象を利用して、素光子の密度を高める事でエネルギーを得る可能性を考え

たが、亜光速で運動中の電子に強力な磁場を掛けて発生させる制動放射を利用し

て、電子のエネルギーの大半を占める電荷に関与している素光子の集団を剥ぎ取

る事が

出来れば、一挙に高いエネルギーを得ることが出来るかも知れない。

更に、この電荷を失った電子には、近傍の自由素光子が速やかに捕捉されて周囲

を旋回する事となって電荷の性質が復活し、この電子を加速して制動放射を起こ

す事により、連続して自由素光子を利用可能なエネルギーとして取り出すことが

可能となるかも知れない。（自由電子による自由エネルギーの汲み取り方式）

　

ここで、世俗的な話題として、クレイ数学研究所のミレニアム懸賞問題が有るが、

ヤン・ミルズ理論（クォークを基本粒子とする強い力を説明する量子色力学）に

於ける、「勝手なコンパクトで単純なゲージ群Ｇに対してＲ４乗での量子ヤン−

ミルズ理論が存在し、質量ギャップが存在することを示せるか？」という未解決

の問題があるが、素光子説では、ハドロンがクォークの様な下部構造から構成さ

れているか否かは問題ではないが、少なくとも、電荷に関する基本概念は間違い

と考えているので、ヤン・ミルズ理論の前提が間違っている事となり、その結論

も当然ながら間違ったものになっていると考えている。

核子のスピンの起源として、核子を構成している３つのクォークのスピンが当初

考えられていたが、クォークの関与は約２０％程度という実験結果を、1988年に

CERNのEMCグループが報告し、スピン・クライシス（クォーク理論の危機）として、

核子内のクォーク間を結びつけているグルーオンのスピンに、その起源を求める

研究が続けられているが、グルーオンにもそれだけの効果は無いという実験事実

が分かってきているとの事である。

なお、ついでに、流体力学のナヴィエ・ストークス方程式の一般解の存在の有無

と三次元空間全体に於ける滑らかさを表現できるかどうかの問題があるが、流体

に関する素光子説の立場での新しい見地（特に非線形速度の概念）が加わる事で、

この２階非線形偏微分方程式の解が見つかり、問題が解決される事に期待したい。

（巻末の文献（Ｅ）)

　一方、２本の平行な導線を逆の方向に電流が流れる場合は、同じ方向に流れる

電流とは反対の状態となり、導線間には斥力が働く事となる。

但し、事は簡単では無いと考え、一つの仮定を行う事とする。

つまり、電流の方向と電子の運動方向の違いに習い、荷電粒子間に働く力に限る

とすれば、電子が逆方向に運動している状態は、陽電子が順方向に運動している

状態と等価ではないかという事である。

この状態が論理的に等価という事であれば、同じ方向に流れる電流の場合の導線

間の電子同士が引き合う方向に力が働く事とは反対に、導線間の電子と陽電子間

では斥力が働く事となるものと考える。

なお、それでは、この論法では電子が存在していれば電流（電子の運動）が無い

場合でも、導線内の自由電子間で引力か斥力が働く事になり、巨視的にも、導線

同士に力が働くことが出来る事となり、実験事実に反するではないかという考え

が浮かぶが、実は、電流とは電場の作用にて多数の電子が一斉に同じ方向に運動

している状態である事を考えると、２つの導線を隔てた全ての電子間に同じ方向

の力が一斉に働く事となり、その結果、マクロの構造物である導線間に於いても、

引力又は斥力が働く事となる。

つまり、電流が流れていない状態の各々の自由電子に於いては、電子の仮想的な

自転軸がばらばらな方向を向いている為に、例え他の導線からの力が電子に加わ

ってもその合力は打ち消し合ってゼロに近い状態となり、導線間に力が働くこと

は殆ど無い状態となるという事になる。

　

平行導線間に働く力のパラドックス的な問題が議論される際に、特殊相対性理論

のローレンツ収縮による電場の密度の増加を用いた解釈が一般的に行われている

が、その様な現象を持ち出す必要も無く、そもそも素光子説の解である非線形の

速度の概念では、運動物体の時間の遅れや空間の収縮などの存在の必要もない訳

である。

　

　次に、電流（運動中の自由電子）の近傍に置いた方位磁石が受ける力を考える。

巻末の参考文献（Ｃ）の最後の図を参考にして述べる事とする。

方位磁石が惹起する現象の本態は円電流（原子核の周囲を公転している電子）で

あるので、電子の回転方向に依り、方位磁石の針が向く方向が決定される。

電流の近傍に置かれた方位磁石を構成している原子内で回転している電子に於い

て、電子の接線方向が電流と丁度平行になった瞬間は、電子が電流に最も接近し

た場合と最も離れた場合がある。

前述した様に、同じ方向に流れる２つの電流は双方を近づける方向に力が働き、

反対方向に流れる２つの電流は双方を遠ざける方向に力が働く為に、接近した時

に電子の運動方向が電流と同じ方向の場合は、双方を近づける方向に力が働き、

逆に離れた時には双方を遠ざける方向に力が働く事となり、以上を総合すると、

電子の軌道半径（円電流の半径）を拡大しようとする方向に力が働く事となる。

一方、接近した時に電子の運動方向が電流と逆の方向の場合は、双方を遠ざける

方向に力が働き、逆に遠ざかった時には双方を近づける方向に力が働く事となり、

以上を総合すると、電子の軌道半径を縮小しようとする方向に力が働く事となる。

ここで、以上のどちらの方向が電子の運動をより安定化する方向であるかという

事になるが、これ迄観測されてきた電磁気現象は、全て、前者の電子の軌道半径

を拡大する方向に力が働いた場合である。

これは、後者の場合は非常に不安定であり、速やかに前者の最も安定した状態に

なる方向に変化する（方位磁石の針の回転運動）為であると考える。

尚、電流の周囲に多数の方位磁石を設置すると、電流の方向と垂直の方向に磁石

の針が向き、これを繋げると電流の周囲を一周する方向に並ぶ為に、これを電流

の周囲に右回りの磁場が生じていると解釈されている事になるが、この様な力の

向く方向を繋いだ磁力線という物理的な実体が存在している訳ではない。

　

　最後に、磁場中を運動している自由電子（電流）に働く力については、前述の

方位磁石と電流の関係と全く同様な作用機序である為に、導線は固定されており、

方位磁石の針が容易に動ける状態の為に、方位磁石の針が電流と作用して動く事

となったが、今回の場合は、磁場の発生源となる円電流を作る装置が固定されて

いる為に、電流としての運動している自由電子の方に力が加わり、フレミングの

左手の法則に従って電流及び磁場と垂直の方向に電子が引き寄せられる状態とな

るという事になる。

つまり、対象物の質量の大小が関係する動き難さの度合いや、その他の動き難い

状態を作っている要素の大小により、同じ力が作用しても、動き易い方が動くと

いう単なる力学的な要素が関わる現象というだけの事である。

　

　以上の考察により、荷電粒子間に働くクーロン力により惹起する現象が基本的

な現象であり、全ての電磁気現象はその基本現象が修飾されて複雑化されただけ

の現象であり、クーロン力を素光子の古典力学的な運動のみで説明する事が可能

であると考えている。

また、量子効果と呼ばれている一連の不思議な現象も、対象となる物質が電子等

のミクロの質量が極めて小さい物質である為に、素光子との相互作用が顕著に表

れる事になるだけの事であり、古典力学で扱うマクロな物質も同様な現象が生じ

ているが巨視的に観測する為に目立たないだけの事であり、本質的に異なる現象

では無いと考えている。

　

　荷電粒子（電子）の周囲を素光子の集団がループ状に光速で旋回している状態

が、電荷に依り電子の周囲に電場が形成されている状態に対応すると考えている。

なお、正の荷電粒子（陽子）から負の荷電粒子（電子）に向けて電気力線という

直線が放射状に拡がっている図があるが、これも電磁気現象を理解する上の架空

の概念であり、物理的な実体では無い。

素光子の密度が電子からの距離の２乗に逆比例して低下していると仮定すると、

その密度勾配が電位としてのスカラー・ポテンシャルに相当する事となる。

電子が運動している状態が電流（電子の運動方向と電流の方向は逆）であるが、

電子の周囲を旋回している素光子に、楕円運動の接線方向の速度ｃと電子の運動

速度が合成された速度（光速ｃ！）が生じる事となるが、電子からの等距離に於

けるこの力を繋げると、電子の運動平面上で円を描く事となり、電子からの全て

の位置でのこの回転の運動状態を総合すると、光速で渦を巻く運動を行っている

ベクトル・ポテンシャルとして観測されるものと考える。

尚、これ迄、渦を巻くベクトル・ポテンシャルをダイレクトに素光子の運動状態

と見なしてきたが、素光子の運動状態の二次的な現象がベクトル・ポテンシャル

として観測されるという認識に変わる必要があると考える。

尚、アハラノフ・ボーム効果で電子の位相を変化させるベクトル・ポテンシャル

の働きの本質は、素光子そのものが電子に衝突する事により、電子の速度や運動

方向を変化させる事により電子の位相を変化させている現象という事になる。

（参考文献Q）

　

以上の考察により、現行のベクトル・ポテンシャルとスカラー・ポテンシャルは、

荷電粒子に捕捉されて周囲を光速ｃで旋回している素光子の集団が惹起する現象

を表現した概念であり、荷電粒子に静止している系では、静電場の電位の意味と

しての素光子の密度の勾配をスカラー・ポテンシャルという概念で捕らえ、一方、

荷電粒子が動いている系では、素光子の旋回運動状態をベクトル・ポテンシャル

という概念で捕らえているという事になる。

そこで、ベクトル・ポテンシャルを４つの基本的な力の源（ゲージ場）と位置づ

けている現行のゲージ理論に対し、更に本質的な唯一の基本粒子と考える素光子

を基に新しい統一理論の構築が必要であり、その結果、現行の基礎理論に関する

行き詰まっている多くの問題の解を与えることが出来る様になるものと考える。

　

素光子説の立場での今回の電磁気現象の考察では、重要な４つの結果を得る事が

出来たと考えている。

１つ目は、重力場中の光のレンズ効果と同様に、電磁場に於いても同様な強力な

レンズ効果が生じると仮定すれば、物質中の光の速度の低下や屈折や反射の機序

や電子に光が吸収されて保持される機序が簡単に説明できる可能性がある。

２つ目は、荷電粒子の電荷による現象を、素光子が荷電粒子の周囲を旋回してい

る事で説明できる目処が出来た事である。

その結果として、スピンの謎の解明に大きく前進した事であり、最後の１つは、

強い力の源としての電子同士のクーパー対と同様な機序にて、核子のスピンが同

じ方向を向く事による陽子間や陽子と中性子の間での引力の発生の可能性である。

これらの推論の正否は、実験により決着可能と考える。

ところで、最後に残った最大の謎は、どの様な機序で素光子の集団が荷電粒子に

捕捉されて荷電粒子の周囲を光速で旋回しているのかという問題である。

ベクトル・ポテンシャルは常時渦を巻く運動を行っているという第１印象がある

が、素光子は、渦を巻く様な運動を行う極性の様な基本的な性質を有していると

いう解釈で良いのか、又は合理的な説明が可能な二次的な運動状態という事であ

るか、今後の重要な検討課題である。

なお、荷電状態にある荷電粒子は、周囲に旋回状態を形成している素光子の集団

が存在しているので、荷電粒子の近傍を通過する光（素光子の規則的な集団）が

相互作用により荷電粒子の方向に吸い寄せられる様に進路を変える事（荷電粒子

自体もこの光に吸い寄せられる様な運動を行う）となり、或る臨界角度を超える

と、荷電粒子に捕捉されてその周囲を旋回する軌道をとる様になるが、この現象

が光が荷電粒子に吸収される現象として観測される事になるもの

と考える。

更に、荷電粒子から光が放射される現象は、荷電粒子の加速運動の際に荷電粒子

の周囲を旋回している光が、荷電粒子の束縛力よりも加速運動による慣性力が勝

る場合に、荷電粒子から振り落とされる事で生じるもの（制動放射）と考える。

　

電子のスピンは観測されて初めてスピンの方向が確定し、観測される迄はスピン

の方向は不確定という解釈がなされているが、スピンの方向を観測する際の磁場

の影響を受けて、より安定したエネルギーが低い方向にスピンが向く結果を観測

しているのではないかと考えると、電子のスピンは元々確定した運動を行ってい

るが、観測という相互作用を生じる操作がアーチファクトとなり観測前のスピン

の状態を把握することが出来ないと言う事だけに過ぎないのではないかと考える。

これは、正しく否定的な立場でのハイゼンベルクの不確定性原理を地でいく現象

ではないかと考える。

物質の物理量は測定というアーチファクトを通して検出する事となるが、マクロ

の物質の場合は測定値に影響を与えるアーチファクトの割合が概して極めて低い

事が多く、アーチファクトを考慮しなければならない事態は少ないが、ミクロの

物質の場合はアーチファクトの割合が相対的に大きくなり、測定値が大きく変動

する事を常に考慮することが必要である事を考えると、不確定性原理の思考実験

も併せて、観測されるまでは不確定という考えは、物質が不確定な物理量（取り

得る可能性の全ての重ね合わせの状態）を有するという奇妙な状態の物質が果た

して存在しているのかというシュレーディンガーの猫の例の様な素朴な哲学的な

問い掛けに対し、どの様に回答するつもりであろうか？

これは、観測という人為的な行為の影響を余りにも過剰に意識した結果ではない

かとも感じられる。

この問題に関連して、光のドップラー効果に於けるドップラー・シフトは、光源

と観測機器の相対速度に依り決定される事となるが、それでは観測機器に捕捉さ

れる前の空間を伝播中の光の波長は不確定な状態であると考えなければならない

のかという素朴な疑問が生じる事となるが、別枠でＥＰＲ論争に関連して私見を

述べる事とする。

　

原子に束縛されている電子から放射される電磁波の放射時間は約１０^-8秒である

ので、電磁波一個の全長つまり毛糸の長さは、意外と長く約３０cmとなる。

つまり、電磁波一個のエネルギーは極めて小さくミクロの世界のレベルであるが、

その長さは我々と同じスケールのレベルであり、他のミクロの質量を有する物質

と比較して特異な存在（果たしてミクロの物質かマクロの物質か！？）と言う事

が出来る。

蛇足であるが、論理的に最低の周波数は電磁波の放射時間である約１０^-8秒間に

１個の波が生じる場合であるが、この場合の周波数は約１０^8Hzという事になる。

　なお、荷電粒子に自由素光子が捕捉されて電荷を獲得する機序は不明であるが、

電子の首振り運動現象（スピン）の存在を考えると、電子の周囲の半束縛状態の

素光子がランダムに電子を周回している訳では無く、一般的な球体が自転する際

の自転軸と呼べるものを中心として電子の周囲を一定の方向に周回しているので

はないかと考えるが、素光子の周回する方向の違いにより、正と負の電荷の違い

が生じるのではないかと推測する。

この描像により、クーロン力（同種の電荷間での斥力、異種の電荷間での引力）

を素光子という粒子の単純な運動力学的現象で説明出来る可能性がある。

　

荷電粒子の電気力の方向を示す電気力線は最短の長さに縮まろうとする働きを持

っている事が実験により認められているが、この現象は、荷電粒子の周囲を周回

している半束縛状態の素光子が最短の距離を取ろうとする基本的な性質の表れで

あると解釈すると、この性質に起因する力が荷電粒子同士の引力と斥力を生じる

根本的な原因であると考える事が出来る。

又、この現象は、光は軌跡が最小となる経路を取ろうとするフェルマーの原理や、

質量を有する物質は作用が最小になるような運動を行うという最小作用の原理を

生じさせる本質的な性質ではないかと考える。

　

荷電粒子の持つ電荷が一定の値として観測される機序としては、電荷を構成して

いる半束縛状態の素光子が何らかの原因で半束縛状態から離脱した場合は、近傍

の自由素光子が荷電粒子に捕捉されて半束縛状態になる事によって、その欠員を

速やかに補充する役目を果たして、荷電粒子の電荷を構成している素光子の総数

が一定に保たれているのではないかと推測する。

電子と陽電子等の荷電粒子の対生成の場合には、生成直後は荷電状態では無く、

光子を構成している素光子の集団の残りが荷電粒子に捕捉される形で半束縛状態

の素光子の集団となり、電荷が獲得されるのではないかと推測する。

正の荷電粒子（例えば、陽子）と負の荷電粒子（例えば、電子）が出会えば、お

互いに引きつけ合う事になるが、周囲の電場は±ゼロとなり電場が消失した様に

観測されるが、単に電場の電位勾配が平坦化してゼロになっただけであり、電場

の本態である半束縛状態の素光子の空間密度は２倍となり、素光子の密度勾配が

消失して平坦化してゼロとなるという事である。

これ迄、電磁気現象を素光子説の立場で定性的に論証してきたが、今後は、数学

を用いて定式化し、定量的に電磁気現象を論証し、実験事実と矛盾しないか否か

を検証する事が必要である。

最後に、荷電粒子にどの様な機序で素光子が捕捉されて、荷電粒子の周囲を周回

する様になるかは、目下のところ不明であるが、電子とその反粒子である陽電子

の場合の様に、電荷の符号のみが異なり、その他の物理的な性質が同じという事

は、荷電粒子の周囲を周回する素光子の公転方向が異なるだけではないかという

推測が可能となり、何が公転方向を規定しているのかを検討する必要がある。

但し、このままでは余りに漠然としており、手掛かりを掴む事は困難と考えると、

光同士の正面衝突で電子と陽電子の対生成が生じる現象まで遡り、光速で運動中

の素光子同士がどの様な過程を経て束縛状態になるかを、例えばコンピューター

・シミュレ−ションを用いて解析する事により、電子や陽電子の立体構造を推測

する事が可能となり、荷電粒子が一定の方向に周回する素光子の集団を捕捉して

おく機序が解明できるものと考える。

　

E節＞素光子工学と素量子工学の創設

　アインシュタインの有名なエネルギーと質量の等価の式；Ｅ＝Ｍ*c^２や光から

電子と陽電子が対生成される現象や、反粒子同士の衝突による対消滅及びその全

エネルギーに相当する光が発生する事実を考える時、物質とは光が固まったもの

ではないかとの素朴な印象を抱かずにはおれない。（素光子説の発端）

又、光が物質の境界面で全反射する場合の所謂、エバネッセント光の発生の現象

は、電子の表面に衝突した光（素光子の集団）が束縛状態の素量子群に一旦変わ

るが、安定状態に成れずに直ちに光（素光子の集団）の状態に戻る過程と考える

事が出来よう。

これからの夢として、自然には存在しない新しい物質（人工の素量子の集合体）

を作り出す技術の研究（素量子工学と命名）が進むと、最も効率良いエネルギー

源としての新しい燃料となる粒子を創世する事も可能になるかも知れない。

又、素光子の集団である光も、素光子の構成形態を様々に変化させる技術が確立

（素光子工学と命名）すれば、人工的に創造した光と物質の相互作用時に生じる

自然界には存在しない全く新しい現象を作り出す事が可能となるかも知れない。

なお、物質の対生成の場合は、光の構成要素である素光子の集団がサイクロイド

様の運動を行い、半波長毎に回転の向きが逆転する事により、素光子の集団同士

が、お互いに相手を巻き込む様に、又、抱き付くような状態を通して、安定した

束縛状態を形成できるのではないかと推測する。

又、反粒子同士が同時に生成される機序として、或る方向に巻き込む現象と共に、

その反対の方向に巻き込む現象も同時に生じる結果、それぞれの粒子が反粒子と

しての性質を獲得するのではないかと推測する。

これは、日本の巴の構図を連想させるが、数学の双対性も関連し、現在素粒子と

位置づけられている電子やニュートリノの内部構造を推定する大きな手がかりと

なるものと考える。

そこで、反粒子同士の本質的な違いは、反粒子を構成している素量子の配列の違

いであり、量子の持つ内部自由度としてのスピン（自転角運動量が(ｈ/２π)/２

を単位の半整数値）も同じ原因（例えば、クラインの壺の概念に似た二重構造）

から生じているのではないかと推測する。

　

E節＞荷電粒子を媒介とする自由素光子場からの自由エネルギーの取り出し

　電子や陽子等の荷電粒子は電荷というエネルギーを有しているが、電荷が荷電

粒子の周囲を光速で周回している半束縛状態の素光子の集団であると仮定すれば、

制動放射やチェレンコフ光の発生機序の様にして、電荷を何らかの方法で効率良

くはぎ取る事で自由エネルギーとして利用できる可能性がある。

なお、電荷をはぎ取られた後の荷電粒子は、近傍の自由素光子場からの電荷とし

ての半束縛状態の素光子の集団が速やかに供給される事で元の電荷を持つ事とな

り、この過程を繰り返す事で、宇宙空間から利用可能な無尽蔵な自由エネルギー

を連続的に取り出すことが出来る可能性があるが、技術的な問題としては電子を

如何にして効率良く加速させる方法を考案出来るかどうかという事になる。

　

E節＞量子力学に於ける量子現象に関する素光子モデルに依る解釈

　ド・ブロイは、アインシュタインの光量子という粒子の性質を持った素粒子が

波動という性質を併せ持っているならば、電子等の粒子も波の性質を併せ持って

いても可笑しくないとの奇抜な発想の元に、光子の波動の性質を表している光子

のエネルギーＥ＝ｈνと運動量ｐ＝ｈ／λを利用して、質量のある電子等の物質

の粒子の性質に波の性質（ド・ブロイ波）を付加する考えを１９２４年に発表し、

これに啓示を受けたシュレーディンガーがこの考えを１９２６年に波動方程式と

して発表したが、この方程式の解は、量子の不思議な振る舞いの舞台である原子

レベルのミクロの現象を悉く説明する事が出来る事が実証されるに及んで、量子

力学の最も基本的で重要な方程式と高く

評価されている。

　

　ここで、素光子説の立場で、ド・ブロイ波の本質を少し考察したい。

先ず、光子のエネルギーｈνから類推して、電子等の量子のエネルギーをｈνと

仮定した意味を考えると、量子は振動数νの振動を行っており、そのエネルギー

がｈνという事である。（巻末の参考文献（Ｔ）参照）

振動数νの光子は、固有エネルギーがｈ／ｓの素光子がν個（何らかの整数化の

処理を行う）集合している事に相当している事から類推すると、振動数νの振動

を行うド・ブロイ波の性質を持つ量子は、ν個の素量子（束縛状態の素光子）の

集合体であると考えられる。

更に、光子の振動は、光子を構成している素光子１個１個が回転運動という一種

の振動状態を呈する結果、全体としてν個の素光子が一斉に振動していると考え

ると、光子の振動数νの意味の別の解釈が出来る事となり、これを他の量子にも

拡大すれば、素量子１個１個が揺れ動いている事で、ν個の素量子の振動が全体

として固有の振動数νで実際に振動している様に観測される事になると推測する。

なお、シュレーディンガーは、ド・ブロイ波（量子の振動）の考えを発展させて、

電磁波と同様な波動の性質を量子に持たせる拡張を行い、実際の波の描像を持っ

た波動方程式を作った訳であるが、この波動関数が実際の波を表現しているのか

どうかで問題となり、量子の存在位置の確率を表す関数（確率波）であるとする

ボルンの解釈で一応の決着が付いた事になっているが、素光子説の立場でもこの

事に関しては部分的に同意するところである。

但し、最大の問題点は、確率波即、量子が運動中には確率的な波の状態であると

解釈している事であり、数学上の架空の波を物理学上の実在の波と解釈した事は、

論理の大飛躍と言わざるを得ない。

　

素光子説の立場では、光のモデルとしては、電磁波がほぼ忠実にモデル化を達成

しているが、光子は限定された条件の基での粒子性に重きを置いたモデル化であ

り、光の持つ自然現象を全て忠実には再現出来てはいないと考えている。

一方、量子のド・ブロイ波という振動しながら運動している光子に似た描像は正

しいと考えるが、更に波動の性質を付加する考えは、実在の波が否定されている

結果、光子のモデルと同様に論理の飛躍との感を強くする。

つまり、量子は、自ら振動し限局した領域でアメーバ様に絶えず形を変形させて

運動しているのかも知れないが、決して全空間に拡散する様な波動の性質は持た

ないものと考える。

なお、光子を振動数νで振動しｈνというエネルギーを持った粒子とする描像は、

電磁波の描像と大きくかけ離れていて余り適切なモデル化とは言えないが、この

不適切な光子の描像から類推した振動する粒子という電子の描像が極めて適切で

ある事を考えると、大変皮肉な結果と言わざるを得ない。

　

　波動の概念について付け加えると、水波や音波は、それが伝わる媒質としての

水分子や空気を構成している窒素や酸素等の複数の分子が、バケツ・リレー的に

玉突き運動にて波動を伝える為に、媒質が存在する限りは減衰はするものの際限

無く波動が伝わるが、光の場合は素光子場の素光子とは正面衝突する機会は極め

て希にしか生じることが無く、更には素光子場の素光子同士が玉突き運動を行う

機会も大変希と考えると、素光子場が媒質とは成り得ず、光自らが光速で運動し

ている状態だけであり、百数十億光年彼方の天体から放射された光が殆ど減衰す

る事無く遙々地球に届く事を考えると、光の波の構成要素としての電場と磁場が

宇宙空間に無限に拡散する事などあり得ないものと考える。

　

なお、宇宙空間に存在する素光子場を大海に例えると、光が大海を運動中に潮流

とも言うべき素光子場の密度の勾配に出会うと、光の構成要素の素光子と素光子

場の素光子の衝突とは異なる機序で恰も潮流に押し流される船の様に、光の軌跡

が曲げられる現象が生じる事が想定されるが、素光子場の密度の勾配こそが重力

という引力を生じる原因（重力場の勾配）であり、この節の後で述べるLe

Sageの

重力理論が素光子場の密度の勾配を生じる機序を与える有力な理論ではないかと

いうシナリオを描いている。

　

電子についても、波を伝える媒質など無い事を考えると、電子の波動が宇宙空間

に無限に拡散するという考えは根拠のない大きな論理の飛躍と言わざるを得ない。

また、波の固有の性質として水の波を例に取れば、波がスリットを通過する際に

回折現象を生じ、更に波同士が干渉現象を生じるという事であるが、水波や音波

は水分子や空気の成分である窒素分子や酸素分子等の粒子の集団が共同で規則的

な流体力学上の運動を行う事により達成されている事を考えると、波の性質とは

グローバルな集団の現象と捉える事が妥当であり、素粒子である量子の基本的な

性質として波の性質を仮定する事は些か的外れの想定ではないかと考える。

また、スリットでの回折現象も、水分子や電子という一個の粒子の固有の現象が

無ければ、集団としての回折現象も生じないと考えると、回折現象は波の性質を

表した現象であり粒子の性質の現れでは無いという解釈も誤った判断と考える。

　

　量子力学は、素粒子レベルでの自然現象を記述する数式に於いてプランク定数

ｈが登場する事を考えると、潜在的に素光子（及び素量子）のエネルギー不変の

原理をその基本概念に据えて発展してきたものと考える事が出来る。

ここで、量子論の諸問題を列記して、素光子説の立場での解釈を試みたい。

　

（１）不確定性原理

光子や電子等の素粒子（下部構造を持たない粒子）の持つ基本的な性質として、

正準共役な物理量である位置の本質的な誤差Δｑと運動量の本質的な誤差Δｐの

間には、Δｑ＊Δｐ＝＞ｈという不等式が成り立つ不確定な関係が存在するとい

う解釈がなされている。

素光子説では、素粒子と考えられている全ての物質が素光子の集合体という立場

であり、その結果、素粒子が統計的で確率的な振る舞いを行う事が当然予想され、

この現象が不確定性原理に従うように観測されるという解釈が可能かも知れない。

不確定性原理の一方の正準共役な物理量であるエネルギーと時間の誤差の不等式

（ΔＥ＊Δｔ＝＞ｈ）が真に意味するところは自然の基本性質が不確定な要素を

内在しているものではなく、自然界に存在するエネルギーの最小の単位（素量）

を暗に示すものであり、細分化の限界値と不確定性原理の誤差の限界値とは等価

ではないかと思われる。

具体的に述べると、不確定性原理の不等式から素光子や素量子の固有エネルギー

をｈ（／ｓ）と仮定している訳であり、素光子の集団である光や素量子の集合体

である質量を有する物質は、常に構成要素の個数を一定に保っている様な理想的

な状態ではなく、通常は構成要素の個数にばらつきを持った状態であり、最小の

ばらつきが１個の要素である事を示しているに過ぎないのではないかと考える。

つまり、自由素光子場を原材料とすると、素光子の集団である光や素光子の束縛

状態である素量子の集合体が作られる際に、規格通りの理想的な原材料の個数で

構成される事は希であり、通常は個数にばらつきが生じ、最小のばらつきが構成

要素としての素光子一個という事になるという考えである。

　

　１９２６年に登場したシュレーディンガー方程式の本質を確率波と解釈して、

電子は確定した空間に存在している訳では無いとするボルンの考えに反対してい

たシュレーディンガーは、自ら創始した波動方程式を基礎とする波動力学に欠如

している電子の運動の道筋の記述を表現可能な新しい量子力学の方程式の構築を

模索し、１９３１年に確率過程論の先駆けとなる論文を発表したが、理論を支え

る道具としての数学が未熟であり、理論の構築でも未完成のままとなった為に、

物理学の主流派からは余り注目されないまま忘れ去られた状態となっていたが、

物理学よりもむしろ数学の分野でこの理論が地道に研究され、チューリッヒ大学

の数学教授であった長澤正雄博士等の着実な研究の結果、シュレーディンガーが

当初目論んでいたが生涯果たせなかった新しい量子力学の基盤である確率過程論

の一応の成果が上げられているが、何故か、この領域のネルソンの確率量子化法

が有名である。（参考文献Ｈ）

宇宙空間に均一に存在する自由素光子場を想定すると、素光子との相互作用によ

る量子の揺らぎ（電子のジグザグ運動等であり、ブラウン運動と類似の現象）が

生じている可能性があり、確率過程論の前提の電子のランダムなジグザグ運動の

存在を裏付ける事が出来るものと考える。

　

　量子論の発展の過程でのボーアの対応原理（高エネルギーでの電子の振る舞い

が古典粒子の振る舞いに近似して観測される）は、正に古典力学のブラウン運動

を惹起する花粉の微粒子（量子力学に於いては電子）よりも巨大な物質(古典粒子

に対応)のブラウン運動（古典力学で記述される運動）を生じさせるに足る水分子

の運動エネルギー（量子力学に於いては素光子場の運動エネルギー）は存在しな

い事を間接的に証明していると解釈する事が出来る。

つまり、水中の花粉の粒子がジグザグ運動する為に必要な水分子の運動量の下限

が論理的に推定できる事と同様に、量子がジグザグ運動する為に必要な素光子の

運動量の下限を推定する事が可能と考える。

この推定値と、ゼロ点エネルギーの密度やLe Sageの重力理論に於ける重力を生じ

させるに足る宇宙の自由素光子場の密度が一致するかどうかを検討する事により

この仮定が正しいか否かの判定が可能となると考える。

　

シュレーディンガーの波動力学とハイゼンベルクの行列力学とは数学的に等価で

ある事がシュレーディンガー等により証明されたが、これが電子の運動の道筋を

表す解を欠如しているにも拘わらず、実験結果と高精度に定量的に一致した為に、

シュレーディンガー方程式を量子力学の完成された究極の基礎方程式と解釈して

いる現行の量子力学の主流派の考えでは、量子の軌道が求められない事から量子

は観測される迄は全ての可能性の不確定な重ね合わせの状態であり、観測されて

初めて波束の収縮が生じて一つの状態に収束して確定するとする大変奇妙な解釈

が生じる事を矛盾と考えたシュレーディンガーは、シュレーディンガーの猫とい

う身近な思考実験で痛烈に批判して今日まで延々と終わりのない議論が続いて来

ているが、確率過程論はこの議論に終止符を打つ事が可能な有望な理論と考える。

確率過程論から窺い知る事は、本来、自然現象という具象的な対象を研究すべき

物理学の研究者は、理論の構築の際に抽象的な高等数学で定式化した段階で十分

満足しているが、一方の数学者は、自然現象を物理学者以上に具象的に説明しよ

うと全力を挙げて努力している様に感じられるが、これは穿った見方であろうか。

なお、他の学問でも、同様な傾向がある様に思われる。

　ところで、２００３年４月に、小澤正直博士がハイゼンベルクの不確定原理の

破れの論文を発表し、約７０年振りに量子力学の基本原理が修正を受ける可能性

が出てきたが、これが正しいとすれば、ＥＰＲ論争に於けるアインシュタイン等

の主張を悉く門前払いとしてきたボーア陣営の反論の拠り所である不確定原理の

不等式が正しくない事になって反論の根拠を失う事となり、ＥＰＲ論文の正当性

が再評価される可能性がある。（巻末の文献（Ｏ））

　

（２）光子や電子等の量子の粒子性と波動性の二重性（相補性原理）

光子や電子が粒子性と波動性という相反する性質を持ち合わせている事が実験に

より確認された事が量子力学の出発点なり、波動関数という量子の状態ベクトル

の重ね合わせという理論に発展する事となった。

素粒子は、運動中には波動の性質を表し、物質との相互作用により粒子の性質が

現れる（波束の収縮、波動関数の収縮）という解釈が行われているが、波動関数

がどの段階で収縮するのかという厄介な問題（観測問題）が生じる事となった。

そこで、人が観測した時点で波動関数が収縮するという奇妙な解釈が主流となっ

ているが、シュレーディンガーの猫のパラドックス（観測されるまでは、生と死

の奇妙な重ね合わせの状態）を生む原因ともなっている。

素光子説では、素粒子と考えられている物質全てが素量子の集合体と考えるので、

波動の性質は素量子の集団による二次的な統計力学的な現象という解釈が出来る。

つまり、全ての素粒子は、粒子性という基本的な性質を持つ素量子が複数個集合

し、空間のある限局した領域を占める事によって波動性という性質が獲得されて

いる訳であり、そもそも、量子力学が説明する様な質点である電子が運動中は、

波動の性質として無限の空間に広がった波が、他の素粒子との相互作用時に波動

の性質から粒子の性質に波動関数が収縮するという様な奇妙な過程の設定も不要

のものとなると考える。

　

（３）ヤングの二重スリットの実験での単一の素粒子による干渉縞の現象

量子力学では、１個の素粒子の波動関数が同時に２つのスリットを通過して干渉

を起こし、干渉縞を生じると解釈されているが、更に、多世界解釈という新手の

到底受け入れ難い解釈も行われている。

一方、素光子説では、単一の素粒子が１つのスリットを通過する際に回折を生じ

ると同時に、宇宙空間に均等に分布している自由素光子が片方のスリットで回折

を生じ、これらが干渉を起こす結果、干渉縞を生じる（アハラノフ・ボーム効果

に於ける電子の位相の変位と同等の効果）という解釈が出来る。

これは、ドイッチェの影の光子の考えと似ているが、勿論、この様な機構を仮定

する必要は無い。

更に、最近では、フラーレン（炭素原子が６０個結合して、サッカー・ボールの

様な球体の分子）も単一で干渉縞を生じる事が実験により確認されているとの事

である。

どの程度迄の質量を持った物質がこの様な干渉縞を生じる事が出来るかに依って、

自由素光子場（近傍の電磁場としての半束縛状態の素光子の除外が必要）の密度

が推定される事になると考える。

ここで、スリットを通過する際の回折現象について考えると、波の性質の特徴で

あると解釈されているが、我々がマクロの現象としての日常的に経験する水波や

音波の回折現象の本質は、波を構成している水分子や空気中の窒素や酸素分子の

相互運動により生じる事を考えると、波特有の特徴と解釈されている回折現象も

本質的には波を構成している要素間の相互作用により生じているという事が分

かる。

また、波のもう一つの固有の性質としての干渉現象も、波を構成している要素間

の相互作用により生じているという事が分かる。

従って、粒子は回折現象や干渉現象を生じる事はないという思い込みは間違いと

言わざるを得ないし、量子が回折現象や干渉現象を生じる実験事実により、量子

は粒子の性質と波の性質の両方を併せ持っているとの解説は、間違いでは無いが、

間違った基本概念を基にした考えであり、量子についての誤った概念を植え付け

ている事になる。

ところで、素光子を含めて或る限界の質量以下の全ての粒子がスリットを通過す

る際に回折現象を生じる本質的な機序については、これ迄に解明されていないが、

素光子説に依る電磁気現象を考察した際に、物質中を通過する光の速度が低下し

たり物質の境界面における屈折や反射の現象等は全て通過している近傍の原子内

の重力の約１０^42倍の力を生じる電磁気力の源である電磁場による重力場レンズ

効果と同様な作用により光が相互作用を受ける（電磁場レンズ効果）為であると

考えると、小さな径のスリットを通過する程、回折効果が増加するという事実も

合わせると、粒子がスリットを通過する際に、スリットの辺縁部を構成している

原子内の電磁場のレンズ効果により粒子の運動方向に変化が生じるという解釈が

可能と考える。

　尚、多少飛躍するが、スリットによる素光子の回折現象を利用する事によって、

宇宙空間に存在する膨大な数の自由素光子を、利用可能なエネルギーとして取り

出す事が出来るかもしれない。（宇宙のフリー・エネルギーの利用）

これを実現するには、太陽光をレンズで集めてエネルギー密度を高める様な方法

で、スリットを通る事により不均一な分布となった自由素光子場の僅かな密度差

を増幅（集積）する方法（スリットの数と各スリット間の位置関係が基本）を作

り出す必要がある。

　

（４）場の理論に於ける数学上の抽象的な調和振動子の概念の課題

ニュートンの重力理論に於ける重力の遠隔作用が特殊相対性理論に反するという

事で、力の近接作用を説明する概念として電磁場等の場の理論が考えられて久し

いが、電磁場の本態としてその存在が実証されているベクトル・ポテンシャル

（ゲージ場）を全ての場の基本として、数学上の抽象的な概念である空間に無数

に存在していると仮定している調和振動子をゲージ場とする現在の場の量子論の

概念は、それが余りにも実験事実と合致し、完璧な理論体系である事に只々驚嘆

する余り、場の実体を更に追求する意欲をも萎えさせてしまった様に感じられる。

ここで、素光子の集団（素光子場）をゲージ場と仮定すれば、素粒子の量子化の

際に生じるエネルギーの発散の問題も生じない事となるし、そもそも、量子化と

いう一連の過程も不必要なものとなると考える。

　

尚、ベクトル・ポテンシャルの渦を巻く回転運動を回転面の方向から観察すると、

ベクトル・ポテンシャルの運動が単振動（調和振動子の運動）と同一の運動とし

て観測される事から、仮想の調和振動子の仮定が的を射たものであると考える。

アインシュタインの重力理論に於ける重力の量子化が発散の困難に直面して久し

いが、最近、その打開策として登場してきたループ量子重力理論の考えの核心は、

空間をプランク長という最小の単位で構成する事により、空間の連続性に起因す

る重力の量子化に於けるエネルギーの発散を阻止する狙いであるが、この考え方

は、自然界がアナログでは無くデジタルの要素で構成されているという考えであ

り、この考えの方向性は正しいが、肝心のエネルギーの連続性の概念の呪縛から

解放される迄には至っていない事は、誠に残念である。

　

カシミール効果やUnruh効果にてその存在が実証されているゼロ点エネルギーを、

宇宙に均等に分布して自由に光速で運動している素光子（自由素光子場）の効果

と考えると、量子力学特有の量子の不思議な振る舞いは、量子の加速度運動時に

自由素光子場から抵抗力（慣性力）を受ける事により生じる二次的な現象では無

いかと推測される。

つまり、量子固有の基本的な性質と考えられている現象も、古典的な描像の粒子

が素光子場から受ける力により生じる二次的な現象ではないかという事になる。

カシミール効果は、２つの板を至近距離に近づけると相互の板を近づける方向に

力が生じる現象であり、周囲に存在する光で、その波長が板の間の距離より長い

光は板の間に進入できずにブロックされる結果、その分だけ板の間のエネルギー

密度が減少し、その光圧差にて力（合力）が働くという事が考えられているが、

この機序は、正にLe Sageの重力理論の機序と同等であると考える。

また、Unruh効果は、真空中で光の検出器を振動させると、その振動数に一致する

光を検出器が検出するという不思議な現象であるが、検出器に固定された系で考

えると、検出器を振動させる事は、周囲の素光子場を掻き乱す事を意味し、その

結果、検出器の加速方向からの素光子場の圧力（慣性力）を受けることとなり、

これが検出器の振動周期に一致して生じる事は、つまり素光子の集団である光を

検出している状態と等しいという事になる。

　

（５）量子論に於ける仮想光子という概念の必要性

電磁気現象は、この原因粒子である光子を電子や陽子等の荷電粒子間でやり取り

する現象として説明されているが、実際に光子のやり取りが観測されている訳で

は無く、仮想の光子がその役割を果たしているとの苦しい説明が行われている。

つまり、ベクトル・ポテンシャルを物質という範疇に含まず、電子の位相を変化

させるエネルギーや運動量を持った何らかの実態であるという極めて曖昧な解釈

を続けてきているツケを負わされているものと考える。

一方、素光子説では、荷電粒子に捕捉されてその周囲を公転している半束縛状態

の素光子が定義は異なるが本質的にはベクトル・ポテンシャルそのものであり、

電磁気現象を生じさせている原因粒子であると考えているので、無理矢理に光子

を充てて辻褄を合わせる為の仮想光子の概念などの必要性は生じない。

　

（６）超弦理論に於けるユニークな多次元の概念

従来の質点の持つ無限大の発散の弱点を補うために、全ての素粒子を単一の基本

粒子(長さを持ったひも)で説明しようとする究極の統一理論として注目されてい

る超弦理論は、振動のモードで全ての素粒子の性質を表現する為のパラメーター

の自由度の不足を、次元を増やす事で補おうとする大変奇抜な考えを持った理論

である。

一方、素光子説も、素光子という単一の基本粒子で全ての物質及び物理現象を説

明しようと言う試みであり、超弦理論と競合する考えであるが、現行の素粒子と

考えられている物質は、全て束縛状態の素光子の集合体という基本概念であり、

超弦理論の様なパラメータの自由度の不足という問題も生じる事も無く、次元を

拡張する様な自然の基本的な概念を変更するトリッキーな操作の必要も生じない。

更には、素光子説は、現行のどの様な統一理論よりも、全ての現象をより単純で

統一的に説明出来る理論との自負があるが、今後のクリアーすべき終わりの無い

基本的な最後の課題として、果たして、素光子という単一の粒子のみで森羅万象

を全て表現できるのかという終わりの無い素朴な疑問だけとなる事を期待する。

　

E節＞物質観のコペルニクス的転回

ここで、少し哲学的な事柄について述べさせて頂く。

天動説に対しコペルニクスの地動説という劇的な逆転の発想は、コペルニクス的

転回として、逆転の発想の典型例として、今日でも広く引用される諺である。

我々は、物質という安定して静的な状態のものを中心に自然現象を考えることに

慣れ親しんでいる為に、陽子と中性子の結合状態や中性子の自然崩壊には何らか

の新しい力の介在が必要という考え方を持つ事は、ごく自然な成り行きと考える。

一方、素光子説は、定常状態が自然界の最高速度ｃで運動している光（素光子）

を中心に全ての現象が成り立っていると考え、素光子の集団が束縛状態となり、

最早、光速では運動出来ない集合体を形成している状態が、質量を有する全ての

物質と仮定している為に、陽子と中性子の結合状態や中性子の自然崩壊、更には

重力についても、別に新しい力を想定する必要も無く、束縛状態にある素光子で

ある素量子が基本的に保持している定常状態である光速ｃでの運動状態に復帰し

ようとする復元力により、十分説明が可能であろうとの立場にある。

従って、森羅万象を理解する為の見地として、物質中心の従来の物理学の考え方

に対し、光を中心とする素光子説の考えは、最も典型的なコペルニクス的転回と

言っても過言ではないと考える。

　

E節＞Le Sage（ル・サージュ）の重力理論の新しい解釈

　ここで、内山龍雄博士が説く、一般相対性論に於ける微分幾何学で用いられる

計量と、接続場の代わりに４脚場（フィアバイン、テトラード）とスピン接続を

時空構造として採用する事で、一般相対性理論を再構築することが出来る事とな

り、一般相対性理論をゲージ理論に統一することが可能となるとの事である。

ここで、重力場をゲージ場に統一する試みの一環として、全く別の角度から一つ

の具体的なモデルを提示する事とする。

ニュートンの万有引力の法則の発見とほぼ時を同じくして、ガリレイと共に宗教

の弾圧を恐れて秘密裏に地動説を唱えていたデカルトが、宇宙空間に充満してい

る微粒子の渦状の運動（何と、ベクトル・ポテンシャルの描像に類似）が天体の

運動を生じさせている原因と考える渦動説に基づき、地上の高いところの物体が

落下する原因は充満している微粒子（エーテル）の圧力に依るとの説を唱えて、

万有引力という遠隔作用の力の不合理性を非難して最初は多くの支持者を集めた

ものの具体的な理論の定式化や検証実験が行われなかった為に、万有引力の法則

の方程式が天体の運行（ケプラーの法則）を的確に予言する事が出来た事により、

デカルトの渦動説が次第に顧みられ無くなった事実は、物理学の発展を願う者と

して大変残念ではあるが、微粒子による渦動説と自由素光子場の概念との類似性

を考えると、大変驚嘆すべき先見性と言えよう。

なお、ニュートンの名誉の為に一言申し添えておくと、ニュートンも友人に宛て

た手紙の中で、遠隔作用を信じる人は誰もいないであろうと述べているが、重力

の作用機序を敢えて示せなかったというだけの事であり、本当に遠隔作用を信じ

ていた訳ではないと解釈すべきと考える。

　

また、自然の仕組みを突き詰めていけば、最後に究極の単純な要素に辿り着く筈

であろうというデカルトの還元主義の自然観は、同時代のライプニッツのモナド

の概念と一致しており、今日に於いても最も強力な指導原理であり、全ての自然

科学者の強い研究意欲と実り多い研究成果への期待感を抱き続ける為の心の支え

になっている事も事実であろう。

余談であるが、還元論に対する批判として、下部構造を仮定するとその構成要素

についてもその下部構造を仮定する事が必要となり、終わりのない底なし沼に填

り込んでしまうという感想をよく聞くが、底なし沼に身を挺して果敢に挑戦する

事こそ、多くの実りを得ることが可能になると考える。

その後、１６９０年にスイス人の数学者であるNicolas Fatioがデカルトの渦動説

を発展させて、宇宙空間に充満する微粒子の存在を仮定すると、物質によるその

運動の遮蔽効果により引力が生じるという説を唱え、更にこれを発展する形で、

１７５８年にジュネーブ人のLe Sage（ル・サージュ）が重力発生のメカニズムを

論文；"Lucrèce Newtonien"（ニュートン的ルクレティウス）として発表している。

（巻末の参考文献（Ｆ）を参照）

この核心は、宇宙空間に微粒子の存在を仮定するだけで、２つの物体間に、物体

の質量の積及び物体間の距離の逆二乗に比例する引力が生じるという単純明快な

万有引力の発生機序を、ル・サージュが初めて気付いたという事である。

この重力理論は、１９世紀末のケルビンやマクスウェルらの著名な物理学者達に

も注目されて論じられていた（参考文献Ｆ）が、１９１６年にアインシュタイン

の一般相対性理論が発表されて、その解としての予言の全てが天体観測により悉

く実証されるに及んで、次第に研究の対象から消え去っていった。

　

　ファインマンが、１９６４年にコーネル大学で一般向けの講演会を行った時に、

間違った理論の代表例として、Le Sageの重力理論を採り上げ、宇宙空間を運動中

の天体は、進行方向から天体に衝突する微粒子の頻度が逆方向から衝突する頻度

を上回る事で抵抗を受けて減速し、何れは宇宙のある慣性系に静止した状態にな

る事が予想されるが、天体の観測の結果では、この様な現象を観測していない事

から、この理論は間違っていると結論付けている。

この講演記録は、ファインマンの啓蒙書（巻末の文献(Ｆ)を参照）に記載されて

いるが、このガス状の微粒子の集団（フェルミオン）を素光子場（ボソン）とす

る事により、ファインマンの指摘は該当しない様になると考えている。

余談ではあるが、ファインマンともあろう当時のトップの物理学者がこの微粒子

を光子という質量がゼロの素粒子と仮定した場合に、自ら指摘した矛盾が解消す

る可能性に何故気付かなかったのか、些か不可解ではある。

更に、Le Sageの重力理論に関し、下記の主な疑問点（参考文献（Ｆ）の（１））

等が指摘されているので、私見を述べる。

　

疑問１；粒子の流れの掩蔽が起こるためには、粒子を物体がいくらか吸収しなけ

ればならないことで、これは物体の温度の上昇を伴うと考えられる。

回答１；素光子は物質と完全弾性衝突すると考えるが、一部が物質に吸収される

機会が存在する事は否定できないが、或る閾値に達するとエネルギー的に不安定

の状態となり、安定な状態へ戻る過程で吸収された素光子を放出する事が想定さ

れる事となり、物質の温度が上昇する現象は生じないと考える。

　

疑問２；運動する物体間の重力を説明するためには粒子の速度は光速をこえなけ

ればならない。

回答２；素光子という光速で常に運動している粒子を想定する事で、矛盾は生じ

ないものと考える。

　

疑問３；粒子の速度を高速だと仮定すると吸収による温度の上昇はさらに上昇し

なければならない。

回答３；回答１の様に、光速で運動している素光子の衝突で物質の温度の上昇は

生じないものと考えられる。

　

疑問４；物質による素光子の運動の遮蔽効果があるにせよ、遮蔽されて散乱した

素光子の数と貫通した素光子の数を合計すると物体間の素光子の総数は不変とな

り、物体間の自由素光子場の密度が低下する事は無いのではないか？

回答４；自由素光子場に在る１つの物体は周囲の素光子が均等に貫通や衝突して

散乱する事で、この物体の周囲の自由素光子場の密度に変化は生じない事となる

が、散乱した素光子の方向が散乱後に変化することで、密度の変化は生じなくと

も、ベクトルとしての密度の分布に変化が生じることが予想される。

この物体の近くに別の物体が存在した場合には、各々の物体の周囲の素光子場の

密度は均等で等しい為に、一見すると、２つの物体間の素光子場の密度も低下す

ることが無い様に思われる。

そこで、簡単の為に、初期条件として物体間の距離がゼロ（物体間には素光子が

存在しない）の場合を考えてみる。

更に、２つの物体は素光子の遮蔽率が１００％という極限の状態を想定してみる

と、周囲の素光子が２つの物体に均等に衝突する事で、物体間にお互いを引き付

け合う方向に合力が働くことになるが、この状態は大気圧で物体に吸着している

吸盤の状態に例えられる。

次に、この状態の２つの物体に働いている引力と同じ力で２つの物体を引き離し

た場合にも、矢張り、物体間の物体方向の素光子の密度はゼロの状態を保ってい

る事となる。

そこで、この状態で、２つの物体の素光子の遮蔽率が１００％より低下している

場合には、物体で遮蔽された分の素光子を差し引いて低下した密度の素光子場が

物体間の物体方向に生じる事となり、物体間の素光子場の密度の低下に起因する

合力が２つの物体を近づける方向に働く事となる。

　

　ところで、実際の重力効果を満足させるに足る力を生じる事が可能かどうかは、

宇宙空間に存在する自由素光子の密度の分布（自由素光子場）を測定することに

より、この考えの正否の決着が可能であるが、ゼロ点エネルギーの密度を定量的

に求める事（例えば、カシミール効果にて）で達成可能と考える。

この一例として、自由素光子場と同一と考える零点エネルギーの論理的な上限の

密度が、巻末の文献の（Ｘ）の（１）によれば、質量密度で１０^94g/cm^3と非常

に大きな値を持っている事が導出されている。

更に、この様な高密度のエネルギー場を慣性運動している物体が、運動方向から

のエネルギーによる抵抗を受けないという事実も、これまでの全ての観測結果か

らも実証されている事を考えると、ファインマンが指摘したLe Sageの重力理論の

最大の懸案事項は解決したものと考える。

尤も、素光子場の密度を導出するまでも無く、現に、宇宙空間を飛び交っている

2.7Kのマイクロ波の宇宙背景放射や全天体から放出されている様々な波長の光や、

更に全ての原子から宇宙空間に漏れ出している電場等の存在を考えると、少なく

ともLe Sageの重力理論の効果を全く考慮していない現行の全ての重力理論に於い

て、何らかの補正作業を必要としている事は明白であろう。

　

Le Sageの重力理論の中核となる遮蔽効果は、直観的には距離の逆二乗則(ｒ^-2)

に従う引力が働く様に考えられるが、ｒ^-ｎの形式で、微生物より小さいミクロ

のスケールの距離に於いてはｎ＞２、太陽系程度までのスケールの距離に於いて

はｎ≒２、銀河程度のスケールの距離に於いてはｎ≒１、更に銀河団以上の大き

いスケールの距離ではｎ≒０（減衰しない平行光線と同様な性質）となる様に、

距離ｒが増加するに従い係数ｎが減少するのではないかと推測している。

この推測が当たるか否かの判定は、銀河内の恒星の運動をドップラー効果で推測

した様な手段により、銀河の直径よりも長い距離に位置する銀河団や超銀河団の

運動を、光のドップラー効果を観測する事で間接的に推測する事で可能となるの

ではないかと考える。

つまり、宇宙の大規模構造の縦方向の運動を専ら観測しているが、同距離にある

大規模構造間の横方向の運動を観測する事が、これから重要になると考える。

なお、この結果、遠くの天体の赤方偏移が宇宙の膨張により生じている（宇宙論

的赤方偏移）か否かの判定が可能となるかも知れない。

　

物体に依る自由素光子の運動の遮蔽効果が距離の要素としてのｒ^(-ｎ(r))の形式

に於ける距離ｒの拡大に伴い、距離ｒに依存して変化する（距離を因子に持つ）

冪数ｎ(r)が、ミクロからマクロ,果ては、宇宙規模の距離の拡大に伴い連続的に

２以上⇒２⇒１⇒０へと連続的に減少する可能性が考えられる。

　

以上の根拠を述べる。

分子間には距離の６乗に逆比例する「ファンデルワールス力」という引力が生じ

るが、「カシミール効果」は２つの微小な平板間に距離の４乗に逆比例した引力

が生じる事となる。

勿論、重力が逆二乗則に従う事を前提としている一般相対性理論では、この様な

力は距離の逆二乗則に従わない為に、重力以外の原因として説明されている事に

なっている。

なお、電磁気現象のクーロン力は、厳密に距離の逆二乗則に従うことが論理的に

且つ実験的に確かめられているが、重力の作用機序が確定していない現状では、

距離の逆二乗則に従う事が絶対条件でなければならない理由は無い。

尤も、一般相対性理論の重力場方程式では、質量（エネルギー）を重力源として

二次的な空間の歪みを重力の発生原因としているので、電荷を電磁気力の原因と

考えているクーロン力と同様に、距離の逆二乗則に従う事が厳密に導かれている。

　

銀河の周囲を回転している恒星の速度が、銀河の中心から遠くに位置する場合で

もその回転速度が低下せず、恰も一塊となった円盤様の運動の謎に対し、観測に

掛らない物質（暗黒物質）の存在を仮定して説明しようとする考えが主流の理論

であるが、１９８３年に、イスラエルの物理学者であるモンデハイ・ミルグロム

が、銀河スケールではニュートンの万有引力の法則を修正する距離の逆数に従う

引力が生じるとするＭＯＮＤ（Modified Newtonian Dynamics）を発表して、暗黒

物質の存在の仮定の必要性が無い事を説いたが、その後宇宙探査機のパイオニア

が太陽圏を脱出する際に予測を上回る太陽からの引力を観測した事で、この理論

が注目されている。

下記の文章は、参考文献（Ｗ）の（５）の抜粋部分を改変したものである。

　

　ＭＯＮＤは、ニュートンの運動方程式 (運動の第２法則) F=ma への修正として

記述され、これを、F=ｍμ(ａ/ａ0)*ａと変更する。

　ただし、μ(x) はある関数であり、その具体的な表式は与えられていないが、

x ≫ 1 のとき μ(x)≒1, x ≪ 1 で μ(x)≒x であることを要請する。

また、a0 はある基本的物理定数となるものであり、極めて小さな値をもつと想定

される。

主として検討されるのは重力の相互作用のみである。

惑星が太陽によって受けている加速度と、太陽が銀河公転で受けている加速度と

の間には 1 万倍以上の開きがあるため、ＭＯＮＤでは日常の現象と銀河の現象と

では μ による効果がまったく異なるものだとする。

すなわち、太陽系内を含む日常のスケールでは、ａ0よりもａがはるかに大きく

μ(x)≒1 とみなされる。

この場合、ニュートン力学との違いは表れない。

　一方、恒星間や銀河、銀河間のスケールでは ａがａ0に近いかそれを下回り、

μ(x)＝x, すなわち力が加速度の二乗に比例するような影響が無視し得ない。

このＭＯＮＤから銀河回転の説明を行うのは容易である。

ニュートンの万有引力 F＝GMm/r^2 による相互作用を考えるだけならば、ａ0より

もａが十分小さい (x ≪ 1) 場合には、この変更から二体問題の運動方程式ａ＝

√(ＧＭａ0/r)が直ちに得られる (但し、ａは加速度、ＧＭは万有引力定数と作用

を及ぼす物体の質量の積ｒは両者の距離)。

　中心力を受けて速度ｖで等速円運動する天体を考えると、一般にａ＝ｖ^2/ｒが

成立するので、速度はｖ＝(ＧＭａ0)^1/4となり、これは距離 r によらない定数

である。 すなわち重力の及ぼす加速度が距離に反比例するなら回転の速度は距離

によらず一定であることが自然に導かれ、少なくとも銀河の中心から遠く、銀河

を質点とみなす近似が成り立つ元で回転の観測事実の簡明な説明を与える。

逆にこの表式からａ0を推定することが出来る事になり、ミルグロムによれば、

ａ0 =1.2 × 10-10 m/s2 である。

　1998年以降、銀河の観測とは別の方向から、より直接にＭＯＮＤ説を強化する

証拠と成り得る観測事実が報告された。

太陽系から初めて脱出する事になった惑星探査機パイオニア10号と11号の速度が

予測よりも有意に減少していることが報告され、太陽に向かった未知の力が働い

ているものとして解釈できることが示された。

この現象はパイオニア・アノマリーと呼ばれ、その原因が様々に議論されている

が現在もなお未解明である。

もし ＭＯＮＤが主張する様に、相互作用が非常に弱い場合、重力が従来信じられ

ていたものよりも相対的に強いとすれば、それはパイオニア・アノマリーに対す

るひとつの説明となる。

一方で、遠方の銀河が起こす重力レンズの観測からは、推定された銀河の質量を

用いて一般相対論で予測された効果よりも大きな曲がりが検出されており、これ

は暗黒物質の存在を示唆している。

ＭＯＮＤそのものは相対論的現象を扱えないので、重力レンズの説明に関しては

無力である。（引用終わり）

　

これまで述べた様々な現象を、Le Sageの重力理論のみで説明できる可能性が大い

にあると考える。

本来は、Le Sageの重力理論の中核の概念である物体による自由素光子の光速での

運動の遮蔽効果を定式化して定量的に評価する事で推論の是非を判定する必要が

あるが、以下に、これまでの推論を基にして、Le Sageの重力方程式の概略を推測

する。

　

２つの物体の質量を各々Ｍ、ｍとし、物体間の距離をｒとする。

物体の遮蔽率Ｂは物体の質量に比例する事となるので、Ｂは質量の関数となり、

それぞれの遮蔽率をＢ（Ｍ）、Ｂ（ｍ）とすると、物体間の自由素光子場の密度

の減少率Ｄは、各々の物体に密度及び物体間の距離ｒにより決定される事が推測

される。

距離ｒを因子とする重力の減衰率を表す関数Ｒは、これまでの推測により、

　

Ｒ（ｒ）＝ｒ^(-ｎ(r))　（０≦ｎ(r)≦α）

　

を推測している。

ここで、αは原子核以下のミクロのスケール（最低がプランク長？）での距離の

要素に付加すべき距離のべき数であり、理論値として導出して実験結果にて確定

されるものである。

そこで、物体間の自由素光子場の密度の減少率Ｄ（Ｍ、ｍ、ｒ）は、

　

Ｄ（Ｍ，ｍ、ｒ）＝Ｂ（Ｍ）・Ｂ（ｍ）・Ｒ（ｒ）

　

という２つの物体の遮蔽率の積及び距離に関する重力の減衰関数の積で表される

事となるものと推測する。

但し、物体を透過せずに物体に衝突して散乱する素光子に依り、他方の物体に及

ぼす素光子場の密度が増加する事となり、お互いの物体に衝突して物体間の距離

が遠ざかる方向に働く斥力Ｆｒ（Ｍ，ｍ、ｒ）が増加する事も推測される事とな

り、この効果を加味する事が必要であり、この斥力Ｆｒを定式化する必要がある。

以上の考察により、距離ｒ離れた質量がＭ及びｍの２つの物体を近づける方向に

働く力Ｆは、宇宙空間の零点エネルギーの質量密度をρ、ｋを比例定数として、

　

Ｆ＝ｋ・ρ・Ｄ（Ｍ，ｍ、ｒ）−Ｆｒ（ρ、Ｍ，ｍ、ｒ）

　

という形式で表される事が予想される。

なお、引力Ｆは物体による零点エネルギー（自由素光子場）の遮蔽率が１００％

の状態に於ける重力を最大の引力である極限値として、非線形に変化して頭打ち

状態になる事が予想される。（重力の非線形性）

その結果、Le Sageの重力理論に於いては、光も脱出不可能なブラック・ホールは

論理的に生じない事が導かれる。

また、零点エネルギーの質量密度の論理的な上限値が約５×１０^94g/cm^3と非常

に高密度である事による、このエネルギーの吸収によるブラック・ホールの急速

な肥大化やこのエネルギーの宇宙定数への多大な関与等の一般相対性理論に関す

る重大な問題も生じない事となる。

以上が、Le Sageの重力方程式の推定式である。

現在の急務は、Le Sageの重力理論の遮蔽効果を厳密に定式化して、重力場方程式

の厳密解を完成させる事である。

　

E節＞ル・サージュの重力理論と一般相対性理論の相違点

ここで、一般相対性理論（相対論）とLe Sageの重力理論（ＬＴＧ）の違いについ

て、私見を列記する。

　

（１）重力の発生機序

相対論；物体の質量（エネルギー）の効果として、物体の周囲に時空の歪みが生

じ、この歪んだ時空が及ぼす物体の振る舞いが、恰も重力を生じている様に観測

されるという大変ユニークなアインシュタインならではの解釈である。

但し、ゴムマット上に鉄の玉を載せた場合に、マットが重力で沈み込む事で時空

の歪みを視覚的に理解させる努力が行われているが、質量（エネルギー）が時空

を歪ませる機序については全く説明されていない訳であり、アインシュタインの

天才的な閃きにて課題を置き換えたに過ぎず、肝心の重力の発生機序を説明した

事にはならない。

なお、重力は２つの物体間の距離の２乗に逆比例する（距離の逆２乗則）という

概念がニュートンの万有引力の法則から継承されている形になっている。

これはクーロン力の距離の逆２乗則との共通点であり、電磁気力と重力の類似点

を考察する際の最も大きな拠り所となっている。

ところで、零点エネルギーの密度が、巻末の文献の（Ｘ）の（１）によれば質量

密度で１０^94g/cm^3と非常に大きな値を持っている事が導出されている事を考え

ると、零点エネルギーの存在だけで宇宙空間が大きく歪む事となり、宇宙現象の

観測事実からはこれを示唆する現象は認められていないという大きな問題を内存

している。

重力の伝播速度は論理的に光速ｃに等しいという解が導かれているが、これは、

時空の歪みという幾何学的構造の変化が伝達される速度を意味する事となるが、

古い概念のエーテルを媒質とする光の伝播の考えに似た困難に直面せざるを得な

い様に思える。

更に、時空の歪み（幾何学的な変化）の概念は、無意識の内に絶対空間の概念を

内存している事にもなると考える。

　

ＬＴＧ；宇宙空間に均等に分布し光速で飛び交う自由素光子の存在を仮定すると、

物体による素光子の運動を遮断する遮蔽効果により、お互いの物体が近づく方向

に素光子の衝突（素光子圧）による合力が働く。

なお、その合力は、大ざっぱには２つの物体の質量（素光子の遮蔽効果に比例）

の積に比例し、２つの物体の間の距離の２乗に逆比例するというものである。

但し、２つの物体の質量の積に線形に比例する訳ではなく、物体の質量に依存す

る遮蔽効果の割合により重力が決定される事となる為に、厳密には非線形に比例

する事となり、宇宙空間に存在する素光子の密度に依存して重力の上限が決定さ

れる事となり、光すら脱出不可能なブラックホールが形成される事は無い。

更に、重力が距離の逆２乗則に従うという事も、前に述べた様に、細胞レベルの

スケールから太陽系のスケールまでに限定された近似的な法則という事になる。

なお、物体による自由素光子の運動の遮蔽効果により生じる２つの物体間の自由

素光子場の密度分布の変化と相対論の空間の歪みを比較検討する事により、その

本質的な違いを見出すことが出来るかも知れない。

ところで、重力の本態が素光子場という観点から、任意の慣性系に於ける重力の

伝播速度が光の伝播速度ｃに等しいことが容易に導かれるが、相対性原理が要請

する任意の慣性系に於ける重力現象が等しく発現する事を保証する結果となる。

なお、慣性系に於ける重力現象とはどの様な状態を想定しているのかという疑問

に対しては、今後の厳密な検討課題としたいが、一般相対性原理に代わる任意の

慣性系のみならず非慣性系で成立する新しい相対性原理を確立する作業としたい。

　

（２）ブラック・ホール

相対論；物体の質量（エネルギー）の増大に比例して、重力が増加する事となり、

光さえも天井知らずの強大な重力場に捕捉されて脱出できない、所謂、ブラック

・ホールの存在が論理的に予言されている。

また、宇宙の観測の結果、ブラック・ホールの性質に該当すると思われる天体も

発見されている。

　

ＬＴＧ；重力の発生機序から明かな様に、自由素光子場の密度が重力の最大値を

決定するので、重力が２つの物体の質量の積に比例する状態で増加するが、最大

値に近づくに連れて、頭打ちの状態になると考えられる。

つまり、重力は、質量の積に線形性に増加する訳では無く、非線形性に増加し、

論理的な最大値（極大値）に近づくに連れて頭打ち状態になると予想される。

従って、重力方程式の係数はニュートンの万有引力の方程式の係数の重力定数Ｇ

とは異なり、質量に依存して非線形に変化する変数を取る事となると考える。

また、重力が最大値を取る場合は、確かに物体により素光子の全てが完全に遮断

される結果、透過する素光子（その集団である光も含めて）は皆無となり、この

現象を光すら脱出出来ないという見方も出来ない訳では無いが、宇宙空間に存在

する自由素光子場からの抵抗により素光子が空間を運動できない状態になる訳で

は無く、この巨大な質量を持った物体上の光源から光が放射される際に、放射の

方向に依り、重力レンズ効果で光が脱出出来ない場合も有り得るが、その他の光

は物体から宇宙空間に放射される事が予測される。

従って、ブラック・ホールの存在は論理的に否定される。

なお、ブラック・ホールに関する疑問で、宇宙空間に存在するゼロ点エネルギー

がブラック・ホールに吸い込まれ続けると宇宙が比較的安定した状態を保つこと

は出来なくなると考えるが、下記の宇宙定数に関するゼロ点エネルギーに関する

未解決問題も有る。（巻末の（Ｘ）の（１）の「宇宙定数問題」を参照）

また、巻末の（Ｘ）の（２）のウロボロスの蛇の様に、宇宙の構成要素としての

ブラック・ホールに宇宙自体が飲み込まれてしまう様な矛盾も生じるかも知れな

い。

　

（３）慣性系と加速度系の解釈（地上を例として）

相対論；重力と慣性力の等価性（この２つの力の違いを区別出来ない）が、この

理論の最大の前提となっているので、見かけの力と考えられている慣性力に対応

し、重力も見かけの力と解釈している。

更に、重力を見かけの力と見なすことに依り、重力の発生機序としての質量によ

る空間の歪みとする仮定を何の支障もなく受け入れることが可能となる。

アインシュタインは、自由落下による無重量状態を（局所的）慣性系と解釈して

等価原理を思い付いたと言われている。

また、重力場にて光の進行が曲げられる重力レンズ効果があるが、エレベータ内

で自由落下中の観測装置は、光も観測装置と一緒に自由落下している事により、

光が曲がる運動が相殺されて、光が直線的に運動している事を観測する事となり、

自由落下状態が加速度運動では無く、慣性運動である事を示唆する現象である。

但し、これはあくまで局所的な無重力の現象であり、これをもって慣性系と解釈

する事には可成りの抵抗を感じざるを得ない。

つまり、エレベータに窓が開いていて天体を観測する事が出来れば、加速度運動

を行っている事が容易に判定出来る事となり、あくまでも、局所的な無重力状態

を根拠とする見かけの慣性運動状態、つまり、本質的には加速運動状態という事

になる。

　一方、地上の観測者は、作用と反作用の関係で、地面から観測者の足底部に向

けて重力という外力（作用）が常時加えられる事により加速運動状態にあるが、

観測者の足底部からこの外力と反対方向に反作用の力が地面に掛かる事により、

無重力状態には無い事となり、実際に運動状態には無いが加速度運動を行ってい

ると解釈される。

但し、客観的に観察すれば、地上の観測者は、重力で地面に常に押さえつけられ

ている状態にあり、これが作用であり、地面が観測者に与える力は抵抗力という

反作用であり、作用と反作用の因果関係が逆転した解釈と言わざるを得ない。

　

ＬＴＧ；エレベータの自由落下を地上から観測すると、エレベータは確かに加速

しながら落下している（加速度運動）状態として観測される。

これは、素光子の密度の勾配（相対論の時空の歪みの勾配に対応する）に沿って、

素光子が物質に衝突する力によりエレベータが加速度運動を行っている事になる。

なお、自由落下中の観測者は確かに無重量状態にあるが、エレベータ内の全ての

物質に一様に外力（素光子の衝突）による加速度が及んでいる結果、外力が及ん

でいない様に錯覚されるだけの事である。

この事は光も例外では無く、光の重力レンズ効果も光の自由落下に起因する現象

と考えれば、自由落下中の観測者からは、重力効果を打ち消す様な加速度運動に

より、光は直進している様に観測されるし、光の速度も慣性系での観測に準じて、

光速ｃで観測される事となる事により、加速度計や光の速度を測定して慣性運動

か加速運動かを局所的に判断する事は原理的に不可能であり、エレベータの窓を

開けて天体との相対運動を比較して判断する事になる訳であるが、つまり、この

加速度運動状態が相対論で言う局所慣性系という事になる。

ところで、自由落下する物質で加速度がゼロの場合を慣性運動状態という捉え方

も間違いでは無く、宇宙空間で慣性運動中の物質は、加速度ゼロで自由落下して

いるという表現も成立する。

なお、一般的な乗り物を推進力で加速する場合は、乗り物全体に同時に均等な力

が働く事か出来ず、推進力の伝達の遅延効果を加速状態として感じる訳であり、

加速度計や光の速度の変化を観測する事により加速度を定量的に求める事が出来

るが、自由落下の場合は他の慣性系から観察する事でしか物体の加速状態の有無

を判定する事が出来ないという事である。

　一方、地上の観測者は、確かに無重力状態には無く、素光子の密度の勾配に沿

って地面に押しけられる重力を受けているが、地面に依りその運動が阻害されて、

加速度運動が出来ない状態にあるという事であり、結局、作用と反作用の関係で、

重力と地面の抗力が釣り合って静止状態にあり、これは加速度運動を行っている

訳では無く、或る意味で外力が働かない慣性運動と解釈する事も出来ると考える。

　

なお、素光子説の立場では、後ほど詳しく考察する慣性力及び重力は見かけの力

では無く、素光子が実際に物体に及ぼす絶対的な力が原因であり、観測者の立場

で変化する様な見かけの現象とは本質的に異なると考える。

従って、現行の力学理論の考えに反し、慣性力に起因する遠心力やコリオリ力も

絶対的な力という解釈が妥当ではないかと考える。

なお、現行の考えでは、系に依存して生じたり生じなかったりする力を見かけの

力と判断している様であるが、観測する系はあくまで慣性系であるべきであり、

加速度系で観測する事を許せば、系の取り方によって、全ての力が無くなる系を

選択する事が可能となり、物理現象に於ける全ての力が見かけの力であると極論

される恐れが生じる事となり、これでは納得する事は出来ない。

　

　慣性質量と重力質量の等価性は、多くの実験により精密に検証されている事に

より、疑いのない事実と考えられている。

素光子説に於いて、宇宙空間に均等に分布している自由素光子場を想定すると、

この時点で、宇宙に基準となる慣性系を自動的に設定する事を意味する。

つまり、慣性系とは、周囲の素光子場からの圧力を均等に受けている合力ゼロの

状態の系という事であり、別の見方をすれば、全く周囲から力を及ぼされていな

い状態の系という現行の慣性系の定義と合致する。

これは、ニュートンの絶対静止系の考えとは異なるが、慣性系と加速度系の違い

を明確にする為にも、重要な設定と考える。

そこで、自由素光子の密度が均等な状態の空間に１つの物体が存在すれば、周囲

の自由素光子が均等にその物体に衝突する結果、その物体には合力ゼロ、つまり

恰も何の外力も働いていない慣性運動の状態にある事となる。

ここで、この物体に外力（半束縛状態の素光子の運動に起因する電磁気力）が加

えられると、物体が加速運動を行うが、その瞬間に自由素光子場の加速度方向か

らの素光子の速度が光速ｃから増加する結果、その分の素光子の運動量が増加し、

　一方、逆方向からの素光子の速度が光速ｃから減少する結果、その分の素光子

の運動量が減少し、更に素光子の密度（単位時間に物体に衝突する素光子の数）

も同様な変化を伴う結果、素光子場が物体に及ぼす合力が加速方向と反対の方向

に向かう抗力として働く事となるが、これが慣性力として観測される事となる。

つまり、慣性の法則とは、物体に外力が働かなければ等速直線運動を行うという

極当たり前の現象を述べているだけではなく、しっかりとその運動状態を保持し

ている現象（均等に自由素光子が衝突して合力零の状態）と考える事が出来るが、

その結果、物体に及ぼされた外力に抗する力としての慣性力が発現する事となる。

つまり、外力に対抗する反対方向の抗力としての慣性力が発現する現象を、作用

反作用の法則と呼んでいる事となるが、反作用としての抗力が作用としての外力

よりも力の発現が遅延する事により、物体が加速される事が可能となる。

この様に、慣性力とは、物体と素光子の衝突に起因する絶対的な力と考える。

なお、電子やニュートリノや核子を構成している素量子が安定した束縛状態を保

てる大きな要因として、周囲からの自由素光子の圧力（素光子圧と名付ける）に

依ると推測する。

　

ここで、ニュートンの運動方程式について考察する。

Ｆ（外力）＝ｍ（物体の質量）・α（物体の加速度）から、α＝Ｆ／ｍとなり、

加速度αは、外力の強さＦに比例し物体の質量に逆比例する事となる。

そこで、この質量は物体の動き難さの指標となる慣性質量の事であるが、これを

物体を構成している素量子（束縛状態の素光子）の総数の意味に考えると、外力

Ｆが物体を構成する全ての素量子に均等に分配される結果生じる全ての素量子の

加速度がαになる事を意味する事となり、ニュートンの運動方程式の意味が明確

になる。

物質が質量を有し慣性力が生じる機序として、現行の素粒子論ではヒッグス機構

を想定しているが、素光子説では不要の概念となる。

　

次に、この物体の近くに別の物体が存在している場合は、物体による自由素光子

の運動の遮蔽効果にて、２つの物体の質量の積に比例し、物体間の距離の二乗に

逆比例する形で物体間の素光子の密度が低下し、その密度差に依る合力が、恰も、

物体同士を引きつけ合う方向に働く力が生じるという考えが、Le Sageの重力理論

であるが、この質量は所謂、重さを表す重力質量の事を指すが、物体による自由

素光子の運動の遮蔽効果は物体を構成している素量子が素光子と衝突して素光子

による物体の貫通を阻止する事により達成される事を考えると、重力質量も物体

を構成している素量子の総数に比例するものと考える事が出来る。

　

以上より、慣性質量及び重力質量は共に物体を構成している素量子の総数という

物理量を意味しており、経験則に基づく等価という曖昧な表現では無く、元来は

論理的に同一の物理量を表しているものと考える事が出来る。

　ここで、質量の概念を再考すると、元来、質量とは物質に力を加えた場合の動

き難さの割合として定義されているが、これは即ち慣性質量や重力質量の事を指

している訳であるが、一方、エネルギーと質量の等価式である、Ｅ＝ｍｃ^2に現

れる質量ｍは、顕性のエネルギーとしての運動エネルギーに対比される不顕性の

エネルギーとしての質量エネルギーを表す指標という解釈が成立するとすれば、

質量の概念を拡張して考える必要があろう。

つまり、例えば、光子（素光子）の質量がゼロという場合の質量の意味合いは、

慣性質量や重力質量がゼロという意味合いではなく、不顕性エネルギーの指標と

しての質量がゼロという事であり、顕性エネルギーが全開となる運動エネルギー

が最大に発揮されている最高速度ｃでの運動状態の場合に当たる。

また、物質の運動エネルギーが観測する系（物質との相対速度）に依存して変化

することも、物質を構成している素量子の顕性エネルギー（運動エネルギー）と

不顕性エネルギー（質量エネルギー）の割合が、相対速度に応じて相補的に変化

すると考えると、エネルギーと質量の等価式の意味がより身近に実感される。

　

Ｅ節＞宇宙空間を伝播中の光の振幅の減少効果を仮定した天体までの距離の推測

　宇宙を観測する場合の天体までの距離は、セファイド�Tａ型超新星の固有の明

るさがどの場合も同じという理論的な裏付けの基、この星までの距離を基準にし

て、全ての天体の距離が算出されている。

ここで、電磁波が宇宙空間を運動中に、素光子同士の衝突が生じる可能性を考え

ると、電磁波の波の構成要素である素光子が減少し、振幅が減少する現象が予想

される事になる。

これを定量的に書くと、電磁波が宇宙空間を運動する時間をＴ、電磁波の成分で

ある１個の素光子が自由素光子と衝突して電磁波外に弾き出される単位時間当た

りの個数をＰ／ｓ（簡単のために宇宙空間の自由素光子場の密度は均一とする）

とすれば、単位時間に弾き出される１波長分の素光子の総数はその１０^８倍であ

るので、電磁波がＴ秒間運動している間に素光子同士の衝突で素光子が、

Ｐ・Ｔ・１０^8個減少する結果、電磁波の１波長の波の素光子の総数Ｎは、

　

Ｎ≒１０^8−Ｐ・Ｔ・１０^8

　＝１０^8（１−Ｐ・Ｔ）

　

となるが、天体の光源から観測者までの距離をＬとすれば、Ｌ＝Ｔ・ｃであり、

素光子１個のエネルギーがｈ／ｓであるので、

減衰した電磁波の１波長分のエネルギーは、１０^8（１−Ｐ・Ｌ／ｃ）・ｈ／ｓ

となる。

そこで、電磁波の全エネルギーの減衰率Ｓは、

　

Ｓ≒Ｎ／１０^8

　＝１０^8（１−Ｐ・Ｌ／ｃ）／１０^8

　＝１−Ｐ・Ｌ／ｃ　　・・・（１）

　

つまり、観測された天体の電磁波の全エネルギーの減衰率Ｓから、天体迄の距離

Ｌを求める事が出来る事となる。

尚、素光子同士の衝突の単位時間当たりの頻度Ｐは、自由素光子場の密度（ゼロ

点エネルギーの密度と素光子のエネルギーｈ／ｓから算出可能）と素光子の直径

（プランク長と仮定）から導出可能である。

なお、光子１個,１個を区別して観測する技術が確立されているので、天体からの

光の全エネルギーを測定し、それを構成している光子の個数を検出する事により、

１個の光子のエネルギーＥ１が導出される事となり、減衰前の光子のエネルギー

Ｅ０は、Ｅ０＝ｈνであり、減衰率Ｓは、

　

Ｓ＝Ｅ１／Ｅ０

　＝Ｅ１／ｈν　・・・（２）

　

従って、（１）と（２）より、

　

１−Ｐ・Ｌ／ｃ＝Ｅ１／ｈν

∴Ｌ＝ｃ（ｈν−Ｅ１）／（Ｐ・ｈν）

　

となり、天体までの距離Ｌを求める事が出来る。

　

ここで、目下の最大の課題は、天体の光を観測して、天体までの距離に比例して

減衰している光を果たして検出できるかという事である。

もし、この現象が確認されて、遠い天体までの距離が正確に測れる様になれは、

宇宙の仕組みの認識が変わる可能性が生まれ、更には、素光子の存在を間接的に

証明する決め手となると考える。

　

なお、天体が発する光を観測した場合は、その天体を構成している全ての元素の

電子からの放射光が混合した光という事で、光のスペクトルを分析して、光源と

静止した観測装置での標準のスペクトルとを比較する事によってトップラー効果

による赤方偏移や青方偏移の割合を調べる事により、天体と観測機器と相対速度

を導出する事が行われているが、単色光を観測する場合はスペクトルを描く事が

出来ないので、この方法で天体との相対速度を求める事は極めて困難となる。

そこで、光源と観測機器の相対速度がゼロの場合は振動数に拘わらず放射時間Ｔ

が一定という全宇宙に共通する自然現象を利用する事によって、放射時間すなわ

ち光と観測機器の相互作用時間を観測して、標準の放射時間Ｔとのずれの割合を

計算する事で光源と観測機器との相対速度を導出する事が可能となると考える。

なお、付け加えると、宇宙の物質の９５％上はプラズマ状態と言われているので、

測定した相互作用時間を基に、プラズマ状態の天体からの光であるかどうかを先

ず判定する作業が必要となる。

　

更に、天体からの光の赤方偏移は、一般的なドップラー効果だけでは無く、宇宙

の加速膨張の効果も加味されていると考えられている訳であるが、天体からの光

と観測機器との相互作用時間を測定する事で、宇宙の加速膨張の有無の判定やそ

の割合が赤方偏移以外の新しい方法で導出可能となるかも知れない。

なお、空間の膨張とはいったいどの様な物理現象を引き起こす事であるかという

事を、物理学的に定式化する事が先ず必要と考える。

　

E節＞非線形距離の概念の導入に依る有限定常宇宙論の提案

　無限大や無限小という無限の付く量は数学上の抽象的な概念であり、自然現象

という具象的な対象物を研究する物理学には馴染めない概念と考える。

直観的に、無限大に伸びている直線（線形の速度）をギューッと押し縮めて曲線

（円弧）にしたものが、光速ｃを極限値とする非線形の速度になるという描像を

描いているが、この類推として無限大に直線的に伸びている宇宙空間をギューッ

と押し縮めて非線形に増減する距離の性質を備えた空間が現在の宇宙という漠然

とした描像を描いている。

ここで、非線形の相対速度に習って、非線形の相対距離なる概念を仮定してみる。

　

線形速度の無限大性　⇒　非線形速度の有限性（極限値としての光速ｃ）

　

に習って、

　

線形距離の無限大性　⇒　非線形距離の有限性（宇宙の地平面迄の距離）

　

論理の順番からすると、線形距離の無限大性を持った宇宙空間をギューッと押し

縮めて非線形に増減する距離の性質を備えた空間になる結果、無限大まで可能な

線形速度が押し縮められて光速ｃを極限とする非線形に増減する速度となったと

するシナリオの流れが自然かも知れない。

　この非線形の相対距離（！）を基にした定常宇宙論のモデルでは、宇宙は無限

の空間の様に観測されるが、有限の体積を持つ事となる。

しかし、この非線形距離の最大のメリットは他にある。

遠くの天体から地球に向けて伝播して来た光は、その道筋で距離の非線形の性質

に依り、徐々に膨張している空間を伝播する事により光の波長が伸びて観測され

る為に、宇宙の地平面により近い（つまり地球からより遠い）天体から放射され

た光ほど赤方偏移の割合が増加して観測される事となる結果、恰も、任意の宇宙

の地平面上の地点がビッグバンの爆心地となり、そこから宇宙空間が加速度的に

膨張している状態と同等の効果を観測する事となると推測する。

強力な指導原理となっている宇宙原理に些か抵触すると考える限局した或る地点

で宇宙が膨張を始めたと仮定するビッグバンの考えに比べ、非線形距離の概念は

むしろ宇宙原理の妥当性の根拠を与えるものと考える。

なお、宇宙原理並び相対性原理により、宇宙の任意の慣性系に於ける物理現象は

全て等しく生じるという前提が、非線形距離の概念でも成り立たなければならな

い事は言うまでもない。

二大の指導原理の一つである相対性原理の拠り所が、非線形速度の概念であり、

もう一つの指導原理である宇宙原理の拠り所が、非線形距離の概念という関係に

ある。

又、非線形距離の性質の宇宙を静的な宇宙空間の変化（静的膨張宇宙論）とすれ

ば、ビッグバン宇宙論は、動的な宇宙空間の変化（動的膨張宇宙論）という事に

なり、特異点の問題や宇宙の膨張を遂行する力の源となるダーク・エネルギー等

を仮定する必要性や、光速よりも速い速度で宇宙が膨張する事の合理的な説明の

必要性等を考慮すると、非線形距離の概念の導入だけで全てが論理的に説明可能

という新しい宇宙論の単純性が遙かに勝っている事は明らかであろう。

特に、宇宙空間の膨張という為には、空間とは何かという素朴な疑問の解明を始

め、ダーク・エネルギーなる未発見の物質の確認と、そのエネルギーがどの様な

機序で解析すら進んでいない空間という対象物を膨張させうるのか、しかもどの

様な機序で光速を越える速度で膨張させる事が出来るのかというこれ迄に物理学

の歴史上で最大の難問とも言える多くの課題を解決する必要がある。

膨張する空間の性質として、空間に存在する物質は光速を越える速度でお互いが

遠ざかっているが、この空間を伝播する光は膨張しない空間を伝播する光と同様

に光速不変の原理に従い常に光速ｃとして観測されるという説明は、一貫性を欠

いた理論と言わざるを得ない。

一例として、電子にニュートリノが衝突して、電子の速度が物質中の見かけの光

の速度を上回った場合には、電子が纏っている光の衣がはぎ取られて置き去りに

されて、チェレンコフ光という青白い光を発する現象があるが、宇宙の膨張速度

が光速を越えて更には加速度的に生じている状態で、果たして、この様な現象が

論理的に生じないことを保証する事が出来るかどうかも議論すべきと考える。

更に、加速又は減速状態で光速を越える速度で膨張している宇宙空間に於いて、

電磁気現象を始め全ての物理現象が矛盾無く成立している事を証明する事が必要

となる。

　

　これからは、非線形距離の概念を取り入れた宇宙モデルの理論に基づく厳密な

定式化を行い、これ迄の天体の観測結果と定量的に整合するか否かという検証の

作業が必要となる。

その為には、非線形の空間を対象とする新しい幾何学（非線形幾何学？）が必要

と考えるが、解析力学から発展したシンプレクティック幾何学は、非可換幾何学

とも深い繋がりを持っている事を考えると、シンプレクティック幾何学に非線形

の空間の概念を加えて拡張した新しい概念の幾何学の構築が必要となると考える。

なお、ＷＭＡＰ（ウィルキンソン・マイクロ波非等方性探査衛星）の観測結果に

依れば、スペクトルの低周波領域（宇宙を最大規模で観測したとき捕らえられる

姿）では、アルメニアの科学者のガーザディアンが調べた結果は、宇宙の最遠の

曲率がゼロ（宇宙は平ら）ではなくて負となり、ロバチェフスキーの双曲幾何学

のモデルに近いのではないかと考えられて来ている。

双曲幾何学のモデルを説明する際の好例として、エッシャーの「円の極限IV」が

引き合いに出されるが、この版画の円の中心から四方に離れるに連れて、図柄の

サイズが小さくなり、円周上になると図柄のサイズが無限小となる状態は、宇宙

の任意の観測地点から四方八方に遠ざかるに連れて、距離の非線形の性質により

空間が収縮した様に観測される事と類似している事となり、非線形距離の概念を

基本とする有限定常宇宙のモデルとの類似性も今後の検討課題と考える。

また、双曲幾何学を物理学に応用する好例として、 相対論に依れば、高速で回転

する円盤上では、ローレンツ収縮により物体の長さが縮む事となるが、このとき

円盤の中心から遠ざかるに連れて回転速度が速くなる為、ローレンツ収縮の効果

が強く出ることになるが、この様な場合では、二点間を結ぶ最短距離(円盤の直径

を除いて)は、回転の遅い中心寄りの線になり、止まった状態の円盤から見ると、

その線は曲線になる。

つまり高速で円盤を回転させた為に、直線が曲がり3次元の空間が負の曲率を持っ

た様になる為であり、この例も、非線形距離の概念を基にした場合の宇宙空間の

性質を比喩したものという事であるが、非線形の速度の概念の基では、相対論の

運動物体のローレンツ収縮など現実の空間で生じることが無い事は、言うまでも

無い。（巻末の参考文献（Ｖ））

ここで注意すべきは、非ユークリッド空間は絶対的！な空間の曲がりを想定して

いるが、非線形距離の概念では相対的！な空間（三次元の距離で構成）の短縮を

意味している事が最大の相違点であり、宇宙原理の要請からも必要な概念である

と考える。

以上の結果、ユークリッド空間を基本として、シンプレクティック幾何学の長所

併せ持った非線形距離の概念を基にした新しい幾何学の構築が有望なのかも知れ

ない。

　

ところで、非線形速度の概念と非線形距離の概念の妥当性を背景として、現行の

線形の数しか扱わない線形代数学に代わり、非線形代数学なる新しい数学分野の

必要性に関し、少し具体例を考える事とする。

　

非線形数のシンボルとして、数字の先頭にノを付加して、非線形数を明示的に表

す事とする。

このシンボルは、カタカナのノであり、線形である直線に対応する非線形である

曲線（非直線）をイメージしたものである。

　

そこで、或る規則で変化する非線形数（ノｘ）の加法則は、非線形数の接続係数

（仮称）をｋ（ノｘ）とすれば、

　

ノｘ2＝ノｘ0＋ｋ（ノｘ0）*ノｘ1

　

という形式で表現出来るものと想定する。

因みに、現行の数に関する概念は全て線形数であるが、数を非線形数の範疇まで

拡張した場合の、この数の接続係数が常に１という最も簡単な性質の数に該当す

る事となる。

　

ここで、具体例を示す。

非線形速度の加法則は、線形速度の変数をｖとして、これに対応する非線形速度

をノｖとし、光速をｃ（光速ｃは最大速度の不変量であり、非線形の数として敢

えて明示する必要は無い）とすると、

　

ノｖ2＝ノｖ0＋ｋ（ノｖ0）*ノｖ1

　

となるが、非線形速度の接続係数は、ｋ（ノｖ0）＝（ｃ−ノｖ0）／ｃと置ける

事がＤ節で証明出来ているので、

　

ノｖ2＝ノｖ0＋ｋ（ノｖ0）*ノｖ1

　　 ＝ノｖ0＋ノｖ1（ｃ−ノｖ0）／ｃ

　

となる。

尚、これまで、ガリレイ変換やローレンツ変換に於ける速度の加法則という名称

の方程式は、非線形速度の概念から観ると、速度という非線形数の加減算を表現

する為の線形数を使用した方程式という事になり、一般的な非線形の数の加減算

に拡張できる目処が付いたものと考える。

　

観測地点から宇宙の地平面までの距離（宇宙の半径）をｒｕとして、観測地点か

ら或る天体までの距離をｒとすれば、天体が存在する位置に於ける距離の収縮率

Ａ（ｒ）は宇宙の地平面に近づくほどゼロに漸近するという相対距離の非線形の

性質により、a,bは観測の結果集積されたデータを元に決定される定数とすると、

　

Ａ(r)＝(１−(ｒ／ｒｕ)^a)^b

　

という形式になると予想する。

尚、この予想の参考とした形式はローレンツ収縮率であり、ｒ及びｒｕがｖ及び

ｃに対応し、a＝2及びb＝1/2となるので、これを利用してＡ(ｒ)を仮に、

　

Ａ(r)＝√(１−(ｒ／ｒｕ)^2)

　

と置くことにする。

Ａ(ｒ)は、膨張宇宙論に於けるロバートソン・ウォーカー計量Ｒと類似の計量と

いう事になる。

尚、相対論のローレンツ収縮の概念や非線形速度の概念を用いた座標変換時に現

れる同等の空間の収縮効果は、元来、運動している物体の速度に起因する現象で

あるが、光のドップラー効果は、距離の非線形性にも同様な効果をもたらしてい

る事を考えると、光源の運動に起因するドップラー効果も空間の擬似的な収縮や

伸張として捉える事も有用かも知れないし、これが本質的な現象かも知れない。

つまり、これ迄は相対速度に応じてドップラー効果が生じているという解釈が行

われてきたが、相対速度を空間の疑似の変化（収縮や伸張）と見なせば、非線形

距離の性質である空間の相対的な収縮に依るドップラー効果（赤方偏移のみ）と

併せて、空間の変化という統一的な説明が可能となると考える。

　

非線形距離の宇宙モデルでの赤方偏移率Ｚ(ｒ)は、地球の観測者から観た距離

の収縮率Ａ(r)の空間にある天体の光源から放射された光が、地球の観測者という

距離の収縮率が１（全く収縮していない現行の線形距離の状態でＡ(０)＝１）の

空間（ｒ⇒０）に到達する間に、距離の伸張効果に依り光の波長が伸びる事によ

り生じると解釈すると、

　

Ｚ(ｒ)＝Ａ(0)／Ａ(r)−１

　　　＝√(１−(０／ｒｕ)^2)）／√(１−(ｒ／ｒｕ)^2)−１

　　　＝（１−√(１−(ｒ／ｒｕ)^2)）／√(１−(ｒ／ｒｕ)^2)　・・・（Ａ）

　

従って、赤方偏移率Ｚは、ｒがｒｕに漸近する事で、限りなく増大する事となる。

尚、式（Ａ）は、ローレンツ係数γと形式的に一致する事にも注目したい。

因みに、非線形の速度の概念では、ローレンツ係数は空間の伸張率と解釈される。

尚、ｒｕの値は、これまでの多くのＺ(ｒ）の観測結果から容易に推定される。

更に、全てのｒに対応するＺ(ｒ)の観測値を満足する様なa及びbを決定する事で、

真の値に近似するＡ(ｒ)の方程式が決定される事となり、最終目的である非線形

の相対距離の性質を表す方程式が定量的に決定されて定式化される事となる。

　

セファイド�Tａ型超新星の固有の明るさがどの場合も同じという理論的な裏付け

の基で、その超新星の明るさが距離の自乗に逆比例して減衰する事でそれが属す

る銀河迄の距離ｒが求められているが、その距離ｒはあくまで線形距離であり、

非線形距離は線形距離より短縮している事により近くに見える事となるが、天体

が位置している空間の見かけの収縮に依り天体の大きさが縮小している様に観測

されると思われるが、距離に関する全ての現象は相対的な見かけの現象である事

を考慮すれば、天体から放射された光は観測機器に到着する間に波長が伸び空間

的な広がりも拡大する結果、観測時（見かけ上）には、拡大した天体の像を観測

する事となり、この２つの要因を加味して、天体までの真の非線形距離ｒを導出

する事が必要となる。

つまり、遠い天体ほど大きく観測される為に、

　

（距離ｒの天体の真の大きさ）＝（天体の見かけの大きさ）×Ａ(ｒ)

　

という補正が必要となると考える。

巻末の参考文献（V)の（２）に於ける、アルメニアの天文学者のガーザディアン

の最深宇宙の宇宙背景放射の観測結果に基づく宇宙の曲率が負という判定結果は、

天体の見かけの大きさが拡大して観測されるという推定を実証する結果と考えら

れる。

　

これまでの天体観測の膨大なデータにより、赤方偏移率Ｚを縦軸に、天体までの

距離ｒを横軸にしてプロットしたグラフは、双曲線様の二次曲線を描いている様

に思われるが、この曲線が漸近する横軸の値が宇宙の地平面までの距離ｒｕとい

う事になる。

式（Ａ）のＺ（ｒ）とｒの関係は反比例の関係にあるが、このグラフを回転移動

すれば、双曲線のグラフとなる。

　

非線形の速度の形式から類推すると、非線形の距離ノｒ（ノは非線形の印）は、

　

ノｒ＝ｒｕ(1−Ａ(ｒ))

　　＝ｒｕ(１−√(１−(ｒ／ｒｕ)^2))　・・・（Ｂ）

　

この方程式は、縦軸をノｒ、横軸をｒとする中心が（０，ｒｕ）で半径ｒ0の円を

描く事となるが、これを叩き台として天体観測に厳密に一致する方程式に修正す

る事が今後の課題である。

　

ここで、非線形距離の加法則を考える。

非線形速度の加法則の形式に準じて、観測地点から宇宙の地平面迄の非線形距離

ｒｕ（非線形距離の最大値）が光速ｃ（非線形速度の最大値）に対応すると仮定

して、暫定的に、

　

ノｒ2＝ノｒ＋ノｒ1*(ｒｕ−ノｒ）／ｒｕ

　

と仮定するが、非線形の距離ノｒ1は負の値も取り得る（正確には、減算も可能）

と推定している。

尚、観測地点から或る天体までの非線形距離をノｒ、更にその天体から順方向

（又は逆方向）にノｒ1（その天体から観測した非線形距離）だけ離れた天体があ

るとした場合の、観測地点からその天体までの非線形の距離をノｒ2とする。

尚、ｒｕは任意の観測地点から宇宙の地平面迄の非線形距離（最大値）であるが、

光速ｃと同様に不変定数であるので、線形や非線形に拘わらず同じ値となる定数

である。

これで、論理的に導き出されている物理学的に意味を持つ最小の距離の単位であ

るプランク長から最大の距離としての宇宙の地平面までの距離が決定される事と

なる。

　

速度は任意の観測者が観測した観測値という相対的な物理量（相対速度）である

事から、距離も任意の観測者が観測した観測値という事で、相対距離という新し

い概念が必要となるものと考える。

ただし、相対距離の概念が必要なスケールの距離は宇宙規模で有り、太陽系が属

する銀河系程度のスケールでは、距離を近似的に絶対距離と見なしても良いので

はないかと考える。

ただし、相対論の相対距離（ローレンツ収縮効果による）を否定した非線形速度

の概念上の距離とは、この近似的な絶対距離が該当する事になる。

また、或る２つの物体の速度の差という概念で速度差という物理用語に対応して、

距離に関しても、或る２つの物体間の距離の差という概念で、距離差（長さ）と

いう物理用語を定義する事も必要と考える。

最大の速度差としては、反対方向に伝播中の２つの光の速度差２ｃという事にな

るが、一方、最大の距離差としては、観測地点からの或る方向の宇宙の地平面と

観測地点から正反対方向の宇宙の地平面の間の距離（即ち宇宙の直径）２ｒ0とい

う事になる。

なお、速度差や距離差は線形の物理量という事になるであろう。

　

大海の船乗りが、地平線(地の果て)を目指してひたすら真っ直ぐ航海して地平線

の近く迄到達すると、何と同じ距離に地平線を認める事となり、更にそこを目指

して更にひたすら真っ直ぐ航海し続けると、更にその向こうに地平線を認めると

言う様に、これを繰り返す内に何と出発点に戻ってくるという船乗りにとっては

何とも不思議な体験をする事になるが、宇宙船の乗組員も同様な体験を行う事に

なると思われる。

これは、宇宙に充満している自由素光子が光速で運動しながら均一な密度を保つ

為には絶対必要な宇宙の構造と考える。

　

ニュートン力学の時代の線形で無限大まで許容される速度の概念と非線形速度の

相対的な有限性の対比を考えると、線形で無限遠まで許容される現行距離の概念

に対し、非線形距離の概念では、距離の有限性が自ずから課される事となり、

この性質こそが、果てはないが有限な宇宙の構造を可能としている根本原因とも

考えられるが、我々が三次元空間に存在している訳ではあるが、直接に認識する

ことが不可能な余剰次元を付加した四次元の世界が我々が存在している宇宙の真

の空間構造と考えると、この余剰次元の効果の一つが距離を非線形の性質に規定

している根本原因とも考えられる。

尚、余談であるが、ミクロの素粒子の半整数のスピンの性質と宇宙規模のマクロ

の非線形距離の性質に基づく空間の有限性とは、スケールの両極に位置している

大変不思議な性質である。

四次元空間の存在を仮定する事により、三次元空間に住んでいる我々にとっては

実感する事が不可能ではあるが、数学の強大なパワーを借りれば何れも容易に成

り立つ事を証明出来るかも知れない。

　

ハーバード大学のリサ・ランドール教授が、１９９８年に、この世の時空間から

消滅しては又現れる素粒子の不思議な動きを解明しようと考えて、宇宙を五次元

（四次元の空間＋時間軸）とする理論を発表している事にも注目したい。

常套の手段として、次元を一つ下げて三次元空間の平面を我々が住んでいる宇宙

と仮定すると、空間を通り二次元の平面上に到達した物質は、恰も次元を超越し

てＳＦで俗に言うワープして来た様に観測されるものと思われる。

但し、空間を通る事による時間を消費する必要性から、時間を超越（瞬間移動）

する事は不可能と考える。

果たして、ランドール教授が発見したという素粒子の消滅と出現が空間を超越し

た現象であったのであろうか？

２００７年からCERNのLHCでこの実証実験が始められているとの事で、その成果を

期待したい。

　

宇宙の地平面の近傍の天体の物理現象はどの様な状態にあるのかという事が今後

の研究課題である。

非線形距離の性質としての空間の収縮が存在するとした場合は、空間の収縮に応

じて光の速度も低下する事が推測される。

　

観測される光速ｃ(ｒ)＝ｃ*Ａ(ｒ)≦ｃ

　

なお、短縮した空間を速度が鈍化した光が伝播する事となり、時間は不変に保た

れる事となる事がと推測される。

観測地点から距離ｒの空間に位置する天体から放射された速度ｃ(ｒ)の光が空間

を伝播する間に空間の静的な膨脹に従い速度が増加し、観測地点では光速ｃとし

て観測機器にこの光が捕捉される際に、空間が膨脹した効果としての赤方偏移を

観測する事となるが、この赤方偏移を動的な空間の膨脹の効果と解釈しているの

が、ビッグバン宇宙論という事になる。

尚、ビッグバン宇宙論では、ビッグバンが生じた位置（絶対的な位置）から或る

宇宙の空間の位置迄の距離に依り、その空間の拡張率（膨張率）が絶対的に決定

される事となるが、その結果、相対性原理に反する現象が生じる事が予想される

事になるかも知れない。

果たして、観測地点から距離ｒの空間に存在する天体から放射された光の速度が

ｃ(ｒ)として観測されるかどうかという事であるが、その近傍の天体間の光に依

る相互作用の観測から可能と考えるが、相対性原理の要請から、重力の伝播速度

が光の伝播速度と等しいという仮定の基で、超新星爆発の際の発光の振る舞いや

クウェーサの運動や連星間の重力相互作用を観測する事で容易に実証実験が可能

となると考える。

そこで、時空の歪みを重力場と解釈している一般相対性理論の是非が試される事

にもなろう。

　

ここで、質量を有する物質の運動状態を考えると、観測地点から物体までの相対

距離をｒとすると、観測者の近傍での物体の速度はｖ(０)（ｒ⇒０）であるが、

空間の収縮に依り物体の速度ｖ(ｒ)はｖ(０)より低下（物体の運動の鈍化）する

事となると予想されるので、

　

線形の速度；ｖ(ｒ,ｖ)＝ｖ(０)*Ａ(ｒ)

　

ここで、ｖ(０)を非線形速度で表せば、

　

非線形速度；ﾉｖ(ｒ,ｖ)＝ｃ(１−√(１−(ｖ／ｃ)^2))*√(１−(ｒ／ｒ0)^2)

　

更に観測上の光速ｃ(ｒ)＝ｃ*Ａ(ｒ)を考慮すると、観測地点からｒの距離の空間

に於ける物質の最高速度は、ｃ(0)（＝ｃ）からｃ(ｒ)に低下する事となるので、

√(１−(ｖ／ｃ)^2)内のｃをｃ(ｒ)に置き換えて、

　

非線形速度；ﾉｖ(ｒ,ｖ)＝ｃ(ｒ)(１−√(１−(ｖ／ｃ(ｒ))^2))・・・（Ｃ）

　

となる事が推測される。

式（Ｃ）は、光を含めた全ての物質が、収縮した空間に於いて一様にその運動が

鈍化している事を表している。

これは、遠くの現象を観測する場合に、視覚効果にて、全ての物質が恰も縮小し、

全ての物質の運動が恰も鈍化した様に錯覚される事と似た様な現象である。

この結果は、特殊相対性理論に於ける時間の遅れに起因する物質の運動の鈍化が、

光速不変の原理を前提としている為に、光の速度には影響しない事と対照的であ

るが、ローレンツ収縮は物質の運動の鈍化を空間の架空の収縮で肩代わりした物

と考えると、当然の結果と思われる。

以上の結果、非線形の速度を宇宙規模に拡張すれば、非線形距離の性質を考慮す

る事が必要となり、観測者の近傍の空間の光速ｃ(ｃ(0))を、観測上の見かけの

光速ｃ(ｒ)に置き換えた場合の非線形の速度という事になる。

つまり、現行の慣性系の座標変換は、相対速度のみに依存する変換で事足りてい

たが、宇宙規模の現象を対象とする宇宙論の分野では、更に相対距離に依存する

見かけの光速の変化を考慮した慣性系の座標変換が必要となるという事である。

　

次の段階として、任意の収縮した空間に於いて、相対性原理を満足する物理現象

が生じている事を証明する事が必要である。

観測地点の近傍（ｒ≒０）の収縮率１の空間に呼応して、光速がｃ(ｃ(0))という

不変値で観測されている空間状態に於いて、非線形速度を導入した新しい力学が

相対性原理を強く後押ししている事を考えると、任意の相対距離に位置する空間

まで拡張した自然現象も、距離と速度のスケールの違いのみであり、相対性原理

が等しく成立するものと予想する事ができる。

これまで、空間は空虚な空隙であると推測してきたが、非線形距離の性質に依る

空間の収縮に伴い、光も含めて全ての物質の速度が一様に低下する結果の予測を

得た事は、空間と物質（の運動）との間には密接な関係が有る（独立では無い）

事が浮き彫りになってきたという事で、重要な結果と考える。

なお、素光子一元説（全ての物質は唯一の基本粒子である素光子の集合体）に従

えば、任意の距離の空間に於ける自然現象において、素光子の総数は時間発展並

びに座標変換に於いて不変（⇒エネルギー不変の法則の根拠）であり、物理法則

の基本的な原理に位置している事となる。

ここで、一つの問題として、空間が収縮した状態にある遠くの天体のエネルギー

密度が空間の収縮率Ａ(ｒ)の３乗に逆比例して増大することとなり、このことが

相対性原理に抵触する可能性はどうかという事である。

素光子の固有エネルギーは素光子の運動エネルギーであるので、収縮率Ａ(ｒ)の

空間に於ける素光子の速度がｃ*Ａ(ｒ)に減速していることを考えると、素光子や

素量子の固有エネルギーはＡ(ｒ)の二乗の割合で減少していると考えられる。

そうすると、プランク定数もこの割合で減少しなければならない。

更には、空間の収縮に伴い、素粒子のサイズも縮小されなければならなくなり、

最小の長さとしてのプランク長もその例外とはならないであろう。

更には、万有引力の加速度が距離の自乗に逆比例する事から、距離の短縮率Ａ

(ｒ)の二乗の逆数の割合で増加する事となるので、力の不変性から重力定数Ｇが

その割合で減少する必要が生じるかも知れない。

なお、論理的にも絶対的に不変な物理量は、素光子（素量子）の個数であろう。

更に、素光子説に基づく質量（慣性質量及び重力質量）の本質的な概念は、物質

を構成している素光子や素量子の個数という事から考えると、質量は不変のまま

で済むのかも知れない。

果たして、不変定数と考えられている光速ｃやプランク定数ｈ及び万有引力定数

Ｇが減少した状態の空間で相対性原理が満足されるかどうかを論証する事が今後

の課題である。

巨視的に考えると、我々が住んでいる地球の近傍の空間の収縮率が１の環境下に

て成立している物理法則を、距離ｒ離れた収縮率Ａ(ｒ)の空間に適用する際には、

基本的な物理量である距離、速度、光速、プランク定数、更には、万有引力定数

が空間の収縮率Ａ(ｒ)に従い一様に減少したミニチュア的な環境の基で成立して

いるという視点から観れば、相対性原理が宇宙の任意の空間で成立している事は

意外と容易く説明できるかも知れない。

尚、目下の結論からは、宇宙が四次元超球の表面という果ては無いが有限の閉鎖

空間であると仮定すれば、宇宙に充満している素光子の総数は常に一定で有り、

任意の空間の素光子の密度も定常の状態にある事が推測されることとなり、この

条件下では地球上である現行の物理常数が等しく適応される事が推測される。

　

　これまでの考察に依り、本来の全ての自然現象は、非線形の物理量が織り成す

非線形現象である可能性が強いと考えられる。

つまり、これまでに線形の性質の表れと解釈して観測されてきた全ての現象は、

非線形現象の近似的な一断面を観測しているに過ぎないのかも知れない。

　非線形速度の導入により、相対性原理の正当性を強く支持する事が出来ると考

えるが、宇宙原理の妥当性の為には、この非線形距離の概念が必要であろう。

ところで、非線形の速度及び距離の性質を表す方程式の形式の類似点を考えると、

非線形の速度と距離は、独立した自然の基本的な性質では無く、もっと基本的な

原理（四次元宇宙の摂理）から派生している副次的な自然の性質と考えるべきで

あろうか！？

非線形の速度及び距離の概念を導入した四次元の幾何学の解析結果に期待する。

ところで、人為的に定義した観念的な物理量である時間だけは、絶対的な線形の

物理量のままにしておく事がシンプル性を重んじる物理学では相応しいと考える

訳であるが、これからの物理学の新しい指導原理とすべきとも考える。

　

ここで、幾何学に関する大変興味深い成果を述べる事とする。

数学者のワイルの純数学のゲージ理論を物理学で応用したヤン・ミルズ理論を、

数学者のドナルドソンが純数学の四次元ユークリッド空間の多様体に里帰りさせ

て取り入れた結果、１９８２年に微分構造が無限に存在するというドナルドソン

の定理を発見したという事である。

この事柄を非線形距離の概念から眺めると、距離が線形の物理量である事は自明

の理と考えられている現行の数学理論に於いて距離の微分構造を求めると、本来

は距離が非線形に変化する数である為に、距離の微分の結果は不定となり、この

結果を線形の概念しか想定していない現行の数学理論では微分構造が無限に存在

するという解釈しか出来なかったと解釈する事が出来る。

この様に考えると、ドナルドソンの定理は、四次元ユークリッド空間が非線形に

変化する距離の性質を帯びている事を純数学的に証明したものと考える。

今後、幾何学の専門家による厳密な検証が必要である。

ハッブルの法則が、非線形距離の概念を天体の観測結果で証明している事実と考

えると、ドナルドソンの定理は、純数学の立場での論理的な非線形距離の概念の

必要性を要請するものであると考えると、非線形距離の概念は、論理的及び天体

観測の両面で支持される強固な概念であると考える。

　

E節＞非線形物理量の基本的性質

　現行の数学を始めとする全ての学問で取り扱う数は、１＋１＝２、２＋１＝３

と言う様に専ら線形に変化する数に限られている。

これは、古代の人々が生存の必要性に迫られて、物の個数（整数）を数える事の

必要性から数の概念が生まれた時代からの自明の事柄と考えられて、これ以上に

数の概念を拡張する必要性が今日まで生じなかった為と考える。

文字通り数を論理的に取り扱う学問が数学であり、線形代数学に象徴される様に、

線形に変化し無限大まで許容される数しか研究の対象とはなっていない。

　

物体の運動の観測事実から、観測する立場の違いで同一の物体の運動速度が異な

って観測される相対的な物理量という事が自明の理として何の疑いも無く極当た

り前の現象として受け入れられているが、深く考えると大変不思議な現象である。

自然は、相対的な物理量を備える事により、任意の慣性系の物理現象が同等に生

じる事を巧妙な仕掛けで可能にしている物と考えると、相対的な物理量は非線形

に変化する物理量でなければならないという事に気付く事となる。

なお、無限大や無限小という概念は、数学上の具体的な数には属さない数の大き

さを表現する象徴的な意味合いの記号であり、自然の仕組みを研究の対象として

いる物理学には馴染めない概念である。

従って、無限大や無限小という概念を許容する物理量を用いた論理は、矛盾した

結果を生じる事を覚悟すべきである。

従って、基本的な物理量は、無限大まで許容されるべきでは無く、最大値を持つ

事が論理的に必要であると考える

　

以上の事柄を要約すると、非線形の物理量は、非線形に変化し最大値（極大値）

を持ち、相対的な物理量という事になる。

光の速度が任意の慣性系で一定値ｃとして観測される事に関して、一見すると、

光の速度は相対的では無く絶対的な速度の様に錯覚されるが、距離の最大値とし

ての宇宙の地平面が任意の観測地から等距離に認められるという相対的な物理量

の最大値と同様に考えると、全ての物質中で最高の速度で運動している光の速度

が任意の慣性系で一定値ｃとして観測されなければならない事は当然という事に

なる。

　

ところで、非線形速度の概念と非線形距離の概念の妥当性を背景として、現行の

線形に変化する数しか取り扱わない線形代数学に代わり非線形代数学なる新しい

数学分野の必要性に関して、少し具体例を考える事とする。

非線形数のシンボルとして、数字の先頭にノを付加して、非線形の数を明示的に

表す事とする。

このシンボル・マークはカタカナのノであり、線形である直線に対応する非線形

である曲線（非直線）をイメージしたものである。

　

　非線形数は無限に想定する事が可能であるが、目下は線形方程式で表現可能な

非線形数のみを対象とする事にするが、少なくとも非線形の物理量は全て何らか

の線形方程式で表現する事が可能であると推測している。

そこで、或る規則の元で変化する非線形の数（変数ｘ）の加法則は、非線形の数

の接続係数（仮称）をｋ（ｘ）とすれば、

　

ノｘ2＝ノｘ0＋ｋ（ノｘ0）ノｘ1

　

という形式で表現出来るものと想定する。

この方程式は、非線形の数；ノｘ0に非線形の数；ノｘ1を加減算する場合の解で

ある非線形の数；ノｘ2を表す方程式である。

因みに、現行の数学理論で専ら取り扱っている線形の数は、接続係数ｋが常に１

という非線形の数の範疇の最も単純な性質の数という事になる。

　

ここで、具体例を示す。

速度は一般的に慣用的にｖという変数を用いているので、非線形速度の加法則は、

最大値である光速をｃとして、

　

ノｖ2＝ノｖ0＋ｋ（ノｘ0）ノｖ1

　　 ＝ノｖ0＋ノｖ1（ｃ−ノｖ0）／ｃ

　

となる。

ここで、非線形距離の性質を表現する方程式を推定する事とする。

非線形速度の最大値である光速ｃに対応する非線形距離の最大値は、任意の観測

地点から宇宙の任意の方角を観測した場合の宇宙の地平面までの距離である宇宙

の半径Ｒｕという事になるので、非線形距離の加法則は、非線形速度の加法則の

式の接続係数ｋに習って、

　

ノＲ2＝ノＲ0＋ｋ（ノＲ0）ノＲ1

　　 ＝ノＲ0＋ノＲ1（Ｒｕ−ノＲ0）／Ｒｕ　・・・（Ａ）

　

の方程式で表現出来るものと推定する。

この式は、非線形速度の場合と同様に、非線形の距離の加算が、距離の最大値で

ある宇宙の半径Ｒｕ（宇宙の地平面）に近づくに連れて頭打ち状態になる事を表

している。

　

式（Ａ）に於いて、距離ノＲの地点の空間から観測地点の空間までの静的な空間

の膨張率Ｚ（ノＲ）は、

　

Ｚ（ノＲ）＝ｋ（0）／ｋ（ノＲ）−１

　　　　　＝（（Ｒｕ−0）／Ｒｕ）／（（Ｒｕ−ノＲ）／Ｒｕ）−１

　　　　　＝Ｒｕ／（Ｒｕ−ノＲ）−１

　　　　　＝（Ｒｕ−（Ｒｕ−ノＲ））／（Ｒｕ−ノＲ）

　　　　　＝ノＲ／（Ｒｕ−ノＲ）

　

となり、この静的膨張率Ｚ（ノＲ）は実際に観測されている赤方偏移率と論理的

に一致しなければならないが、非線形距離の性質を表現する方程式を決定する事

が先決である。

ただし、距離の非線形の性質を求める拠り所は、目下の所は天体迄の距離に比例

する赤方偏移率の変化という観測事実だけである事を考えると、この観測結果を

用いて距離の非線形の性質を表す方程式を推定する手段しか出来ない。

次の段階として、この距離の非線形の性質を表す推定式が他の全ての観測事実と

整合しているかどうかの検証が必要になる。

速度が観測者の違いにて観測結果が異なる相対的な物理量である事は、自明の理

として、何の疑いもなく受け入れられて、深く考察された事が無い様に思われる。

別の見地から観れば、速度が非線形の物理量である為に、速度が相対的な物理量

として観測されるという事になる。

そこで、距離を非線形の物理量に変更すれば、距離も相対的な物理量という事に

なり、指導原理としての宇宙原理（宇宙は大域的に見れば、一様、等方である）

を容易に支持する根拠を与える事が出来る。

これと表裏一体のもう一つの指導原理である相対性原理が、非線形速度の概念に

より強力にサポートされる事も納得される。

　

アインシュタインは、時空に物理現象を生じさせる原因となる性質を課す必要性

を説いていたが、素光子説では空間（時間は空間とは独立している）は文字通り

の空虚な間隙であり、その空隙を光速ｃで飛び交っている自由素光子場こそが、

森羅万象を生じる原因であると考えるので、物理的な性質を備える必要も無い。

また、遠くの天体の光ほど赤方偏移が強く観測されるという事実を説明する理論

として、現行の宇宙論の中で、ビッグバン宇宙論では宇宙が加速膨張を行ってい

ると解釈されているが、時空に物理的な構造を仮定すると、その構造自体が膨張

しているという事になり、多くの解決すべき難題が生じる事を覚悟すべきである。

　

尚、数学の点（位置情報のみを有し、領域を持たない空間の概念）を基本単位と

する集合体としての空間の概念の困難を回避する手段として、先ず三次元の空間

を定義し、その分割により二次元平面や一次元の線を定義し、更に線の分割を行

うという考えが提示されているが、従来の考えとは全く逆説的ではあるが、理に

叶った考えと思われる。

　

物理現象を記述する上で最も重要な物理量である速度及び距離を線形から非線形

に変更する事は、物理学全般に渡る基本概念の変更をもたらすばかりでは無く、

物理学の強力な道具としての数学の基本概念（非線形の数の概念や速度に関する

微積分の概念）も根本的な再構築を余儀なくされる事は必定と思われる。

現行の線形の数を前提とする線形代数学を拡張し、非線形の数を扱う事が可能と

なる非線形代数学の建設を望むものである。

これにより、多くの非線形現象（カオス、フラクタル、ソリトン、非線形光学）

の研究も飛躍的に発展し、非線形の物理量の概念を用いる事により、比較的単純

な方程式の形式で厳密解を導出する事が可能となるものと考える。

　

素量子の運動状態式の一つの解として、素量子の集合体としての、質量を有する

物体の速度が光速ｃに近づくに連れて速度の加算が頭打ちになる現象を発見し、

この現象を現行の理論（特に特殊相対性理論）に適用しようと考えた末に思い付

いたのが、非線形速度の概念である。

現行の速度を線形から非線形に変更すると、任意の慣性系に於ける任意の方向の

光の所要時間を静止時と等しくする様に、非線形速度の性質を決める事が可能で

ある事を確認している。

この意味する事は、慣性系の座標変換に於いて時間と空間を不変に保つ事が可能

となるという事である。

これで、一世紀待ちに待った絶対不可能と考えられてきた自然の絶妙なパズルの

一つがやっと解けた事になる。

　

現行の理論では、速度は単一の因子であり、線形に変化する物理量という前提で

全ての物理理論が構築されている。

しかし、素量子の運動状態式を基にした素量子の集合体（質量を有する物体）の

振る舞いから非線形速度の概念が導かれた事を考えると、速度とは、単一の因子

を表現している物理量では無く、因子が複合した状態を観測している事になる。

これは、温度とは、複数の粒子の運動状態の程度の平均を評価する物理量であり、

単一の因子を評価する物理量では無い事に例えられる。

現行の理論では素粒子と考えられている電子やニュートリノも、陽子や中性子の

様な複合粒子と同様な速度に関する振る舞いを行っている事を考えると、電子や

ニュートリノも、複合粒子である事が示唆される事となる。

すると、真の素粒子であれば、複合粒子の運動状態とは異なる速度の性質で運動

する事になる可能性があり、そこで素光子説の立場で眺めてみると、真の素粒子

は素光子（及び素光子の束縛状態である素量子）という事になるが、素光子は常

に光速ｃでしか運動出来ず、或る意味では、この推測が当たっているという事に

なる。

なお、素量子は、束縛状態の素光子という事で、単独の素粒子（素光子）として

の振る舞いが抑制されている状態の為に、複合粒子と同じ振る舞い（本質的には、

素量子の振る舞いが複合粒子の振る舞いを決定している）を行っているという事

になる。

　

ここで、本題に移るが、現行の理論で前提としている速度が単一の因子を表現し

た物理量と見なせば、数自体を現行の線形に変化するという自明と解釈されてい

る概念から非線形に変化する事も許容する様に拡張する必要性が生じる。

目下の速度に関して考察している事柄は、これに沿った事柄であり、数を非線形

まで拡張し、現行の線形数は非線形数の範疇の最も単純に変化する数という位置

付けになる。

これは、素光子説を意識せず、現行の全ての理論で受け入れる事が可能な速度の

概念という事になる。

一方、速度を複合の因子の表現という本来の立場を貫けば、数は線形に変化する

という概念で十分であり、物理学的には非線形に変化する数まで拡張する必要は

無いという事にもなる。

但し、非線形数の概念は、純数学的には興味津々の未開拓の新分野という事も言

える。

　

ところで、もう一つの非線形の物理量としての非線形距離の概念の必要性を考え

ているが、現行の理論では、距離とは単一の因子から成り立っている事が自明の

理と考えられている。

すると、矢張り、距離という物理量でも非線形数の概念が必要という事になるが、

四次元ユークリッド空間に於けるドナルドソンの定理が非線形距離という物理量

の性質を数学的に表現するものであると見なせば、非線形距離の性質は、宇宙の

構造が反映したものであり、或る意味、複合の因子の表れと解釈する事が妥当と

なり、この理由により、非線形数の概念は必要では無いという事にもなる。

　

何れにしても、速度及び距離を線形から非線形の物理量に変更する必要性から、

複合因子としての性質を表す関数又は非線形数の形式でこれらの物理量を表現す

る事が必要であるが、どちらの場合でも、結果的には複合因子としての性質を表

す関数として表現する事で目的を達成する事が出来るものと考える。

非線形数を扱える非線形代数学が確立されると、この様な関数を介する必要もな

く、直接非線形の物理量を演算する事が出来る様になるものと考える。

尚、非線形の物理量の微分積分は従来の方法では不可であり、差し当たり非線形

の物理量を表す関数全体を従来の方法で微分積分を行う事で達成できると考える。

　

E節＞宇宙の構造

　ニュートンの万有引力の作用機序を説明する試みの一つである１８世紀の中頃

に発表されたLeSage（ル・サージュ）の重力理論は、現在では見捨てられた過去

の遺物と化しているが、大変注目に値する理論と考えている。

この理論は、宇宙に均等に分布しているガス状の微粒子の運動を物体が遮蔽する

事で、２つの物体間の微粒子の密度が低下し、２つの物体に働く微粒子の衝突に

よる合力がお互いを接近させる方向に働く事で、万有引力として観測されるとい

う考えである。

この微粒子の候補としては、カシミール効果等で実在が証明されている量子力学

の零点エネルギー（素光子説に於ける自由素光子場に相当）が考えられる。

重力の発生機序がLeSageの重力理論で説明できる事となれば、宇宙空間の構造は

歪みのない平坦なユークリッド空間という事になり、現在の最新のマイクロ波の

宇宙背景放射の観測機器であるＷＭＡＰの観測結果とも合致する。

但し、宇宙の最遠の宇宙背景放射のマップでは、宇宙空間が負の曲率状態（双曲

幾何学の様な空間が収縮状態として観測される）ではないかという研究結果もあ

り、これこそ、距離の非線形性の新たな観測データではないかと考える。

すると、宇宙空間は三次元ユークリッド空間で、宇宙の地平面までの距離を最大

値とする非線形の性質を持った距離の概念で構成されているのではないかという

推測が出来る。

更に推論を進めると、宇宙は有限ではあるが果ての無い空間で成り立っている事

が現在の科学者の共通した希望的予想とすれば、距離の非線形で相対的な性質に

より、任意の方角の等距離に宇宙の地平面を観測し、その近傍まで行けば、更に

そこから任意の方角の等距離に新たな宇宙の地平面が観測される事が予想される

事となるが、地上の航海者の様に宇宙を一周して元居た場所に戻ってくるという

条件をクリアーする事は、三次元ユークリッド空間のままでは困難と考える。

そこで、我々が感知不可能な余剰次元の存在を仮定して、宇宙空間をもう一次元

増加して四次元ユークリッド空間と仮定してみると、三次元ユークリッド空間の

距離が非線形の性質を帯びている原因は、余剰次元の効果ではないかという推測

が出来る。

更に都合が良いことに、四次元宇宙（四次元超球）の性質の研究の成果として、

地上の擬似の二次元平面上の大海の航海者が地平線を目指して一直線に航海する

と出発した元の位置に戻ってくるという当事者にとっては非常に不思議な現象に

類似して、宇宙旅行のパイオニアは、一直線に宇宙を果てしなく航行していると、

いずれは出発点に戻って来る事になり、四次元ユークリッド空間の四次元超球の

表面（三次元空間）こそが求めていた有限であるが果ての無い宇宙の構造に適す

るモデルという事になる。

　

そこで、四次元ユークリッド空間の構造と性質を研究する幾何学のこれ迄の成果

を調べてみると、１９８２年にドナルドソンが発見した四次元ユークリッド空間

は、他の次元では認めない可微分構造が無限に存在可能（ドナルドソンの定理）

という驚くべき性質の帰結があり、この純数学上の性質は、物理学的には距離が

非線形の性質であるという事と等価ではないかと推測している。

（専門家による厳密な検討が必要である。）

その理由は、非線形の物理量の性質として、滑らかな変化を行う性質があれば、

勿論、微分可能という事になるが、微分の結果の値が一意的には決まらず、不定

（無限に存在する）という性質を持っている事に依る。

数学は、自然科学の探求には絶対不可欠な物理学と共に両輪の片方を担ってきて

いるが、四次元ユークリッド空間の距離の非線形性が純論理的で極自然に導出さ

れた経緯を振り返ると、これは正に曖昧さを完全に排除した純論理的に展開する

数学の独壇場であり、数学の絶大な威力をまざまざと見せつけた最も顕著な例で

あると考える。

これは、数学が自然の真理の的を正確に射貫いた結果と解釈出来ると考える。

一見すると、森羅万象という非常に多彩に観える自然の摂理は、単純で論理的

（合理的）に成り立っているに違いないという自然観を、この数学の成果で更に

確信出来る事になる。

　

この四次元ユークリッド幾何学に於ける距離の非線形の存在を純数学的に予言す

る解がどの程度まで非線形距離の性質を定量的に表現出来るかは不明であるが、

少なくとも、天体迄の距離に比例した赤方偏移の観測結果と合わせれば、距離の

非線形の性質を表す方程式がほぼ正確に求められる事になるものと考える。

　以上の考察の結果、宇宙の構造は四次元ユークリッド空間であると結論付ける

事が出来るものと考える。

ところで、宇宙の大きさを推測する術を考えると、自然現象の主役であるが唯一

の物質と考える素光子の速度（光速ｃ）が、宇宙の比較的大きな構造を規定して

いる可能性があると考える。

その根拠は、これまでに観測されている天体現象が安定した定常状態に保たれて

いる為には、宇宙規模の天体間の相互作用を演じている重力や電磁気力が伝達す

る速度が大きく関与している可能性があると考えるからである。

つまり、宇宙の大規模構造と光の速度が適当に調和する事が、宇宙の森羅万象を

安定した定常状態に保つ為の必須条件ではないかと考える。

そこで、銀河を宇宙の基本単位と見なして、先ずは、銀河が安定して定常状態を

保つ事が出来る条件を考えた場合に、銀河の構成要素である恒星同士の相互作用

を司る重力相互作用が遅滞なく遂行される為の重力の伝達速度である光の速度の

下限を規定する必要条件を見いだす事が必要と考える。

　

宇宙が四次元ユークリッド空間であるとすると、我々が何故三次元ユークリッド

空間しか感知できないのかという素朴な疑問が湧くが、これまでに二つの有力な

説が発表されている。

一つは、１９２０年代にクラインが考えた、遠くのホースは線として観測される

が本当は平面がロール巻き状の三次元構造であり、ロール巻きのスケールが電子

等の素粒子以下のスケールであれば、我々はこの構造を確認する術を持つ事が出

来ず、この様な状態での余剰次元が隠される形式を次元のコンパクト化と呼ばれ

ている。

もう一つは、我々は四次元空間に構造的に閉じ込められていると考えるブレーン

宇宙の考えであり、三次元空間というブレーンが四次元宇宙に埋め込まれている

という考えである。

この考えの希望的な予想として、ワープというＳＦの次元の跳躍を利用して、遠

くの天体まで瞬時に移動する方法が夢想できる事である。

更に新しい考えとしては、四次元ユークリッド空間の四次元超球の球面が、我々

が知覚できる三次元宇宙という事になり、四次元超球の表面の性質こそが距離の

非線形として、我々が感知可能となっていると解釈する事が出来る。

果たして、四次元超球の更なる性質を我々が観測できるかが今後の課題であろう。

　

ポアンカレ予想の成果を踏まえて、宇宙の構造を考えてみる。

我々が住んでいる宇宙がどの様な構造になっているのか解明したいという、古代

からの究極的な願望がある。

昨今の幾何学の驚異的な発達により、我々三次元空間の住人が直接感知出来ない

高次元の空間を定量的に推測する事が可能となって来ている。

「単連結な3次元閉多様体は3次元球面S3に同相である。」という、砕いて言えば、

三次元の有限の宇宙の構造は論理的に球体でなければならないという、１９０４

年のポアンカレの予想が、１世紀振りにロシアのペレルマンにより証明された事

は記憶に新しい数学の画期的な成果であるが、宇宙論（天文学）で、この成果を

利用しようという動きが極めて鈍い様に感じる。

宇宙に境界があるとすると、その境界はどの様な構造であるか、その外側はどの

様な構造になっているかという次々に湧く疑問で忽ち行き詰まる事になる。

そこで、宇宙は果て（境い目）の無い無限の広がりを持っていると仮定すると、

有名なオルバースのパラドックが生じるし、第一に、無限という数学上の架空の

概念は、自然を研究の対象とする物理学には馴染めない概念と考える。

そこで、有限ではあるが果て（境界）の無い宇宙を考えた場合に、三次元空間で

はこれを満足する事は出来ず、余剰次元を考えざるを得なくなる。

そこで、先ず、三次元に一つの余剰次元を加えた四次元空間を考えてみる。

因みに、四次元球面のポアンカレ予想は、既に１９８２年にフリードマンが証明

し、フィールズ賞が授与されている。

つまり、宇宙が五次元空間の場合は、五次元超球（四次元球面）が宇宙の構造と

して適する事が証明された事になる。

　

ここで、地球という有限の球体の表面を擬似平面と見なしてみると、地上の旅人

にとって、任意の位置から観て四方の等距離に地平線という擬似の地上の果てを

認める事となり、任意の方向の地平線を目指して一直線に進み地平線まで辿り着

くと、そこは地上の行き止まりでは無く、四方の等距離に新たな地平線を認める

事となり、更に限りなく地平線を目指して一直線に進むと、いずれは元居た場所

に戻ってくるという不思議な体験をする事となる。

この様な体験が出来る環境こそ、有限で果ての無い宇宙の構造に相応しいと考え

る事が出来る。

そこで、四次元空間の場合は、四次元超球が正に該当する事になる。

四次元超球の表面が目的の宇宙の構造と仮定すると、地上の旅人の体験に習って、

宇宙の任意の地点の宇宙飛行士は、任意の方角の等距離に宇宙の地平面（宇宙の

果て）を認め、任意の方向の宇宙の地平面に向けて宇宙旅行を行い、その地点に

辿り着くと、その地点の任意の方角の等距離に新たな宇宙の地平面を認める事と

なり、更にひたすら同じ方向に宇宙旅行を続けると、次々に新しい宇宙の地平面

を認め、最後には、元居た場所に戻ってくる事になる事が推測される。

この様な宇宙の物質の定常的な循環を可能とする構造こそ、地球の大気の循環の

様に、有限な宇宙を定常な状態に保つ為の必須の条件という事が出来る。

　

ここで、フリードマンの発表と同じ１９８２年には、サーストンの三次元宇宙の

幾何化予想が発表されて、フィールズ賞が授与されているが、ペレリマンがこの

予想を証明する事で、ポアンカレ予想が完全に証明される事となったが、更に、

この奇跡の年には、ドナルドソンが発表した、四次元ユークリッド空間には他の

次元には無い無数の微分構造が存在するというドナルドソンの定理の発見があり、

この功績によりフィールズ賞が授与されている。

ドナルドソンの定理が、物理学的にどの様な意味があるのかという事は、現在ま

で不明（余り検討された事が無かった！？）であるが、距離が非線形に変化する

性質を有する（非線形距離の概念）という事柄が正に該当するものと考えている。

（幾何学による綿密な検証が必要。）

距離は、古来から加減乗除という四則演算が可能な線形の物理量である事が自明

と解釈さられて来たが、非線形の物理量と仮定すれば、一挙に多くの天体現象を

簡単に説明する事が出来る様になるものと予想している。

　

ここで、非線形速度の概念について簡単にその要点を説明する事とする。

速度は最大値である光速ｃを持ち、任意の慣性系に於いて、物質中で最高の速度

で運動している光の速さが一定値ｃとして観測されるという驚くべき性質を有し

ている。

この事から、物質の速度の加算が最大速度である光速cに近づくに連れて、頭打ち

になる性質を有している事が解る。

この性質こそ、速度が非線形に変化する物理量である事を表している事になる。

そこで、この非線形の物理量の性質としては、最大値ｃを持ち、この最大値であ

る光の速さは、任意の慣性系で一定の値ｃとして観測されなければならない事が

論理的に導かれる。

尚、速度が相対的な物理量である事は自明で何の疑問もなく受け入れられている

が、相対的な物理量は非線形の性質を有していなければならないという事であり、

非線形の物理量は最大値を有しなければならない事となり、相対的な物理量であ

るにも拘わらず、速度の最大値である光の速さが常にｃとして観測されなければ

ならないという、一見すると逆説的な現象が生じる事になる。

この非線形速度の概念を導入すれば、慣性系の座標変換に於いて、待望の時間と

空間を不変に保つことが可能となる。

　

そこで、距離が非線形の物理量と仮定すれば、非線形速度の概念に習い、距離の

最大値が存在する事となり、それが宇宙の地平面までの距離、つまり宇宙の半径

となり、その最大値に近づくに連れて、距離の加算が頭打ち状態になるという事

で、遠くの距離（空間）ほど収縮している事となり、遠くの天体から発した光が

宇宙空間を伝播するに連れて空間が静的に膨張する結果、その波長が引き延ばさ

れる事となるが、これこそが、ハッブルが１９２９年に発表した、遠くの天体の

光ほど、その赤方偏移率が増加して観測されるという、天文学史上最大の発見を、

実際に宇宙空間が動的に膨張すると考える膨張宇宙論（ビッグバン宇宙論）とは

全く異なる理由により説明できる事になる。

そこで、宇宙の動的な膨張という極めて難解な命題に挑む必要は無くなり、専ら

定常な宇宙の構造を考える事で十分となる。

　

そこで、距離は非線形の物理量に特有の相対的な物理量という事で、四次元超球

の表面に於ける宇宙飛行士の体験を実現する事が可能となり、宇宙原理（宇宙に

中心となるべき特別な構造は無い）や2.7ｋのマイクロ波の宇宙背景放射の極めて

均一な電磁波の強度の理由を容易に説明する事が出来ると考えている。

非ユークリッド幾何学を利用して宇宙の空間の曲がりを確定して、宇宙の構造を

推定しようとの試みがあるが、これは空間の曲がりという絶対的な空間の変化を

表現する物理量を利用する方法である。

尤も、重力現象は、LeSage（ル・サージュ）の重力理論で完結すると考えると、

質量による空間の歪みが重力現象を生じさせていると考えるアインシュタインの

重力理論は必要では無くなり、空間の歪みの概念も不必要となり、宇宙は空間の

曲がりが無いユークリッド空間を専ら研究する事で十分となる。

そこで、ユークリッド空間に非線形距離の概念を導入する事で、距離が相対的な

物理量であるが故に、宇宙に特別な構造は無いという静的な状態を示す宇宙原理

が成立する事を支持する結果となり、更に、非線形の物理量である非線形速度の

概念に支えられている、宇宙には特別な慣性系は存在しないという動的な状態を

示す相対性原理と合わせて、この２つの宇宙の相対的な性質を現す基本原理に基

づいて、宇宙は恒常性を巧妙に保つ事が出来ているという解釈が出来る。

また、このペアの原理は、我々がこれ以上に創造の神の座に近づく術を論理的に

拒否する役目も担った原理という事も出来る。

　

四次元超球の表面が我々が感知可能な三次元の宇宙空間という事がほぼ確定した

と考えると、次の問題は、四次元の性質が三次元に及んでいる現象は何かという

事になるが、四次元ユークリッド空間に於ける空間を構成している距離が非線形

の性質を帯びている事と解釈する事が出来る。

つまり、四次元空間が非線形距離の概念により構成されていれば、四次元超空の

表面である我々が感知できる三次元の宇宙も当然ながら、非線形距離の性質が現

れる現象が観測されるべきであり、この実例がハッブルが発見した遠くの天体程

その光の赤方偏移が増加して観測されるという天体現象であり、任意の方向から

の宇宙背景放射の強度の変動が極めて少ないという観測事実であり、任意の位置

に於ける任意の方角の等距離に宇宙の地平面を認めるという宇宙原理を支持する

結果という事になる。

更に、非線形距離の性質が表出しているこの３次元の宇宙を観測する事で、新た

な観測結果が得られる事になれば、四次元空間の正しい構造が推測される事にな

るかもしれない。

宇宙の直径である四次元超球の直径は、非線形距離の性質を定量化する課程に於

いて、非線形距離の最大値（非線形の物理量である速度の最大値である光速ｃに

対応）は必要な因子であるが、これまでに膨大な観測データが蓄積されている遠

くの天体の距離に比例する赤方偏移率の推移をプロットする事で、その予想され

る赤方偏移率の最大値に対応する距離が距離の最大値である四次元超球の半径を

表す事になるものと考える。

　

ここで、一つの興味ある疑問として、四次元超球という宇宙の構造が存在してお

り、四次元故に距離が非線形（ドナルドソンの定理）になったのか、それとも、

宇宙に余剰次元など無く、元々、三次元空間しか存在せず、距離が元々非線形の

性質を有している為に、四次元超球と同等な宇宙の環境（擬似的な四次元超球）

が生じているのか、という事である。

これは、非線形距離の概念を導入した新しい幾何学を用いて決着されるものと考

える。

　

これからは、数学を主導の元に、更なる宇宙の四次元構造を解明する事により、

願わくば、新しい宇宙旅行の航法が開発されて、現行の理論では不可能と考えら

れている遙か彼方の宇宙人が住む天体に往来できる様な胸躍る未来への夢を膨ら

ませたいと考える次第である。

その為には、先ずは、非線形の数をダイレクトに扱える非線形代数学（仮称）の

創設が必要であり、これを利用した非線形幾何学（仮称）の創設が必要と考える。

　

E節＞相対速度の本質と絶対空間の概念の有用性

　２００２年の４月頃から約半年間、インターネットの或る物理学専用の掲示板

で、光のドップラー効果に於ける不思議な現象が議論された事がある。

これは、観測機器に固定された系で考えると、光速不変性により、光と観測機器

との間の速度差は光速ｃであり、この際の光と観測機器（受光器）との相互作用

時にはドップラー・シフトは生じない事となり、全てのドップラー・シフトは、

光源である遙か遠くの星から光が放たれた時点で星と観測機器との相対速度分の

ドップラー・シフトが生じる事となり、この現象は、光が観測機器と相互作用す

る時点で決定される星と観測機器との間の相対速度の情報が、星から光が放射さ

れる時点で既に決定されていることを意味し、因果律に反する現象ではないかと

言うものであった。

光のドップラー効果を理解する為の身近な例えとして、光速で動いているベルト

コンベアーを想定し、光源から放射される光の１波長分の波を一個の荷物に例え、

ベルトコンベアーのベルト上に荷物を一定の時間間隔で載せたり降ろしたりする

場合を想定し、観測者はベルトコンベアーの機械に固定しているものとする。

ベルトコンベアーに近づいて来る光源の場合はベルトコンベアー上の荷物の距離

の間隔は縮まり、逆にベルトコンベアーから遠ざかる運動をしている光源の場合

は荷物の間隔が広がる事となるが、光の波長が短くなったり長くなったりする事

に対応する。

更に、光を観測する受光機器をベルトコンベアーにより運ばれて来た荷物を拾い

上げる作業に例えると、ベルトコンベアーに近づきながら荷物を拾い上げる場合

は、拾い上げる時間間隔が短くなり、逆に遠ざかる運動の場合は、時間間隔が長

くなる事となるが、光の波の周波数の周期が短くなったり長くなったりする事に

相当する。

ドップラー現象の怪は、観測者が観測機器即ち荷物を拾い上げる装置に固定され

た系に居て観測する場合に、光速不変の原理にて、ベルトコンベアーと観測機器

との相対速度が光速ｃのままであり、この際にドップラー・シフトが生じる事は

無く、ベルトコンベアーと観測機器との速度差の光速からの変位分が、光源から

放射された光がベルトコンベアーに乗せられる際に光源とベルトコンベアーとの

速度差の光速からの変位分に恰も予め上載せられた状態で観測される様に生じる

大変不思議な現象である。

　そこで、一つの解決策として、現在では無用の長物と考えられている絶対空間

（絶対静止系）の概念を利用するという考えを提案した。

この眼目は、光や質量を有する全ての物質は、絶対空間を基準にして、絶対的な

速度を有し、光は絶対空間に対し常に光速ｃで運動し、その他の物質も光速以下

の或る絶対速度で運動していると仮定する事である。

この様に仮定すると、星から光が放たれる時点で、光の絶対速度と星の絶対速度

の間の速度差の光速からの変位分に応じた絶対的なドップラー・シフトが生じ、

この光が宇宙空間を極めて安定した状態で伝播し、観測機器と相互作用を生じる

際には、光の絶対速度と観測機器の絶対速度との間の速度差の光速からの変位分

に応じた絶対的なドップラー・シフトが生じ、結果として、これまでの２カ所で

の絶対的なドップラー・シフトが合成されたシフト幅（結果的には、絶対速度の

成分は打ち消されて、観測した光源と観測機器との相対速度のみに依存）を観測

する事となる。

つまり、絶対静止系を想定して、絶対速度に依る絶対的現象をシミュレーション

しても、相対性原理に反する現象とはならない事を再確認したい。

そこで、絶対空間の概念を導入すれば相対的な現象と考えられている多くの現象

が実際は絶対的に生じているが、我々はその絶対的な現象を観測する術が無く、

相対的にしか観測し得ない為に、一見すると因果律に反する様な現象を生じてい

る様に錯覚されるというものである。

つまり、観測機器に固定された系で考えた場合の光のドップラー効果は、勿論、

実際に光源のみで全てのドップラー・シフトが決定されている訳では無く、これ

はあくまで見かけの現象であり、光が光源から放射される時点では、観測機器の

運動状態とは無関係に、絶対空間を基準とした光源の速度に応じたドップラー・

シフトを生じて宇宙空間を伝播している訳であるが、その状態を観測する術が無

いという事になる訳であり、光と観測機器との間での相互作用時にも、論理的に

は全くドップラー・シフトが生じない様に観測される事にはなるが、この現象も

相対的に生じるいわば見かけの現象であり、実際は絶対空間に於ける観測機器の

速度に応じて絶対的なドップラー・シフトが生じていると言う事になる。

　

又、別の解決策として、光が光源から放たれる際に、光源（電子）との相互作用

により、光と光源との相対速度に関する情報を光自身が獲得し、宇宙空間を伝播

して観測機器との相互作用を生じる時点に獲得される情報とが合わされて、初め

て光源と観測機器との相対速度分の確定されたドップラー・シフトを生じる事に

なるという、或る意味では、量子の持つ物理量が観測される迄は不確定な重ね合

わせの物理量の状態であるという考えと同様な考えも提案された。

しかし、それでは、光源から放たれた光は光源の運動状態を表す何らかの情報を

何らかの方法で光自身が保持しておかなければならない事となり、しかも不確定

な周波数のままで、宇宙空間を伝播して行くという、これまた量子力学の特有な

量子の大変不思議な状態と同様な状態を想定しなければならなくなるという欠点

を生じる事となるが、絶対空間を想定する事で不確定な物理量を持った状態など

考慮する必要も無くなる事になる。

なお、余談であるが、観測者から観て光源が静止していても、光源の本体である

原子に捕捉されている電子は猛烈な速度で原子核の周囲を周回している事から、

本来は、光を放射する電子の周回速度分のドップラー・シフトが加味されなけれ

ばならない事となるが、任意の原子を周回している電子の周回速度がほぼ一定と

いう暗黙の前提がある為に、静止光源の光のスペクトルを基準にして、運動中の

光源からの光のスペクトルがどの位シフトしているかという相対的な偏移のみが

問題となる為に、光源の電子の周回速度は考慮する必要が無いという事になる。

　

　量子力学の大変奇妙な量子の性質として、観測（他の物質との相互作用）され

て初めて量子の持つ或る基本的な物理量が確定する（波束の収縮）という事が、

一般的に信じられている。

これに関する最も有名な議論として、実在主義のアインシュタイン等と実証主義

のボーア（コペンハーゲン派のボス）との間で繰り広げられたＥＰＲ論争がある。

これは、不確定な物理量など存在しないと考えるアインシュタイン等が、現在の

量子力学に未発見である物質に備わっている隠れた変数が存在する事を仮定する

事によって、不確定な物理量の概念は不要となるという考えである。

現在では、局所的な隠れた変数が存在する場合のベルの不等式の理論及び、この

理論の破れを実際に確かめたアスペらの実験により、アインシュタイン等の考え

（局所的な隠れた変数理論）が否定された事で決着がついた事になっている。

しかし、遠く離れた量子同士の不確定な物理量が一方の量子を観測した時点で、

瞬時に決定されるという大変奇妙な結果を生じている事を許容する結果ともなっ

ている。

アインシュタイン等は、これこそ物理学的にはあり得ない矛盾した結果を生じて

いる為に、観測する迄は量子の物理量は確定しないとする量子力学の主流の解釈

は間違っていると主張している訳であるが、極めて常識的な判断と言えよう。

そこで、ボームの量子ポテンシャルの概念を導入した新しい量子力学では、この

非局所的な相関の問題を解決する為の非局所的な隠れた変数理論を提案している。

　

ところで、この様な量子が持つ不確定な物理量の状態を想定する事は、量子力学

の最も神髄の概念に関する事柄であるが、例の如く絶対空間の概念を適用すると、

我々は原理的に相対的な現象しか測定不可能であり、量子を観測する迄は不確定

と考えられている物理量も、隠れた変数理論の考えを導入する必要もなく、実際

は確定した物理量として取り扱うことが出来る可能性を今後検討する価値がある

ものと考える。

その為に、絶対空間の存在を仮定した新しい自然観に基づく新しい局所的な隠れ

た変数としての絶対的な現象の存在を仮定した場合のベルの不等式の成立過程に

於ける論理の展開を再検討する必要が有ると考える。

その為には、光子や電子の量子に素光子又は素量子をラベルする仮想的な実験に

依り、それぞれの量子を区別する事が出来るとする考えを導入する意義も検討に

値すると考える。

　

局所的な隠れた変数の考えは、光や物質の絶対空間との関わり合いで実際は確定

している絶対的な現象が存在するが、我々は相対的な現象しか観測する術を持た

ない為に、相互作用（相対的な現象！）する迄は不確定な重ね合わせの状態と考

えざるを得ないという解釈と本質的には同じ概念ではないかと考える。

つまり、隠れた変数とは絶対的な現象に於ける物理量の事であり、相対的な現象

である相互作用が生じる時点で相対的な観測値が得られるという事であり、相互

作用が生じて初めて相対的な観測が決定されるという事で、或る意味、観測され

る迄は全ての取り得る可能性のある不確定な物理量の重ね合わせの状態にあると

いう解釈も出来るという事ではないかとの推測である。（巻末の参考文献（Ｎ）

；アインシュタインのボルンへの往復書簡での”神はサイコロを振らない”）

今回、光のドップラー効果を例として、光（光子）を含めた量子の不確定な重ね

合わせの状態という量子力学の不可解な解釈に対する現行の理論には無い新しい

解決策を提案した。

　

果たして、絶対空間なるものが本当に存在するのかどうかは、相対性原理が完全

に正しいとすれば、それを検証する術は無い事になるが、これからは、論理的に

その存在の妥当性が更に見い出されて来る事を期待したい。

尚、絶対静止系の考えの最大の欠点と思われる事柄は、これが新たなエーテルの

概念を仮定する事に等しいというジレンマを生じる事となるのではないかという

事である。

光や質量を有する物質は決して如何なる媒質としてのエーテルを介して伝播する

訳では無いが、絶対空間を想定する事自体が絶対運動（絶対速度）を想定する事

を意味しマイケルソン・モーレーの電磁波の媒質としての古典的エーテルと地球

の速度差を検出しようとした実験が、意に反しエーテルの存在を否定した事と同

じ様な困難に直面する可能性があるからである。

但し、媒質としての如何なるエーテルの存在も否定されて然るべきではあるが、

その為には、空間に物質に及ぼす如何なる物理的性質を付加する事も許されず、

光を含めた全ての物質が絶対静止系に於いて絶対速度で絶対運動を行っていると

いう想定に依る新たな相対性原理の問題に対処する事が必要であり、これを解決

する手段として、新しい相対性原理を基にした「物質の運動の頭打ち現象」即ち、

非線形の速度の概念が必要となるものと考えている。

　

なお、人間の基本的で素朴な感情としては、本質的で絶対的な基本法則を拠り所

としたい（科学とは絶対的な物の理の探究）という願望がある事も確かであろう。

例えば、全方位からの2.7ｋの宇宙マイクロ波背景放射のドップラー効果が等しく

観測される慣性系をもって宇宙の絶対静止系の候補とする考えもある。

これは、何故宇宙が存在するのかという物理学の範疇を超えた哲学の究極の命題

に近づく長い階段の１ステップでもある。

尚、この全方位に渡り１０^-5以下の揺らぎしかない極めて均等な宇宙マイクロ波

背景放射の起源として、ビッグバン宇宙理論ではビッグバン初期の残光であると

の解釈を行っているが、宇宙の全空間を満たしている自由素光子場の固有振動の

さざ波を観測している可能性も検討に値するものと考える。

又、エネルギーが重力源となる事が証明されているので、運動エネルギーのみを

有する自由素光子場も有意な重力源に成り得る事となり、ダーク・マターの有力

な候補にも成り得るのではないかと考える。

因みに、量子色力学でその存在を予言されているアクシオン（アキシオン）は、

推定の質量が電子の１０^-12倍程度であり、ダーク・マターの有力な候補と考え

られているが、強力な磁場中では電磁波として観測されると予想されている。

尚、素光子の質量は電子質量の約１０^-20倍であり、ニュートリノの質量は電子

の質量の２×１０^-5倍以下である。

　

光の速度は、任意の慣性系に於いて常に最高速度ｃという一定の速度として観測

される（光速不変の原理）が、大変不思議な現象と言わざるを得ない。

古来より自明と考えられてきた速度の線形性を非線形性に変更する事は、無限大

まで許容される線形の性質を有する速度を、ギューッと押し縮めて有限の速度ｃ

を極限値として光速ｃに近づくに連れてその速度の増加する割合が限りなく減少

する様な非線形に変化する性質の速度に変更する事と同等ではないかと考える。

光速ｃは数学的には有限の値ではあるが、無限のエネルギーで物質を加速しても

到達不能な、いわば物理的には無限大の速度に相当する速度と考える事が出来る。

つまり、数学上の線形の最大の速度である無限大（∞）の速度の概念の元では、

任意の速度ｖの慣性系に於ける最大の速度が、∞±ｖ⇒∞となり、常に∞として

観測される事（ニュートン力学に於ける光速不変の原理）に対応して、自然界の

非線形の速度の極限値としての光速ｃの概念の元では、任意の速度ｖの慣性系に

於ける最大の速度がｃ±ｖ⇒ｃとなり、常にｃとして観測される事になるものと

考える。

つまり、光と質量を有する物質との間の相対速度を観測する場合は、物質がどの

様な慣性運動を行っていようとも、物質から光を観た場合は、光の速度がｃ±ｖ

⇒ｃとなる様に観測される事になり、光から物質を観測した場合は、物質の速度

が±ｖ⇒０となる様に観測されるという事になり、慣性運動中の全ての質量を有

する物質は、或る慣性系（代表して絶対静止系）に静止した状態と同等となり、

任意の慣性系に於ける光と物質との相互作用時に、光が物質に等しい力を与える

事を意味する訳であり、森羅万象が質量がゼロの光と質量を有する物質との相互

作用により生じる事を考慮すると、任意の慣性系の物理現象が対等に生じる事を

要請する相対性原理が成立する為の自然の持つ巧妙で基本的な仕組みである事が

分かる。

ところで、速度ｖの慣性系から観測した光の速度が、ｃ±ｖ⇒ｃとして、正確に

ｃという値をとるのか、又は、近似的にｃという値として観測されるのかという

素朴な疑問も生じる。

　ニュートン力学の絶対空間という自然観に依れば、光は絶対空間を絶対速度ｃ

で伝播する事となり、質量を有する全ての物質は、絶対空間を光速より遅い或る

絶対速度ｖで運動している事となるが、相対性原理が正しいとすれば、絶対空間

を特定する事は論理的に不可能となり、観測可能な全ての現象は相対空間に於け

る相対的な速度を基にした相対的な現象という事になる。

そうすると、加速器で加速して光速に限りなく近づいた電子からの制動輻射光の

速度を測定した実験でも、光の速度は正確に光速ｃとして観測されているという

事実から、光の伝播する速度は、矢張り数学上の無限大の速度（任意の慣性系で

常に瞬間的に伝わる無限大の速度として観測される）と同じく常に一定の速度ｃ

で伝播する性質を有していると判定しても良いと考える。

更に、光速ｃより極僅かに遅い速度で運動している光があるとすると、この光の

質量も最早ゼロでは無くなり、質量を有する物質も光速ｃに限りなく近い速度を

取り得る事を考えると、両者の本質的な違いが無くなり、任意の慣性系に於ける

光と質量を有する物質との相互作用である物理現象が等しく生じる事を要請する

相対性原理に反する物理現象が生じる事となる。

　光のドップラー効果に関する奇妙な例として、観測者が観測機器に固定された

系の場合は、観測する光と観測機器の速度差が光速ｃとなる事に依り、観測機器

に於けるドップラー・シフトは生じることが無く、全てのドップラー・シフトが

恰も光源から光が放射される時点でのみ生じる様に観測されるという、一見する

と因果律に反する様な不可解な現象となるという事であるが、これは光源側で生

じる相対的な現象を絶対的な現象と錯覚する事により生じる事となる。

つまり、絶対空間では、光は絶対速度ｃで運動しており、観測機器に固定した系

も或る絶対速度ｖで運動しているとすれば、光が観測機器に捕捉されて相互作用

する際に、光と観測機器の速度差（ｃ±ｖ）が絶対的な現象としてのドップラー

・シフトを生じさせる因子となるが、観測機器に固定された観測者にとっては、

この絶対速度ｖが相対速度としてゼロとなり、絶対的な現象としてのドップラー

・シフトが生じない（正確には、シフト幅ゼロのドップラー・シフトが生じる）

様に錯覚されるという事になる。

つまり、常に光速ｃという一定の速度で観測される光の速度も、一定という事で

絶対速度の様に錯覚されるが、実際は絶対空間に於ける絶対速度では無く、相対

空間に於ける光の相対速度を観測している事となるが、非線形の速度の性質とし

ての極限の最高速度故に一定の速度ｃとして観測される事になるという事になる。

尚、加速状態の観測機器に於いては、加速方向から来る光の速度は光速ｃを超え

て観測され、一方、逆方向から来た光の速度は光速ｃより低下して観測される事

が実証されているが、光の速度が無限の速度に匹敵する光速ｃから変動する事が

自明の様に語られてはいるが、この性質も考え様によっては、大変不思議な性質

と言わざる得ない。

　ここで、光速不変性を素光子説の立場で考察してみる。

素光子の束縛状態である素量子の運動状態式に於いて、不顕性エネルギーである

素量子の質量エネルギーが全て運動エネルギーになりフル・パワーの状態になっ

たのが、束縛状態から解放された素光子の最高速度ｃでの運動状態という事にな

るが、この現象として、電子や核子からの素光子の集団である光の放射や核変換

による質量欠損分の光の放出や反粒子同士の対消滅時に生じる全エネルギー分の

光への変換等があるが、光は何処からのエネルギーの付加も無く、自ら速やかに

光速ｃという定常の運動状態に達する事となる。

そこで、任意の慣性系で光を観測した場合に、光の質量は常にゼロとして観測さ

れる事により、素光子の不顕性エネルギーである質量エネルギーはゼロとなり、

素光子の持つ固有エネルギー（ｈ／ｓ）の全てが運動エネルギーの状態となり、

素光子が最高速度ｃを維持する事が可能となり、任意の慣性系に於いて光の速度

が光速ｃという一定の速度で観測される事となる。

なお、座標変換に於いて素光子の質量エネルギーがゼロの状態に維持されている

事が、即ち、任意の慣性系に於いて光速が一定の値ｃとして観測されるという事

を意味している事にもなる。

また、極言すれば,非束縛状態の素光子の定常状態は光速ｃでの運動状態であり、

束縛状態にある素量子では、束縛状態故に光速での運動状態になる事は不可能と

なり、光速より遅い速度しか取り得ず、その結果、運動エネルギーが減少して、

その分の不顕性エネルギーである質量エネルギーが増加する事により、質量を有

する物質として観測されることとなるが、その全エネルギー（運動エネルギー＋

質量エネルギー）は不変となると考える。

これで、慣性系に於ける座標変換に於いて、物質の全エネルギーは保存される事

となり、エネルギー保存則が、時間発展のみならず座標変換に於いても成立する

事となる。

なお、我々は動かない物が安定しているとの素朴な想いがあるが、宇宙で最も安

定している物質は、常に最高速度ｃで運動している素光子であるという全く逆の

認識が必要になると考える。

素光子の光速ｃでの定常の運動性こそが、宇宙の創造主の最も自慢したい発明で

はないかと想う次第である。

　

E節＞超常現象

　超常現象と呼ばれている現行の物理学の研究対象から外れている一連の不思議

な現象の存在を肯定的に認めれば、自然現象の範疇の生命現象に深く関わってい

るこの不可解な現象の中核と考えられる俗に念力と呼ばれている未知の力に関し

て考察する事が重要と考える。

　

電子や原子核に捕捉されている半束縛状態の素光子の集団が開放される事が光の

放射と考えると、人体の或る特定の細胞から光とは異なる性質を持った素光子の

集団が放射される可能性が考えられる。

つまり、超常現象の中心的役割を担っていると考えられる念力とは、この様な光

とは多少異なる性質を持った素光子の集団（俗に言う念波相当）と物質との相互

作用により惹起される純粋な力学現象ではないかと考える事が出来る。

光が唯一の受光器である眼球組織でしか受信されない事とは異なり、念力は全て

の細胞がその発生器及び受信器となり得るものと考える。

１つの細胞が発生する念力の強さは極微弱であろうと推測されるが、意識を集中

させて念じることにより、複数の細胞が一斉に同期して同一の方向に念力という

素光子のビームを集中させて発生させる事によって、肉眼的に確認できる現象と

なる事が出来るものと考える。

ところで、生命活動に必要なエネルギーが、細胞内のミトコンドリアと呼ばれて

いる特殊な器官で化学エネルギーとして発生されている事が詳細に研究されてい

るので、この器官が念力の発生源及び受信源の第一候補と考る。

そこで、通信手段として利用されている或る特定の周波数帯域の光は電波と呼ば

れており、振幅変調（ＡＭ）と周波数変調（ＦＭ）に大別されているが、念力の

具体例の一つと考えられる念波（テレパシー等）は、どちらの変調方式により、

又は全く新しい変調方式を利用して情報が伝達されているのであろうか？

一般的な光の発生は原子核に捕捉されている束縛状態の電子が遷移する際の制動

放射であるが、電波の発生は自由電子の加速時の制動放射が主な発生源である。

念力の場合は、電波と同様な機序で、又は全く新しい発生機序で生じているので

あろうか？

ミトコンドリアの膜に存在するＴＣＡサイクルにより発生した化学エネルギーを

利用してエネルギー効率がほぼ100%という理想的な回転運動を行う鞭毛モーター

や直線運動を行う筋肉組織は、最新のマイクロ・マシンを遙かに超える驚くべき

高度に分化した精巧な高分子構造体で形成されている。

この高分子構造体が高速回転運動を行う際に、高分子構造体に属する自由電子か

ら素光子の集団（念波；或る周波数の電磁波）が制動放射として放射される事が、

念力の発生機序ではないかと推測している。

ところで、脳の組織の或る神経細胞内のミトコンドリアの活動が異常に持続して

亢進する場合に躁病が発症し、逆に低下する場合に鬱病が生じるのではないかと

いう研究が最近注目されている。

特に鬱病の最大の問題となる阻止し難い自殺願望（個体のアポトーシス）の症状

に対して、ミトコンドリアの機能の正常化を行う事により症状を改善させようと

する治療薬の開発が期待されているが、念力によりミトコンドリアの働きを正常

にコントロールする事が可能となるかも知れない。

また、細胞内のミトコンドリアがアポトーシス（細胞の自己破壊）を司っている

事が解っている。

癌細胞とは、正常細胞に備わっている必要に応じて起動するアポトーシスという

自爆機能を免れている為に制限無くランダムに増殖を続ける事が出来る細胞とい

う見方が出来るが、ヒーリングによる癌組織の消失という信じ難い現象が本当で

あれば、念力（念波）を受信した癌細胞のミトコンドリアに於いて、失活してい

るアポトーシスの機能が復活する事で癌細胞の消失が達成されているのかも知れ

ない。

なお、癌化とは、成熟した正常細胞が何らかの外的因子にて細胞が幼若化を生じ

る結果生じると最近まで信じられて来たが、最新の研究により、未分化の幹細胞

の段階の細胞分裂の際の紡錘糸の機能不全を引き金とする細胞核の分裂の異常が

原因という説が有力になっている。

つまり、癌細胞を何らかの方法で分化させる事が出来れば、アポトーシスの機能

が発現して死滅させる事が出来る可能性が生じ、転移を起こす機能を持っている

悪性腫瘍を、転移を生じない良性腫瘍に分化させる事が出来る可能性が生じる。

　

空中浮揚という重力に抗する様な大変不思議な現象があるが、これも念力として

の素光子のビームが地面に放射される結果生じる反動（作用に対する反作用）で

説明できるかも知れない。

余談であるが、常温核融合が元来の予想とは異なる意外な現象として再評価され

ているが、ミトコンドリアでもこの現象が未発見の化学反応の形式で達成されて

いる可能性があると考えている。

　

ところで、遠隔移動は、念力だけでは説明できない様に思われる。

これまでの物理実験により確かめられている粒子が消えては現れる現象を説明す

る為に、現在、ＣＥＲＮのLHCにて実証実験が行われているリサ・ランドール教授

の余剰次元の考えが正しいとすれば、遠隔移動とは余剰次元の存在を示唆してい

るのかも知れない。

兎に角、念力という未知の力の存在を想定し、定量的に検出する方法を確立する

事が先決である。

　

E節＞素光子の状態分類

　ここで、全体の纏めとして、素光子の集合状態の違いを大まかに４つに分類し、

森羅万象を巨視的に眺める事で、このレポートの締め括りとしたい。

　

（１）自由素光子場（ゼロ点エネルギー、重力場）

宇宙空間全体に均等に分布して自由に光速で運動している状態の素光子の集団を、

自由素光子場と呼ぶ。

全方位からの素光子の密度が均一の素光子場を、原子レベル以上の質量を有する

物質が他の外力を受けない状態で運動している場合は、素光子の光速不変性及び

運動量不変性にて全方向からの素光子の衝突を概ね均一に受ける為に全方向から

受ける素光子の合力がほぼゼロとなり、これ迄の運動状態を強いられる事となり、

所謂慣性運動（慣性の法則）を行う事となるが、質量が小さい量子のスケールで

は、全方向からの素光子の衝突に多少のムラが生じる事により所謂ジグザグ運動

を行う事となる。

尚、物質に外力が加わり加速が生じれば、加速方向からの素光子の衝突の機会が

増え素光子の速度が光速を超えて衝突時の運動量が増加するが、加速と反対方向

からの素光子の場合はこれと反対の効果をもたらす結果、合力が加速方向からの

抵抗力となり、これを慣性力として観測する事となる。

　

また、素光子をLe Sageの重力理論の宇宙空間に存在するガス状の微粒子の本態と

仮定すると、矛盾なく重力の発生機序を説明できるものと考える。

更に,銀河を構成する天体の円盤状の回転運動を生じさせる機序として、Le Sage

の重力理論に於いて、銀河等の宇宙の中規模のスケールに於いては距離の逆二乗

に比例するとする現行の重力理論では無く、重力が距離の逆数に比例する可能性

を挙げたい。

それから、ミクロの現象に於ける量子力学のゼロ点エネルギーは、自由素光子場

その物の効果であり、量子の加速度運動時に抵抗力を生じさせる結果、古典粒子

には想定外の奇妙な振る舞いの原因となる現象を生じさせているものと考える。

つまり、現行の量子力学の解釈である量子の振る舞いは、量子の基本的な性質の

現れでは無く、古典粒子が自由素光子場から受ける抵抗力によって生じる二次的

な現象では無いかと推測する。

　

ハミルトニアンＨが、粒子の運動エネルギーとポテンシャル・エネルギーの和と

して、粒子の運動状態の解析に汎用されているが、ポテンシャル・エネルギーは、

具体的には、重力場の勾配差のエネルギー量や電場の電位差のエネルギー量を表

している訳であるが、素光子説の立場で言えば、共に素光子の密度の差に帰着さ

れる事になり、更に宇宙空間に均等に分布している自由素光子場をポテンシャル

・エネルギーの概念に加えると、全ての場での粒子の振る舞いを統一的に記述す

る事が可能となるものと考える。

デイビット・ボームが提唱する量子ポテンシャルは、零点エネルギーに相当し、

ド・ブロイが発案しボームが量子ポテンシャル理論にて発展させた量子が携える

パイロット波とは、正に古典力学に従う粒子（古典粒子）が加速度運動を行う際

に自由素光子場から受ける抵抗（ジグザグ運動等の量子効果）を表現していると

考えると、ＥＰＲ論争に於けるアスペらのベルの不等式の破れの証明も、局所的

な隠れた変数の理論を否定するものとは言えず、量子効果を証明したものに過ぎ

ないのかも知れない。

　

なお、確率過程論の研究者である長澤正雄博士は、１９９７年にベルの不等式の

論理的な間違いを指摘した論文を発表している。（巻末の文献Ｈのｐ１２１）

更に、量子の運動が確率的であり決定論的な予測が出来ず、一見すると観測され

る迄は不確定な物理量と解釈されている量子の持つ物理量の奇妙な性質も、古典

粒子が素光子場から受ける二次的な効果により修飾された結果を観測しているに

過ぎないものと考えられる。

　

ここで、宇宙規模の観点から素光子一元説を考える。

先ず、宇宙空間に、自由に光速で運動している素光子の集団（自由素光子場）が、

或る均等な密度で充満している状態を想定する。

この自由素光子場は、現行の理論に於ける零点エネルギーや真空のエネルギーに

相当する。

ここで、この宇宙空間の任意の慣性系に１つの物体が存在すれば、物体の周囲で

運動中の素光子は、光速不変の原理により、全て常に光速ｃで運動している事と

なり、これらの素光子が物体に衝突する場合には、周囲の素光子場の密度が均等

である事から、周囲の素光子の衝突（素光子圧）も均等となり、素光子の衝突に

より物体に加えられる合力はゼロとなり、加速運動を生じる事は無い。

つまり、慣性運動とは他の力が働かない状態に於ける物体の運動状態の事である

が、周囲から力が加えられている場合でも合力がゼロの状態であれば、物体に全

く外力が加えられていない状態と同等に慣性運動状態として観測される事となる。

ただし、ミクロの状態を観れば、無限小では無い有限の運動エネルギーを持った

有限個の素光子が衝突する事で、正確に合力ゼロとはならず、この合力の時間的

な変動が所謂、量子力学で言う”ゆらぎ”として観測される事となり、この合力

の変動である”ゆらぎ”を生じるエネルギーの最小単位が、１個の素光子の運動

エネルギーε（ｈ／ｓ）という事になる。

なお、物体に外力を加えて加速状態になれば、加速方向からの衝突する素光子の

速度が光速ｃを越える事となり、その分、素光子の運動エネルギーが増加する事

となるが、反対に、逆方向からの素光子の速度が光速ｃより低下する事となり、

その分、素光子の運動エネルギーが減少する結果、この合力は加速方向から物体

の加速度を低下させる方向に抵抗力として生じる事となり、これが所謂、慣性力

という事になる。

電磁場（荷電粒子に捕捉されて周囲を拘束ｃで運動中の半束縛状態の素光子場）

は、ゲージ原理（任意の空間の各点で独立な変換を行っても物理法則は変わらな

い。）の最も基本的な適用の場であるが、自由素光子場もゲージ原理を問題なく

適用される場と考える。　

　

ここで、この宇宙空間に２つの物体が存在すれば、各々の物体による自由素光子

の運動が遮蔽される事により、物体間の空間の自由素光子場の密度が低下する事

が予想されるが、密度の低下率は２つの物体の質量の積に比例し、物体間の距離

の２乗に逆比例する事が予想される。

すると、各々の物体には、自由素光子場の密度の低下の割合に逆比例する合力が

物体同士を近づける方向に働く事となり、これが重力の発生機序という事になる。

この考えの原型が、１８世紀の中頃に発表されたル・サージュの重力理論である。

この重力理論は、物体の質量の積に単調（線形）に比例して物体間の自由素光子

場の密度が低下する訳では無く、質量の増加に連れて遮蔽率が１００％に漸近す

る事となり、遮蔽率が１００％、つまり物体を通過する自由素光子がゼロになっ

た時が重力が最大となり、この値は宇宙空間に均等に分布している自由素光子場

の密度に依り決定される。

この点が、ニュートンの万有引力の法則やアインシュタインの重力理論等の現行

の重力理論との大きな相違点であり、光（自由素光子の集団）すら脱出不可能な

ブラック・ホールが生じる可能性は無い事となる。

また、２つの物体間の自由素光子場の密度に関係する因子として、物体間の距離

がある。

一見すると、各々の物体に働く合力の強さは電磁気力（クーロン力）や他の重力

理論の様に距離の逆２乗則に従う様に思われるが、決して単純では無い。

分子間に働く引力であるファンデルワールス力が距離の６乗に逆比例する事実が

有るが、ル・サージュの重力理論に於ける重力がこの分子間力の本態と仮定すれ

ば、分子間の距離のスケールでは、物体間の距離の６乗に逆比例する重力が働く

という事が推測できる。

又、微小な平行板の間には距離の４乗に逆比例する引力が働くというカシミール

効果があるが、これこそ、この距離のスケールに於けるル・サージュの重力理論

に基づく重力が働いている現象であると推測される。

また、微生物から太陽系までのスケールでは、所謂、距離の逆２乗則に従う重力

が働くのではないかと推測される。

更に、銀河のスケールでは、距離の１乗に逆比例する事が予想される事となり、

この効果が、ダークマターの存在を必要としている銀河の回転曲線の平坦化を生

じたり、パイオニア・アノマリーを生じているのではないかと推測される。

さらに、このスケールを越えると、距離の逆０乗に比例、つまり距離に関係なく

一定の重力が働く事になるのではないかと推測する。

　

速度の概念を現行の線形性から非線形性に変更する事で、時間と空間を普遍に保

つ事が可能な新しい慣性系の座標変換を提案しているが、距離の概念も相対的な

非線形性に変更する事で、ハッブルが発見した天体迄の距離に比例した赤方偏移

を生じる現象を、現行の膨張宇宙論とは異なる定常宇宙論の範疇で説明が可能な

事を見出している。

又、非線形の速度の最大値である光速ｃに対応する非線形の距離の最大値は宇宙

の半径（任意の観測地点から宇宙の地平面迄の距離）という事になり、宇宙原理

を保証する全く新しいタイプの定常有限宇宙論を構築する事が可能と考えている。

尚、宇宙が４次元（３次元＋余剰次元）の構造体であると推定しているが、距離

の非線形性は余剰次元の性質の表れではないかと考える。

空間の曲がりが無い４次元のユークリッド空間を研究する幾何学の検討により、

距離の非線形性の性質が必然的に導出されるかも知れない。

これを示唆する幾何学の成果として、１９８２年のドナルドソンの定理がある。

四次元ユークリッド空間が、正しい宇宙の構造という事になれば、四次元超球の

表面の性質として、地上の旅人がいずれは元居た場所に戻る現象と同様に、有限

ではあるが果てのない宇宙構造を達成する事が可能となり、宇宙の構造としての

希望的な予測である有限定常宇宙論が現実味を帯びて来る事となる。

これは、宇宙空間に存在する自由素光子場が均等に分布して定常状態を保つ為に

は、自由素光子場の構成要素である素光子が任意の方向に光速で運動して宇宙を

一周して、いずれは元居た場所に戻るという定常に循環状態保つ事を可能とする

宇宙構造が必要であるという要請をクリアー出来るものと考える。

　

究極の理論の条件として、”指導原理から一意的に理論が決まること、基本粒子

や基本的なパラメータの数ができる限り少ないこと、 パラメータの間の微調整が

ないこと、 重力が矛盾なく記述されていること”が一般的に述べられているが、

素光子説（素光子一元説）は、十分な条件を有しているものと自負している。

　

（２）自由素光子の集団の規則的な運動状態（電磁波、光子）

光（モデルとしての電磁波や光子）として観測される。（巻末の図２参照）

Unruh効果は、真空中に置いた電磁波の検出器を或る振動数で振動させると、その

振動数の電磁波を検出するという不思議な現象であるが、何もないと思われてい

る真空中には自由素光子場が存在する事を考えると、検出器が相対的に電磁波を

観測する事は至極当然の事であり、Unruh効果こそが自由素光子場の存在を間接的

に実証している現象であり、更に、電磁波（光子）が自由素光子の集団である事

も実証している現象と考える。

更に、自由素光子場の存在が間接的に実証されている事は、Le Sageの重力理論の

根拠が間接的に実証されている事でもある。

　

（３）半束縛状態の素光子（電磁場）

荷電粒子に捕捉されて、周囲を光速ｃで旋回している素光子であり、荷電粒子の

周囲に電場を形成しているベクトル・ポテンシャルそのものである。

現行の電荷のモデルの正負の性質は、荷電粒子に備わった固有の性質と仮定して

いる為に、荷電粒子の自転に起因するスピン角運動量の回転方向に依って変わる

荷電粒子の表面の電荷の回転に起因するスピン磁気モーメントの方向の逆転にも

拘わらず一定を保っている事になっているが、荷電粒子に捕捉されてその周囲を

周回している素光子の運動そのものがスピン磁気モーメントを生じ且つ荷電粒子

間の引力及び斥力を生じる原因と考えると、同種の荷電粒子間でもスピンの向き

が異なる場合は引力が生じ、スピンの向きが同じ場合は逆に引力が生じる事とな

り、電子間の引力によるクーパー対の形成や核子間の引力（強い力）の発生機序

を容易に説明できる可能性がある。

ベクトル・ポテンシャルの数学モデルとしての調和振動子は、単振動という直線

運動であるが、元来は回転運動のモデルが必要と考える。

なお、調和振動子の単振動は、回転運動を側面から観測している状態に相当する

という考えもある。

このモデルにより、素光子（ベクトル・ポテンシャル）の渦を巻く性質の解明が

可能となるかも知れないが、単一の素光子のみで多種多様な森羅万象を演出可能

としている鍵は、この素光子の回転運動が握っている事は間違いないと考える。

　

（４）束縛状態の素光子（素量子の集合体である質量を有する物質）

自由素光子の規則的な集団（光）同士が或る条件の元で出会うと、素光子同士が

絡み合って束縛状態となり、例えば、質量を有する電子と陽電子等の反粒子同士

の対生成が生じる。

これは、渦巻き文様である日本の陰陽勾玉巴を連想させる。

更に、電子や核子に素光子が一旦吸収されるが速やかに放出される場合も、極短

い時間の間、素光子が緩い束縛状態の素量子になっている事が推測される。

素光子同士が束縛状態になる力は、素光子の定常状態である光速での運動状態に

復帰しようとする復元力の存在を仮定する事で説明可能と推測しているが、この

復元力は、ベクトル・ポテンシャル(素光子)の数学的なモデルである調和振動子

のバネの性質である復元力を検討する事により、所謂、弱い力や強い力を説明で

きる様になるのではないかと考える。

なお、質量を持った全ての物質である束縛状態の素光子（素量子）の集合体は、

水（H2O）に例えると氷に相当するが液体の状態は無く、つまり、物質の速度に拘

わらず、束縛状態の素量子間の力関係は一定であり、氷の分子間の結合が離れた

水蒸気の状態になる昇華という現象が、束縛状態の素量子が解放されて素光子の

状態に戻る質量欠損（反粒子同士の対消滅等）の現象に対応すると考える。

　

E節＞素光子説に基づく自然観（素光子一元説）

量子のエネルギー不変の原理を仮定し質量を有する全ての物質を素量子の集合体

と仮定すると、物質にエネルギーを与えて加速する場合に到達する速度が光速に

近づくに連れて頭打ちになる現象が存在する事が論理的に証明されるが、加速器

での素粒子の加速実験でこの現象が実証されている事により、全ての物質を基本

粒子の集合体とする基本的な考えが実証されたものと考える。

物質の運動の頭打ち現象を現行の理論に適用する際に、古来より線形の物理量と

考えられてきた速度を非線形の物理量に変更する事により、慣性系間の座標変換

に於いて時間と空間を不変に保つことが可能となる。

又、相対的な物理量である距離の概念も速度と同様に非線形に変更する事により、

全宇宙規模の天体現象を現行の理論よりも簡単で統一的に説明できる事となる。

　

　自然界の振る舞いの全てをシンプルな方程式で表す事が、理論物理学の究極の

目的とすれば、先ず第一に検討すべき課題は、量子力学が暗に要請している基本

粒子（素光子やその束縛状態の素量子）の基本的な性質であろう。

何故ならば、全ての物質は基本粒子の集合体であり、基本粒子の性質が直接又は

修飾された状態で、その振る舞いの目安である物質の物理量及び運動方程式の全

てに一様に反映していると思われるからである。

この事柄は、物質の運動に関する全ての法則が、万物に一様に適用できる本質的

な原因として、所謂、自然界の空間の基本性質に起因しているとする気休め的な

現行の物理概念に対して、自然の法則の一様性を最もシンプルに説明できる唯一

の手段と考える。

なお、速度の非線形性の概念も、全ての物質が素光子の束縛状態である素量子の

集合体であるとの見地に立てば、全ての物質が光速以下でしか運動できない事は

自明の事となり、光速を極限値とする「物質の運動の頭打ち現象」を、非線形に

変化する速度という物理量で表現したものであると考える事が出来る。

この結果、特殊相対性理論にて相対的な物理量に格下げとなっていた時間と空間

の不思議な現象を想定する必要も無くなり、元来の普遍的な物理量の地位に復帰

する事が可能となると考える。

なお、温度の概念と同様に、速度を集団の運動状態の複合的で統計的な物理量と

解釈すれば、非線形速度を非線形の数として取り扱う必要は無く、現行の数学の

範疇で対応できる事となると考える。

更に、相対的な物理量として非線形距離の概念を導入すれば、ハッブルの法則を

満足する静的な宇宙の膨張を導くことが可能となり、これ迄の天体の観測結果を

極めてシンプルに説明出来る様になると考えるが、高次元の宇宙の構造を推測す

る手掛かりになるものと予想する。

目下のところ、非線形距離は非線形速度の様な複合的な物理量ではなく、基本的

な物理量と考える事が妥当と考えられる為に、非線形数として取り扱う事が可能

となる非線形代数学なる新しい数学の分野の創設が必要となるかも知れない。

ところで、宇宙空間に非線形距離の概念の性質を課す事は、宇宙空間を文字通り

の空虚な隙間という最も単純なモデルから複雑化することであり、空間に関する

解決すべき新たな多くの課題が生じる事となり、幾何学の強力なパワーに期待し

たい。

　

　量子力学に於ける量子の不思議な振る舞いを自然の摂理と解釈せざるを得ない

原因も、現行の量子力学の理論の不完全さから起因しているに違いないと考える。

約一世紀に及ぶ量子力学の膨大な理論体系の大規模な修正を期待したい。

アインシュタインを筆頭に量子力学を不完全な理論と考える有名な実在主義者達

（ド・ブロイ、シュレーディンガー,ディラック,ボーム等）の考えや確率過程論

に加えて、宮沢弘成博士の独自の考えを参考文献として巻末の（Ｌ）に記載する。

　光子や電子やニュートリノ更にはクォークを下部構造を有しない素粒子と解釈

している現行の理論は、これらの素粒子の奇妙な振る舞いを説明する為に、自然

の基本的な不確定性を仮定（不確定性原理）する事で解釈しようと努めてきてい

るが、素光子の存在を仮定する事に依り、不確定性の現れと解釈されてきた全て

の現象が実は素光子との相互作用により惹起されているという事になり、結局、

全ての現象を古典的な現象論で説明する事が可能となり、量子力学の根幹を成す

全ての不確定な要素の概念が不必要となるものと考える。

なお、真の素粒子と位置付けている素光子が不確定な挙動を行うか否かは目下の

所不明であるが、遙か百数十億光年彼方の光が光源から放射された当時の原型を

止めている様に観測される事を考えると、光の構成要素としての素光子が永久的

に極めて安定して一糸乱れない様に協同運動して来た結果と解釈すれば、素光子

の不確定な要素を仮定する必要性は、目下のところ無いと考えている。

　

　素光子は、広大な宇宙という大舞台で完璧なまでの自然の秩序と調和を保って、

壮大で多彩なドラマを、多重人格的な一人何役もの役柄を只ひたすら黙々と熱演

しているのであろうか！？

素光子のみで、この宇宙の森羅万象を全てパーフェクトに説明できるかどうかは、

現在の段階では解らないが、自然界の基本原理は単純であり理解可能な概念であ

る事に違いないとの希望的予測は、我々に共通した生来の素朴で基本的な感情で

あろう。

ここで、素光子説に基づく宇宙創造の荒っぽいシナリオを考えてみる。

創造の神の”光あれ！”という一声にて、宇宙という四次元ユークリッド空間の

四次元超球の表面（三次元ユークリッド空間）に、高密度で膨大な量の素光子の

集団（自由素光子場）が出現して、飽和溶液中の物質の結晶化と同様に、素光子

同士の絡み合いにて自発的に電子や陽子やニュートリノ等の粒子が宇宙の至る所

で連続して生じる事となり、その結果、物質の生成に費やされた素光子場の密度

が或る閾値以下になると、自然に粒子の生成が生じない様になるものと考える。

以上の様に、宇宙の創生期には正粒子だけが生成し、反粒子は生成されなかった

ものと推測している。

つまり、光子同士の正面衝突による正粒子と反粒子の対生成の機会は極めて低く、

粒子の生成の殆どは、高密度の素光子場に於ける自由素光子同士の絡み合いで生

じたものと推測される事となり、現在の宇宙に正粒子のみが存在している理由を

説明する事が出来るものと考える。

尚、素光子同士の絡み合いだけでは安定した物質としての素光子の束縛状態を保

つ事は極めて困難であり、直ちに崩壊する事が予測される為に、物質の周囲から

の素光子圧により自然崩壊が常に阻止されている事が推測される。

従って、物質が生成されて素光子場の密度が或る閾値以下になると、物質の生成

が自然に停止する事になるが、更に素光子場の密度が或る閾値以下に低下すると、

物質の周囲から及ぼされる素光子圧による物質の自然崩壊を阻止する事が出来な

くなり、物質の自然崩壊が始まる事となり、その結果、素光子場の密度が増加す

る事が推測される。

以上の様にして、宇宙空間の自由素光子場の密度は、或る一定の範囲内に自然に

保たれている事が推測される。

なお、高質量の恒星や惑星の中心部では、物質による自由素光子の遮蔽効果にて、

素光子場の密度が星の外部よりも低下している事が推測される事となり、分子や

原子、更には、中性子や陽子や電子が自然崩壊を生じている可能性があり、この

反応が恒星や惑星の内部エネルギー源となっている可能性がある。

なお、素光子説では、ニュートリノは素光子の集団であり、光と同様に質量が無

く光速ｃで運動する性質を有するが、この両者の違いは素光子の集団の構成形態

の違いだけと考えている。

神話や現行の理論では、宇宙の創生期には光（光子や電磁波）のみが先ず存在し、

光子同士の正面衝突にて質量を有する物質が対生成されたものと考えられている

が、素光子説では、電子や陽子等の粒子の加速時や正粒子と反粒子の対消滅時に

しか光やニュートリノが発生しない事となり、光やニュートリノは二次的に生じ

る物質である事となる。

　

全ての自然現象が神の仕業と考えていた神話の時代から、人間の自我の芽生えと

自信の現れとしての自然の探究の結果としての科学の発達に連れて、神の仕業と

科学の間の溝が次第に深まって今日まで到達してきたが、人類の残された好奇心

としての自然の摂理の本質を理解したいという止め難い欲求により、再び、創造

の神の領域への回帰へと向かう必要が出てくるのかもしれない。

もし、自然の摂理としての擬人化した自然の女神を垣間見る事が出来るとすれば、

飾り気のない質素で端正な容姿に違いないと想う。

　

素光子のみでこの様な多様で多彩な宇宙の森羅万象が展開されているという事に

なれば、これだけで誠に驚愕すべきであり、自然に対し畏敬の念を禁じ得ないが、

地球（更には他の多数の天体の惑星）という過酷な自然環境に生物が自然発生し、

ついには人類という知能を獲得した種が進化してきている訳であるが、文字通り

自然の成り行きで偶発的に進化してきていると考えるのか、自然の必然的な流れ

の一環と考えるかは、意見が分かれるところであろう。

人類は、電子計算機を発明し、その究極の目標である人工知能（万能の超人）を

正に完成させようとしているが、これを完成させる事が人類に課せられた究極の

使命ではではないかとも妄想するところではある。

尚、現行の主要な物理学理論と素光子説を対比して観た感想としては、或る前提

の元で理論を展開する過程で更に元の命題以上の問題が次々に生じる結果、論理

の展開が行き詰まった状態に陥っているのではないかと感じられる場合に、前提

を顧みる努力が敢えて行われていない様に思われる事が散見されるにつけ、学問

の最も基本的な指導原理を思い返して頂きたいという感想を付け加えさせて頂く。

　

　最後に、このアイデアが物理学の発展に多少でも寄与出来れば幸いである。

その為には、先ず、このアイデアの自己矛盾の有無のチェックや量子論やその他

の主要な物理理論との間の整合性の十分な検討や実験による検証が必須である。

　

　

＜参考図＞

＜図１；エネルギーを与えられた静止物質の速度ｖの運動状態の概念図＞

（例；加速器に於ける電場で裸の電子を加速し、光の衣を着た電子になる場合）

　エネルギー　 　　　静止物質Ｓ　　　　　速度ｖの物質Ｓの質量Ｍ＝Ｍ0／α

（E1＝ｎ1*ｅ) 　　　(Ｍ0＝ｎ0*ｍ0)　 　　Ｅ＝(１−α)*(ｎ0＋ｎ1)*ｅ

ｅ；素量子(素光子)の全エネルギー　　　　　　＋α*(ｎ0＋ｎ1)*ｅ

ｍ0；素量子の静止質量で,ｅ＝ｍ0*c^2　　　ｅ＝(１−α)*ｅ＋α*ｅ

ｎ0,ｎ1は素量子及び素光子の個数　　　　　α＝√(１−(ｖ／ｃ)^2)

　

（註）上図は電子の加速時に加えられた電磁場のエネルギーが物質化する様に描

いているが、実際は電子に捕捉された光が電子の周囲を光速で周回している描像

が正しいが、光が半束縛状態となり全体として電子の速度で運動している素量子

の状態として表現している図である。

　

＜図２；電磁波の素光子モデル＞

（註）波を構成している素光子は、波全体が光速で運動している為に、同心円状

に回転運動している状態では無く、静止した状態として観測されると考えられる。

　

　

＜参考文献＞

　

（Ａ）

電子からの光の放射時間の論理的導出

「ファインマン物理学�U 光 熱 波動」第２８刷 ｐ７８〜８１

Ｒ・Ｐ・ファインマン著、富山小太郎訳、岩波書店刊

　

（Ｂ）

ニュートン力学の範疇で、エネルギーと質量の等価式を求める方法

「間違いだらけの宇宙論＞Ｅ＝ｍｃ^2の導出方法」永田博一

http://www3.osk.3web.ne.jp/~redshift/proof1.html

　

上記の導出過程は、下記のファインマン物理学の記述を一部変更して引用。

「ファインマン物理学�T　力学」ｐ２２０〜２２１、坪井忠二訳、岩波書店刊

　

（Ｃ）

「ベクトルポテンシャルとは何ぞや？」前野昌弘

http://www.phys.u-ryukyu.ac.jp/~maeno/cgi-bin/pukiwiki/index.php?%A5%D9%A5%AF%A5%C8%A5%EB%A5%DD%A5%C6%A5%F3%A5%B7%A5%E3%A5%EB%A4%C8%A4%CF%B2%BF%A4%BE%A4%E4%A1%A9

　

（Ｄ）

超伝導現象及び原子核研究の参考サイト

　

（Ｄ）の（１）「将来的な研究は…。〜新たな超伝導状態〜」

東京大学 新領域創成科学科 物質系専攻 石井　究

http://yoshizawa.issp.u-tokyo.ac.jp/ishii/research.html

　

（Ｄ）の（２）「常温超伝導を目指して」

東京大学理学系研究科物理学専攻　内田　慎一

http://www.s.u-tokyo.ac.jp/ken/news-back/030117b.html

　

（Ｄ）の（３）「超伝導 マクロな量子現象」

早稲田大学理工学部物理学科 栗原 進

http://www.kh.phys.waseda.ac.jp/superconductivity@.html

　

（Ｄ）の（４）「核スピンで見通す物質の姿」

理化学研究所　応用原子核物理研究室　主任研究員 旭 耕一郎

http://www.riken.jp/r-world/info/release/news/2002/feb/index.html

　

（Ｄ）の（５）「高温超伝導の理解はどこまで進んだか？高温超伝導のやさしい

理解」東北大学大学院工学研究科応用物理学教授　小池洋二

http://www.apph.tohoku.ac.jp/low-temp-lab/materia.pdf

　

（Ｄ）の（６）「核子(陽子・中性子)スピンの起源に挑む」COMPASS国際共同研究

＜クォークスピンからグルーオンスピンへ＞

http://www.quark.kj.yamagata-u.ac.jp/compass/compass_intro_2006v3.pdf

　

（Ｄ）の（７）「陽子スピンの謎」に挑戦

http://www.rikenresearch.riken.jp/japan/research/50/

　

（Ｄ）の（８）「ニュートリノが明らかにする核子のスピン構造」

日本物理学会 平成 16 年3月29 日、京都大学理学部齊藤 直人

http://www.nucl.phys.titech.ac.jp/~neuspin/pdf/JPS2004-NuN-0.pdf

　

（Ｄ）の（９）「カイラル・クォーク・ソリトン模型と核子のスピン構造」

２００５年２月、東京工大

http://www.nucl.phys.titech.ac.jp/reports/Lecture/200502_wakamatsu/LECT1.PDF

　

（Ｄ）の（10）「原子核物理学」東京理科大学理学部第一部物理学科(2007年度)

http://www.rs.kagu.tus.ac.jp/beachey/NP/2007_NP_3_1.pdf

　

（Ｄ）の（11）「2005.5.16 現代物理学入門奇妙な原子核(エキゾチック原子核）

」大塚孝治

http://tkynt2.phys.s.u-tokyo.ac.jp/~otsuka/gendai_2005.pdf

　

（Ｄ）の（12）「常温核融合プロジェクト」

北海道大学院工学研究科量子エネルギー 水野忠彦

http://lenr-canr.org/acrobat/MizunoTjyouonkaku.pdf

　

（Ｄ）の（13）「未来を築く常温核融合」ジェト・ロスウェル著、大野順子訳

http://lenr-canr.org/acrobat/RothwellJmiraiokizu.pdf

　

（Ｄ）の（14）逆説の相対性理論＞光速度不変の謎

「６−７）光の媒質としてのエ−テルはどうなる？」

http://homepage3.nifty.com/gyakusou/sou1/kousoku/kousoku.html

　

（Ｄ）の（15）「常温核融合」

http://ja.wikipedia.org/wiki/%E5%B8%B8%E6%B8%A9%E6%A0%B8%E8%9E%8D%E5%90%88

　

（Ｅ）

クレイ数学研究所のミレニアム懸賞問題「７題難問ってなんですか？」

http://aomori.cool.ne.jp/akinee/other/ota/ota7.html

　

（Ｆ）

「ル・サージュの重力理論」Le Sage's theory of gravitation

”Le Sage gravity”でググル（インターネット検索エンジンでサイトを検索）と、

Le Sageの重力理論の多くの文献がヒットするが、国内文献は皆無に等しい。

http://en.wikipedia.org/wiki/Le_Sage's_theory_of_gravitation

　

「Lucrèce Newtonien」ル・サージュの重力理論の原典

http://bibliothek.bbaw.de/bibliothek-digital/digitalequellen/schriften/anzeige/index_html?band=03-nouv/1782&seite:int=0495

　

ル・サージュの重力理論の矛盾点の指摘

　

（１）「物理法則はいかにして発見されたか」ｐ４４〜４７

Ｒ・Ｐ・ファインマン著、江沢洋訳、ダイヤモンド社刊

　

（２）「重力を説明する古典力学的理論」＞掩蔽説

＜ル・サージュの重力理論の問題点＞

（�T）粒子の流れの掩蔽が起こるためには、粒子を物体がいくらか吸収しなけれ

ばならないことで、これは物体の温度の上昇を伴うと考えられる。

（�U）運動する物体間の重力を説明するためには粒子の速度は光速をこえなけれ

ばならない。

（�V）粒子の速度を高速だと仮定すると吸収による温度の上昇はさらに上昇しな

ければならない。

http://ja.wikipedia.org/wiki/%E9%87%8D%E5%8A%9B%E3%82%92%E8%AA%AC%E6%98%8E%E3%81%99%E3%82%8B%E5%8F%A4%E5%85%B8%E5%8A%9B%E5%AD%A6%E7%9A%84%E7%90%86%E8%AB%96

　

（Ｇ）

「ゲージ場の一般論」内山龍雄著

日本物理学会誌　第３５巻　第７号（１９８０）ｐ５６９〜５７５

http://www.geocities.jp/hodgestaroperator/uchiyama01.pdf

　

「一般ゲージ場論序説」内山龍雄著、岩波書店刊

　

（Ｈ）

「シュレーディンガーのジレンマと夢」長澤正雄著、森北出版株式会社刊

シュレーディンガー方程式に代わる確率過程論の一般向けの好書

内容見本；http://www.morikita.co.jp/soft/15341/

　

（Ｉ）

「力とは何か」菅野禮司著、丸善株式会社刊

力の本質を探求する一般向けの好書

　

（Ｊ）

アインシュタインの小論文

　

（Ｊ）の（１）「エーテルと相対論」アインシュタイン著、片山泰男訳

新しいエーテルに関するアインシュタインの１９２０年のライデン大学の講演録

http://home.catv.ne.jp/dd/pub/ether.html

　

（Ｊ）の（２）「物体の慣性は、そのエネルギー内容に依存するか」

アルバート・アインシュタイン、片山泰男訳

http://home.catv.ne.jp/dd/pub/inertia.html

　

（Ｊ）の（３）「質量エネルギーの等価性の初等的導出」

アルバート・アインシュタイン、片山泰男訳

http://home.catv.ne.jp/dd/pub/mass.html

　

（Ｊ）の（４）「E = M C^2」アルバート・アインシュタイン、片山泰男訳

http://home.catv.ne.jp/dd/pub/mass2.html

　

（Ｋ）

「時間と空間の物理学」高戸英順　e-meil；eijun@po.harenet.ne.jp

http://www1.harenet.ne.jp/~eijun/index.htm

　

（Ｌ）

宮沢弘成小論文

　

（Ｌ）の（１）「電子は質点か場か」宮沢弘成著

http://www7.ocn.ne.jp/~miyazaw1/papers/quantum.pdf

　

（Ｌ）の（２）「場と質点」宮沢弘成著

http://www7.ocn.ne.jp/~miyazaw1/papers/batosituten.pdf

　

（Ｌ）の（３）「質点と場と確率解釈」宮沢弘成著

http://www7.ocn.ne.jp/~miyazaw1/papers/probability.pdf

　

（Ｍ）

「量子力学」高林武彦著、保江邦夫編、海鳴社刊

量子力学の観測と解釈問題に関する著者の独自の見解

　

（Ｎ）

「アインシュタインの”神はサイコロを振らない”」ウィキペディアより

マックス・ボルンとの往復書簡での１９２６年１２月４日付の内容

原文：Die Quantenmechanik ist sehr achtunggebietend. Aber eine innere

Stimme sagt mir, daß das noch nicht der wahre Jakob ist. Die Theorie

liefert viel, aber dem Geheimnis des Alten bringt sie uns kaum näher.

Jedenfalls bin ich überzeugt, daß der Alte nicht würfelt.

　

直訳:量子力学にはとても尊敬の念を抱いています。

しかし内なる声が私に、その理論はまだ完璧ではないと言っています。

量子力学はとても有益なものではありますが、神の秘密には殆ど迫っていません。

少なくとも私には、神はサイコロを振らないという確信があるのです。

　

（Ｏ）

「ハイゼンベルクの顕微鏡」石井茂著、日経ＰＢ社刊

小澤正直博士による不確定性原理の不等式の誤りの指摘に纏わるエピソード。

　

（Ｐ）

ＥＰＲ論争の参考サイト

　

（Ｐ）の（１）「量子ポテンシャル理論と確率力学」大崎敏郎著

http://wwwndc.tokai-sc.jaea.go.jp/JNDC/ND-news/pdf76/No76-08.pdf

　

(Ｐ)の(２)「エヴェレットの多世界解釈 最後の量子力学」Toshifumi Sakaguchi

http://homepage2.nifty.com/qm/index_jap.html

　

（Ｑ）

ベクトル・ポテンシャル関連文献

　

（Ｑ）の(１)電子波で見る電磁界分布【ベクトルポテンシャルを感じる電子波】

外村彰

参考文献中の電子波の説明「電子は粒子として検出されるが，原子内部の電子や

速度の揃った電子の流れは，同時に波としても振る舞う．」

http://ieice.org/jpn/books/kaishikiji/200012/20001201-1.html

　

（Ｑ）の（２）「アハラノフ・ボーム効果とゲージ場」大貫義郎

http://nels.nii.ac.jp/els/110002075497.pdf?id=ART0002372146&type=pdf&lang=jp&host=cinii&order_no=&ppv_type=0&lang_sw=&no=1215125948&cp=

　

（Ｒ）

「量子力学３０講」初版　戸田盛和著　朝倉書店　Ｐ８５

　

（Ｓ）

鹿鳴館・理学部講座＞一般相対性理論と宇宙論＞電子の半径（付録１）

http://takaosuda.hp.infoseek.co.jp/homepage/relate/append1.html

　

（Ｔ）

「物体の速度と物質波の速度」山�ｱ 勝義　

http://ir.lib.hiroshima-u.ac.jp/metadb/up/81936204/RefdeBroglie.pdf

　

（Ｕ）

「複屈折」東京工業大学理工学研究科有機・高分子物質専攻　竹添・石川研究室

http://www.op.titech.ac.jp/lab/Take-Ishi/hirameki/biref.pdf

　

（Ｖ）

双曲幾何学関連資料

　

（Ｖ）の（１）「双曲幾何学」ウィキペディア

http://ja.wikipedia.org/wiki/%E5%8F%8C%E6%9B%B2%E5%B9%BE%E4%BD%95%E5%AD%A6

　

（Ｖ）の（２）「Ｎｅｗｔｏｎムック；ゼロと無限の科学」ニュートンプレス

p118〜121

　　　　＜ペンローズのインタビュー記事＞

宇宙の曲率に関する観測結果はそれほど明確のものではありません。

ビッグバンのなごりだと考えられている、マイクロ波背景放射のパターンという

ものがあります。

これを詳細に測定したＷＭＡＰ(ウイルキンソン−マイクロ波非等方性探査衛星）

の測定結果を見て、インフレーション理論を信奉する人たちは、「我々がずっと

主張してきたとおり、やはり宇宙は平らだ」というでしょう。

インフレーションは宇宙を平らにしたことになっているのですから。

確かにＷＭＡＰのデータには、宇宙が平らであることを支持する要素が含まれて

います。

しかし、スペクトルの低周波数域、すなわち宇宙を最大規模で観測したときにと

らえられる姿は、宇宙が平らであることを示していません。

私が考えるに、いちばんもっともらしい説明は、宇宙は全体として平らではない、

ということだと思います。

　

最近発表されたばかりのものですが、ガーザディアンというアルメニアの学者に

よる結果は、宇宙の曲率が負であることを示しています。

マイクロ波背景放射のパターンには、宇宙全体で多少の変動があります。

彼は、この変動のある領域がつくる形に注目しました。

この形が細長いのか、それとも丸い形をしているのかということを検討したので

す。

　

もし宇宙が平らか正の曲率を持つなら、この形はだいたい丸になります。

しかし、曲率が負だったとすると、この形はより引きのばされたものになるので

す。

彼は何年も前のＣＯＢＥ（宇宙背景放射探査衛星）のデータを検討し、その領域

の形が丸ではなく、もっと引きのばされていると結論しました。

彼はさらに高い精度をもつＢＯＯＭＥＲanＧ（ミリ波・銀河系外起源放射および

地球物理学の気球観測プロジェクト）とＷＭＡＰのデータについても検討して、

やはり同じ結論に到達したのです。

これは、宇宙の曲率は負であるという証拠であり、インフレーションを支持する

人々にとってはありがたくない発見です。

今や宇宙の曲率をめぐっては、このような相対立する解析結果のすべてを注意深

く見るべき段階にきています。

　

（３）「視覚の数理,4 双曲幾何学と非一様タイリング」全学自由研究ゼミナール

工学部計数工学科情報理工学系研究科数理情報学専攻杉原厚吉 2006-05-09

論文中の「図4.5. 双曲三角形によるタイリング．」は、下記（４）の有名な版画

と同じ作図法を用いたものである。

http://www.simplex.t.u-tokyo.ac.jp/~sugihara/lecturenotes/freezemi2006/section4.pdf

　

（Ｖ）の(4)≪円の極限IV(天国と地獄)≫　マウリッツ・コルネリス・エッシャー

http://www.japandesign.ne.jp/HTM/REPORT/art_review/34/big/08.html

　

（Ｗ）

ダークマター関連資料（ウィキペディア）

　

（Ｗ）の（１）「銀河の回転曲線問題」

http://ja.wikipedia.org/wiki/%E9%8A%80%E6%B2%B3%E3%81%AE%E5%9B%9E%E8%BB%A2%E6%9B%B2%E7%B7%9A%E5%95%8F%E9%A1%8C

　

（Ｗ）の（２）「暗黒物質」

http://ja.wikipedia.org/wiki/%E6%9A%97%E9%BB%92%E7%89%A9%E8%B3%AA

　

（Ｗ）の（３）「重力レンズ」

http://ja.wikipedia.org/wiki/%E9%87%8D%E5%8A%9B%E3%83%AC%E3%83%B3%E3%82%BA

　

（Ｗ）の（４）「パイオニア・アノマリー」

http://ja.wikipedia.org/wiki/%E3%83%91%E3%82%A4%E3%82%AA%E3%83%8B%E3%82%A2%E3%83%BB%E3%82%A2%E3%83%8E%E3%83%9E%E3%83%AA%E3%83%BC

　

（Ｗ）の（５）「修正ニュートン力学」

http://ja.wikipedia.org/wiki/%E4%BF%AE%E6%AD%A3%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E5%8A%9B%E5%AD%A6

　

（Ｗ）の（６）「Λ-CDMモデル」

http://ja.wikipedia.org/wiki/%CE%9B-CDM%E3%83%A2%E3%83%87%E3%83%AB

　

（Ｗ）の（７）「ダークエネルギー」

http://ja.wikipedia.org/wiki/%E3%83%80%E3%83%BC%E3%82%AF%E3%82%A8%E3%83%8D%E3%83%AB%E3%82%AE%E3%83%BC

　

（Ｘ）

宇宙論関連資料

　

（Ｘ）の（１）「宇宙定数問題」松原隆彦

http://www.a.phys.nagoya-u.ac.jp/~taka/lectures/cosmology/webfiles/cosmology-web/node66.html

　

（Ｘ）の（２）「Ouroborosとは」東京大学総合研究博物館ニュース　Ouroboros

第29号

”Ouroboros(ウロボロス)とは、自分の尾を噛んで環を作る蛇または竜で表現され

るシンボルをいいます。始めと終わりがない事から、自己の消尽と更新を繰り返

す永劫回帰や無限、真理と知識の合体、創造など幅広い意味を持っています。”

http://www.um.u-tokyo.ac.jp/museum/ouroboros/11_01/what.html

　

（Ｘ）の（３）「宇宙論的問題」片山泰男

http://home.catv.ne.jp/dd/pub/cosmo.html

　

（Ｙ）

「カシミール効果」ウィキペディア

http://ja.wikipedia.org/wiki/%E3%82%AB%E3%82%B7%E3%83%9F%E3%83%BC%E3%83%AB%E5%8A%B9%E6%9E%9C

　

（Ｚ）

素光子説に関するＹＡＨＯＯ掲示板

トップ > 科学 >　物理学 > 「どこえきえたか相対性理論。」

http://messages.yahoo.co.jp/bbs?.mm=GN&action=m&board=1835555&tid=a4ia43a4a8a4ada4a8a4bfa4abajbpc0admfdoc0a1a3&sid=1835555&mid=1&type=date&first=1